22.2: Force between two current-carrying wires

Consider two infinite parallel straight wires, a distance \(h\) apart, carrying upwards currents, \(I_{1}\) and \(I_{2}\), respectively, as illustrated in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Two parallel current-carrying wires will exert an attractive force on each other, if their currents are in the same direction.

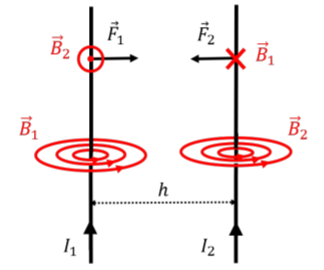
The first wire will create a magnetic field, \(\vec B_{1}\), in the shape of circles concentric with the wire. At the position of the second wire, the magnetic field \(B_{1}\) is into the page, and has a magnitude:

\[\begin{aligned} B_{1}=\frac{\mu_{0}I_{1}}{2\pi h} \end{aligned}\]

Since the second wire carries a current, \(I_{2}\), upwards, it will experience a magnetic force, \(\vec F_{2}\), from the magnetic field, \(B_{1}\), that is towards the left (as illustrated in Figure \(\PageIndex{1}\) and determined from the right-hand rule). The magnetic force, \(\vec F_{2}\), exerted on a section of length, \(l\), on the second wire has a magnitude given by:

\[\begin{aligned} F_{2}=I_{2}||\vec l\times\vec B_{1}||=I_{2}lB_{1}\frac{\mu_{0}I_{2}I_{1}l}{2\pi h} \end{aligned}\]

where we used the fact that the angle between \(\vec l\) and \(\vec B\) is \(90^{◦}\). We expect, from Newton’s Third Law, that an equal and opposite force should be exerted on the first wire. Indeed, the second wire will create a magnetic field, \(\vec B_{2}\), that is out of the page at the location of the first wire, with magnitude:

\[\begin{aligned} B_{2}=\frac{\mu_{0}I_{2}}{2\pi h} \end{aligned}\]

This leads to a magnetic force, \(\vec F_{1}\), exerted on the first wire, that points to the right (from the right-hand rule). On a section of length, \(l\), of the first wire, the magnetic force from the magnetic field, \(\vec B_{2}\), has magnitude:

\[\begin{aligned} F_{1}=I_{1}||\vec l\times\vec B_{2}||=I_{1}lB_{2}\frac{\mu_{0}I_{1}I_{2}}{2\pi h} \end{aligned}\]

which does indeed have the same magnitude as the force exerted on the second wire. Thus, when two parallel wires carry current in the same direction, they exert equal and opposite attractive forces on each other.

Exercise \(\PageIndex{1}\)

Figure \(\PageIndex{2}\): Two wires that carry current in opposite directions.

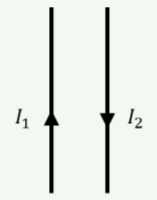
Two parallel wires carry current in opposite directions, as shown in Figure \(\PageIndex{2}\). What force do they exert on each other?

1. There will be no force, since the currents cancel.
2. There will be an attractive force between the wires.
3. There will be a repulsive force between the wires.

Answer

The attractive force between two wires used to be the basis for defining the Ampere, the S.I. (base) unit for electric current. Before 2019, the Ampere was defined to be “that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed one meter apart in vacuum, would produce between these conductors a force equal to \(2 × 10^{−17}\text{N}\) per meter of length”. Recently, the definition was updated to be based on defining the Coulomb in such a way that the elementary charge has a numerical value of \(e = 1.602 176 634 × 10^{−19}\text{C}\), and the Ampere corresponds to one Coulomb per second.

The force between two wires is a good system to understand how any physical quantity cannot depend on our choice of the right-hand to define cross-products. As mentioned in the previous chapter, any physical quantity, such as the direction of the force exerted on a wire, will always depend on two successive uses of the right hand. In this system, we first used the right-hand rule for axial vectors to determine the direction of the magnetic field from one of the wires. We then used the right-hand rule to determine the direction of the cross-product to determine the direction of the force on the other wire. You can verify that you get the same answer if you, instead, use your left-hand to define the direction of the magnetic field (which will be in the opposite direction), and then again for the cross-product. This also highlights that the magnetic field (and the electric field) is just a mathematical tool that we use to, ultimately, describe the motion of charges or compass needles.

Exercise \(\PageIndex{2}\)

When current is flowing in a straight cable, how to you expect the charges to be distributed radially through the cross-section of the cable?

1. Uniformly in radius (current density does not depend on \(r\)).
2. There will be an excess of positive charges on the outside of the cable.
3. There will be an excess of negative charges on the outside of the cable.

Answer