18.1: Overview
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Explain the relationship between the electric potential and the electric field
The relationship between electric potential and field is similar to that between gravitational potential and field in that the potential is a property of the field describing the action of the field upon an object (see ).
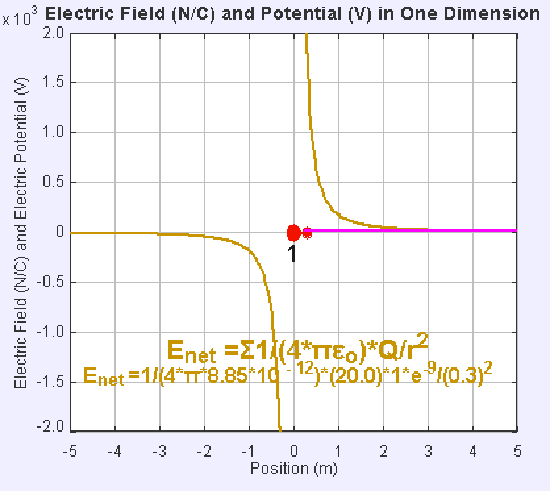
Electric field and potential in one dimension: The presence of an electric field around the static point charge (large red dot) creates a potential difference, causing the test charge (small red dot) to experience a force and move.
The electric field is like any other vector field—it exerts a force based on a stimulus, and has units of force times inverse stimulus. In the case of an electric field the stimulus is charge, and thus the units are NC-1. In other words, the electric field is a measure of force per unit charge.
The electric potential at a point is the quotient of the potential energy of any charged particle at that location divided by the charge of that particle. Its units are JC-1. Thus, the electric potential is a measure of energy per unit charge.
In terms of units, electric potential and charge are closely related. They share a common factor of inverse Coulombs (C-1), while force and energy only differ by a factor of distance (energy is the product of force times distance).
Thus, for a uniform field, the relationship between electric field (E), potential difference between points A and B (Δ), and distance between points A and B (d) is:
E=−Δϕd
The -1 coefficient arises from repulsion of positive charges: a positive charge will be pushed away from the positively charged plate, and towards a location of higher-voltage.
The above equation is an algebraic relationship for a uniform field. In a more pure sense, without assuming field uniformity, electric field is the gradient of the electric potential in the direction of x:
Ex=−dVdx
This can be derived from basic principles. Given that ∆P=W (change in the energy of a charge equals work done on that charge), an application of the law of conservation of energy, we can replace ∆P and W with other terms. ∆P can be substituted for its definition as the product of charge (q) and the differential of potential (dV). We can then replace W with its definition as the product of q, electric field (E), and the differential of distance in the x direction (dx):
qdV=−qExdx
Dividing both sides of the equation by q yields the previous equation.
Electric Potential Energy and Potential Difference
Electric potential energy results from forces between charges; potential difference is the energy needed to move a charge from point A to B.
learning objectives
- Calculate the potential energy between the charges
Electric potential energy is a type of potential energy that results from Coulomb forces. It is measured in joules and depends on the positioning of charged particles relative to one another, as well as the magnitude of their respective charges.
The potential energy (UE) between charges q and Q can be calculated as a function of distance between the charges (r):
UE(r)=qQ4πϵ0r
If there are three or more charges, the above formula can be modified so that the potential energies between all charges are summed. Consider, for example, the case involving charges Q1, Q2 and Q3:
UE=14πϵ0r(Q1Q2r12+Q2Q3r23+Q1Q3r13)
In this example, r12 represents the distance between Q1 and Q2, r23 represents the distance between Q2 and Q3, and r13represents the distance between Q1 and Q3. The above formula can be modified for any number of charges.
Potential Difference
Potential difference, or voltage, is the difference in electric potential energy between two points. It is denoted by ∆V and has units of volts, or joules per Coulomb.
Electric Potential Difference: A brief overview of electric potential difference and electric potential energy for beginning physics students.
Voltage denotes the work per unit charge that must be done against a static electric field to move a charge from one point to another. It may represent a source of energy, or lost, stored or used energy. Voltage also is defined such that negative charges are pulled towards higher voltages, while positive charges move towards lower voltages. Thus, current in wires flows from higher to lower voltages.
Potential difference is independent of path taken from one point to another, and may be measured by any of a number of instruments. These include the voltmeter, the potentiometer, and the oscilloscope. It is most typically measured in circuits, and in such situations can be calculated using Ohm ‘s Law, which will be covered in a later atom.
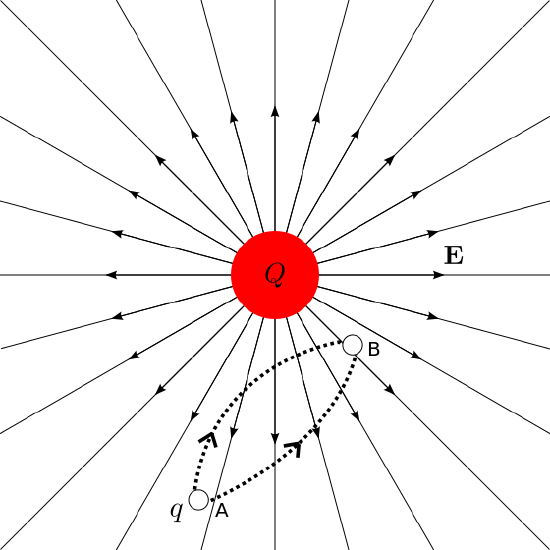
Potential difference in a static field: When a charge q moves from point A to point B, the potential difference is independent of path taken.
Electric Field and Changing Electric Potential
Electric field is the gradient of potential, which depends inversely upon distance of a given point of interest from a charge.
learning objectives
- Calculate the electric potential created by a charge distribution of constant value
Any charge will create a vector field around itself (known as an electric field ). Electric field is the gradient of potential, which depends inversely upon distance of a given point of interest from a charge. Placing a second charge in the system (a “test charge”) results in the two charges experiencing a force (the field’s units are Newtons, a measure of force per Coulomb), causing the charges to move relative to one another. It is easiest to model interactions between two charges such that one is considered stationary while the test charge moves.
As the test charge moves, the potential between it and another charge changes, as does the electric field. The relationship between potential and field (E) is a differential: electric field is the gradient of potential (V) in the x direction. This can be represented as:
Ex=−dVdx
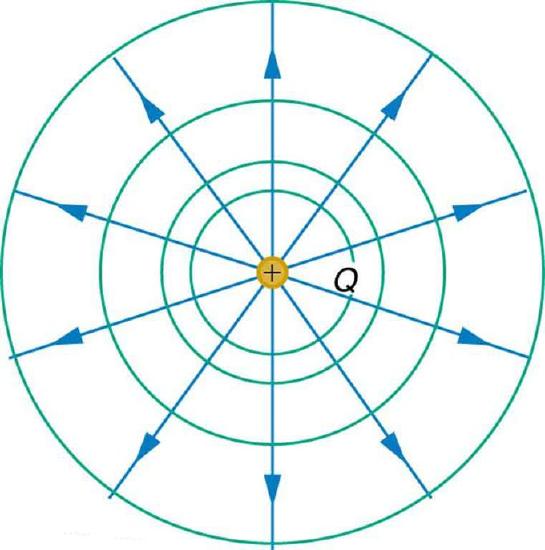
Equipotential Lines: An isolated point charge Q with its electric field lines (blue) and equipotential lines (green)
Thus, as the test charge is moved in the x direction, the rate of the its change in potential is the value of the electric field.
The instant before the test charge moves, its potential energy is at a maximum, and its kinetic energy is 0. For any charge of constant value (Q), the potential at a certain distance from it (r) can be calculated from the following equation:
VE=14πϵ0Qr
where ε0 is the electric constant, otherwise known as permittivity of free space. Moving towards and away from the charge results in change of potential; the relationship between distance and potential is inverse.
For one point charge, potential will be constant for all points a certain radial distance away. Multiple points of the same potential are known as equipotential. In the case of fields created by a single point charge, all points on any circle centered around the point charge will be equipotential, as illustrated in.
shows that when multiple charges create a field, the equipotential lines become irregularly shaped. This is due to the fact that the fields created by each charge overlap, thus potential is increased at any point relative to that which would have arisen from one or the other charge.
Potentials and Charged Conductors
Electric potential within a charged conductor is equal to zero, but can be calculated as a nonzero value outside of a charged conductor.
learning objectives
- Determine the electric potential within and outside a charged conductor
When a conductor becomes charged, that charge distributes across its surface until electrostatic equilibrium is reached. Its surface is equipotential.
All points within a charged conductor experience an electric field of 0. This is because field lines from charges on the surface of the conductor oppose one another equally. However, having the electric field equal to zero at all points within a conductor, the electric potential within a conductor is not necessarily equal to zero for all points within that same conductor. This can be proven by relating electric field and potential.
Electrical Charge at a Sharp Point of a Conductor: Repulsive forces towards the more sharply curved surface on the right aim more outward than along the surface of the conductor.
Given that work is the difference in final and initial potential energies (∆U), we can relate this difference to the dot product of force at every infinitesimal distance l along the path between the points within the conductor:
\Delta \mathrm { U } = - \int _ { \mathrm { i } } ^ { f } \vec { \mathrm { F } } \cdot \mathrm { d } \vec { }
This is the equation for work, with ∆U substituted in place of W. Rewriting U as the product of charge (q) and potential difference (V), and force as the product of charge and electric field (E), we can assert:
Δ(qV)=−∫fi(qE)⋅d→l
Dividing both sides by the common term of q, we simplify the equation to:
ΔV=−∫fi→E⋅d→l
Finally we derive the equation:
dV=−→E⋅d→l=0
Thus we can conclude that, given that the electric field is constantly 0 for any location within the charged conductor, the potential difference in that same volume needs to be constant and equal to 0.
On the other hand, for points outside a conductor, potential is nonzero and can be defined by the very same equation, according to field and distance from the conductor.
Uniform Electric Field
An electric field that is uniform is one that reaches the unattainable consistency of being constant throughout.
learning objectives
- Describe properties and approximations of the uniform electric field
A uniform field is that in which the electric field is constant throughout. Just like the so-called “frictionless surface” in mechanics, the uniform field is an ideal but unreal situation that makes for simpler calculations. Equations involving non-uniform electric fields require use of differential calculus.
Uniformity in an electric field can be approximated by placing two conducting plates parallel to one another and creating a potential difference between them. In such a case there will be slight variations in the field near its edges, but it will be approximately constant throughout every other area.
The equation for magnitude of a uniform electric field is:
E=−Δϕd
where E is the field, Δ is the potential difference between the plates, and d is the distance between the plates. The coefficient of -1 arises from the fact that positive charges repel, and thus a positive charge will be pushed away from the positive plate and in a direction opposite that of the increasing voltage.
Uniformity of an electric field allows for simple calculation of work performed when a test charge is moved across it. For the case of a positive charge q to be moved from a point A with a certain potential (V1) to a point B with another potential (V2), that equation is:
W=−q(V2−V1)
The difference (V2-V1) can also be represented as ∆V or VAB. In uniform fields it is also simple to relate ∆V to field strength and distance (d) between points A and B:
VAB=Ed
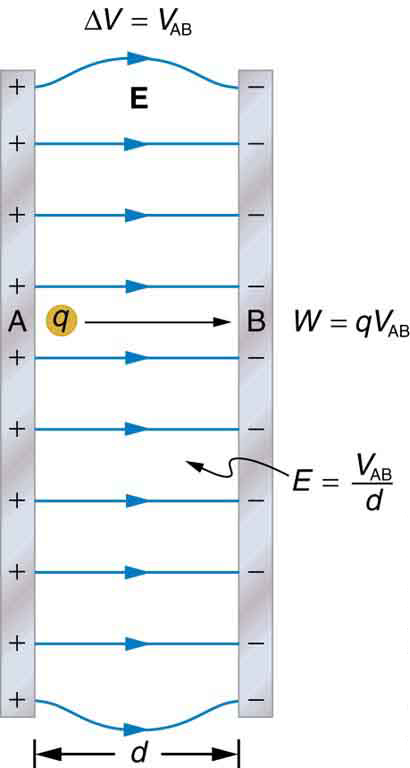
Relationships within a uniform electric field: In this image, Work (W), field strength (E), and potential difference (∆V) are defined for points A and B within the constructs of a uniform potential field between the positive and negative plates.
Energy Conservation
Energy is conserved in the movement of a charged particle through an electric field, as it is in every other physical situation.
learning objectives
- Formulate energy conservation principle for a charged particle in an electric field
Energy is conserved in the movement of a charged particle through an electric field, as it is in every other physical situation. This phenomenon can be expressed as the equality of summed kinetic (Ekin) and electric potential (Eel) energies:
(Ekin+Eel) initial =(Ekin+Eel)final
Given a stationary test charge in a certain location, an applied electric field will cause the charge to move to one end or the other, depending on the charge (positive test charges will move in the direction of the field; negative charges will move in the opposite direction). In all cases, a charge will naturally move from an area of higher potential energy to an area of lower potential energy.
At the instant at which the field is applied, the motionless test charge has 0 kinetic energy, and its electric potential energy is at a maximum. After that moment, the charge accelerates, and its kinetic energy (from motion) increases as its potential energy decreases. Throughout this time, the sum of potential and kinetic energies remains constant.
Another way to express the previous equation is:
(12mv2+U) initial =(12mv2+U)final
where m and v are the mass and velocity of the electron, respectively, and U is the electric potential energy. U can be calculated as follows:
U=q0V=kq0qr
where V is the potential difference, k is a constant, q0 is a test charge, q is another charge, and r is the distance between the charges.
The terms involved in the formula for conservation of energy can be rewritten in many ways, but all expressions are based on the simple premise of equating the initial and final sums of kinetic and potential energy.
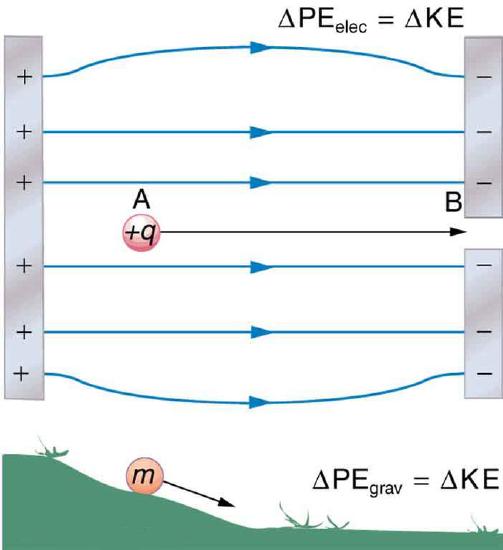
Similarities Between Activity of Gravitational and Electric Fields on an Object: The charge, +q, is moved down the electric field in the same way that the object, m, is moved down the hill. In both instances, the particle in motion goes from a higher to a lower potential energy state.
The Electron-Volt
The electron volt is a unit of energy useful in the physics of elementary charges and electricity.
learning objectives
- Convert between electron volts and SI units of energy
Overview
The electron volt, symbolized as eV and sometimes written as electronvolt, is a unit of energy useful in the physics of elementary charges and electricity.
The electron volt is defined as the amount of energy gained or lost by the charge of an electron moved across a one-volt electric potential difference. As such, it is equal to the product of one volt (1 J/C) and one elementary charge, giving it a value in joules approximately equal to 1.602×10-19 J.
Not an SI unit in itself, the electron volt became useful through experimentation. Scientists working with electrostatic particle accelerators commonly used the relationship between energy (E), charge (q), and potential difference (V) in their work:
E=qV
All calculations of energy from the above equation were quantized as multiples of the elementary charge, q, for a given voltage, and thus arose the common usage of the electron volt as a unit of measurement.
Momentum
Both electron volts and momentum are measures of energy, and the two are related in high-energy physics. Applying a potential difference to an electron gives it energy, which manifests itself in motion of the electron through it. Given that the electron has both mass and velocity, it has momentum. Dividing electron volts by a constant with units of velocity results in a momentum.
Mass
Given that mass is equivalent to energy, the electron volt can measure mass. In particle physics, the equation E=mc2 can be rearranged to solve for mass:
m=Ec2
Wavelength
The energy E, frequency v, and wavelength λ of a photon are related by
E(eV)=hv=hcλ
where h is the Planck constant and c is the speed of light. Thus, a photon with a wavelength of 532 nm (green light) would have an energy of approximately 2.33 eV. Similarly, 1 eV would correspond to an infrared photon of wavelength 1240 nm, and so on.

Energy of Photons in the Visible Spectrum: Relationship between wavelength and energy expressed in electron volts.
Temperature
In plasma physics, the electron volt can be used as a unit of temperature. To convert to Kelvins, simply divide the value of 1 eV (in Joules) by the Boltzmann constant (1.3806505(24)×10-23 J/K).
Dipole Moments
The electric dipole moment is a measure of polarity in a system.
learning objectives
- Relate the electric dipole moment to the polarity in a system
The electric dipole moment is a measure of polarity, which is the separation of positive and negative charges in a system. It is measured in units of Coulomb-meters (C m). There are many different types of dipole moments, including electric dipole moments, magnetic dipole moments, and topological dipole moments.
Among the subset of electric dipole moments are transition dipole moments, molecular dipole moments, bond dipole moments, and electron electric dipole moments. For the purposes of this atom we will focus on a broad overview of electric dipole moment in static situations.
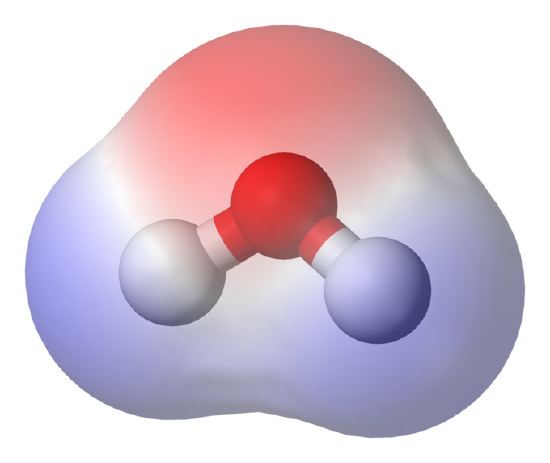
Molecular Dipole Moment in Water: This water (H2O) molecule has a high density of electrons (denoted by the red shading) near the red O atom. Closer to the white H atoms, there is a low density of electrons. Therefore, the molecule is is a dipole, with negativity near the O and positivity closer to the H atoms.
Definition
Fundamentally, for the case of point charges with values +q and -q, an electric dipole moment (p) can be defined as the vector product of the charges and the displacement vector d:
p=qd
The displacement vector is the vector with a magnitude equal to the distance between the charges and a direction pointing from the negative charge to the positive charge. It is essentially interchangeable with the “radius” variable in many other equations (such as those determining gravitational and electrostatic forces ), except that it includes the factor of direction.
Torque
All dipoles will experience a torsional force, or torque, when they are placed in external electric fields. This torque rotates the dipole to align it with the field. It is brought on by the need to minimize potential energy. Torque (τ) can be calculated as the cross product of the electric dipole moment and the electric field (E), assuming that E is spatially uniform:
τ=p×E
Key Points
- The electric field is a measure of force per unit charge; the electric potential is a measure of energy per unit charge.
- For a uniform field, the relationship between electric field (E), potential difference between points A and B (Δ), and distance between points A and B (d) is: E=−Δϕd If the field is not uniform, calculus is required to solve.
- Potential is a property of the field that describes the action of the field upon an object.
- Electric potential energy is a type of potential energy that results from Coulomb forces. The potential energy (UE) between charges q and Q can be calculated as a function of distance between the charges (r): UE(r)=qQ4πϵ0r.
- The formula for potential energy can be modified for potential between many charges, so long as the interactions of each charge with every other charge in the system are considered. For example, potential between three charges can be solved using the following formula: UE=14πϵ0r(Q1Q2r12+Q2Q3r23+Q1Q3r13).
- Potential difference, or voltage, is the difference in electric potential energy between two points. It is denoted by ∆V and has units of volts, or joules per Coulomb.
- For any charge of constant value (Q), the potential (VE) at a certain distance from it (r) can be calculated from the equation: VE=14πϵ0Qr Where ε0 is the electric constant, otherwise known as permittivity of free space.
- For one point charge, potential will be constant for all points a certain radial distance away. Multiple points of the same potential are known as equipotential.
- When multiple charges create a field, the equipotential lines become irregularly shaped. This is because the fields created by each charge overlap, thus the potential is increased at any point relative to that which would have arisen from one or the other charge.
- Electric potential (∆V) and field (E) are related according to the integral: ΔV=−∫fi→E⋅d→l where l is the distance between two points between which the potential difference is being found.
- Given that the electric field is constantly 0 for any location within the charged conductor, it is impossible for potential difference in that same volume to have any value other than 0.
- For points outside a conductor, potential is nonzero and can be calculated according to field and distance from the conductor.
- The uniform electric field is an approximation that makes for simple calculations that don’t require differential calculus. Every field will have at least some irregularity, although some can be very nearly uniform.
- The equation for magnitude of a uniform electric field is: E=−Δϕd where E is the field, Δ is the potential difference between the plates, and d is the distance between the plates.
- For the case of a positive charge q to be moved from a point A with a certain potential (V1) to a point B with another potential (V2), that equation is: W=−q(V2−V1)The difference (V2-V1) can also be represented as ∆V or VAB.
- In uniform fields it is also simple to calculate potential difference: VAB=Ed In this case, field strength is E, and distance between points A and B is d.
- Given a stationary test charge in a certain location, an applied electric field will cause the charge to move to one end or the other, depending on the charge.
- Positive test charges will move in the direction of the field; negative charges will move in the opposite direction.
- At the instant at which the field is applied, the motionless test charge has 0 kinetic energy, and its electric potential energy is at a maximum. Then, the charge accelerates, and its kinetic energy (from motion) increases as its potential energy decreases.The sum of energies is always constant.
- The formula illustrating conservation of energy can be written in many ways, but all expressions are based on the simple premise of equating the initial and final sums of kinetic and potential energy.
- The electron volt is defined as the amount of energy gained or lost by the charge of an electron moved across a one-volt electric potential difference. Its value is approximately equal to 1.602×10-19 J.
- The electron volt became useful through experimentation. Scientists working with electrostatic particle accelerators commonly used the relationship between energy (E), charge (q), and potential difference (V) in their work. This relationship is: E=qV.
- As an energy, the electron volt can be used in many calculations, including momentum, mass, wavelength, and temperature.
- Electric dipole moments are used to measure the separation of positive and negative charges ( polarity ) in a system. They are measured in units of Coulomb-meters (C m).
- For point charges with values +q and -q, electric dipole moment (p) can be defined as: p=qd where q represents the charges and d represents the displacement vector. The displacement vector has a magnitude of the distance between the charges and a direction from the negative to the positive charge.
- All dipoles will experience a torque that rotates the dipole to align it with an electric field. This torque can be calculated as the cross product of the electric dipole moment and the electric field.
Key Terms
- electric field: A region of space around a charged particle, or between two voltages; it exerts a force on charged objects in its vicinity.
- electric potential: The potential energy per unit charge at a point in a static electric field; voltage.
- coulomb: In the International System of Units, the derived unit of electric charge; the amount of electric charge carried by a current of 1 ampere flowing for 1 second. Symbol: C
- potential energy: The energy an object has because of its position (in a gravitational or electric field) or its condition (as a stretched or compressed spring, as a chemical reactant, or by having rest mass)
- equipotential: A region whose every point has the same potential.
- radial: Moving along a radius.
- electric field: A region of space around a charged particle, or between two voltages; it exerts a force on charged objects in its vicinity.
- work: A measure of energy expended in moving an object; most commonly, force times displacement. No work is done if the object does not move.
- potential difference: The difference in potential energy between two points in an electric field; the difference in charge between two points in an electrical circuit; voltage.
- kinetic energy: The energy possessed by an object because of its motion, equal to one half the mass of the body times the square of its velocity.
- particle accelerator: A device that accelerates electrically charged particles to extremely high speeds, for the purpose of inducing high-energy reactions or producing high-energy radiation.
- electron volt: A unit for measuring the energy of subatomic particles; the energy equal to that attained by an electron moving through a potential difference of one volt. Equivalent to 1.6022 x 10-19 joules.
- dipole moment: The vector product of the charge on either pole of a dipole and the distance separating them.
- vector: A directed quantity, one with both magnitude and direction; the between two points.
- torque: A rotational or twisting effect of a force; (SI unit newton-meter or Nm; imperial unit foot-pound or ft-lb)
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- electric field. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electric_field. License: CC BY-SA: Attribution-ShareAlike
- Electric potential. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_potential. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_field. License: CC BY-SA: Attribution-ShareAlike
- electric potential. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electric_potential. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Voltage. License: CC BY-SA: Attribution-ShareAlike
- Electric potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_potential_energy. License: CC BY-SA: Attribution-ShareAlike
- potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/potential%20energy. License: CC BY-SA: Attribution-ShareAlike
- coulomb. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/coulomb. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- radial. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/radial. License: CC BY-SA: Attribution-ShareAlike
- equipotential. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/equipotential. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- electric potential. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electric_potential. License: CC BY-SA: Attribution-ShareAlike
- electric field. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electric_field. License: CC BY-SA: Attribution-ShareAlike
- Electric potential. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_potential. License: CC BY-SA: Attribution-ShareAlike
- work. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/work. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- OpenStax College, College Physics. December 28, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42317/latest/?collection=col11406/latest. License: CC BY: Attribution
- potential difference. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/potential_difference. License: CC BY-SA: Attribution-ShareAlike
- electric field. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/electric_field. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_field. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Electric Potential in a Uniform Electric Field. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42326/latest/. License: CC BY: Attribution
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- OpenStax College, College Physics. December 28, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42317/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, Electric Potential in a Uniform Electric Field. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42326/latest/. License: CC BY: Attribution
- Electric potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_potential_energy. License: CC BY-SA: Attribution-ShareAlike
- potential difference. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/potential_difference. License: CC BY-SA: Attribution-ShareAlike
- kinetic energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/kinetic%20energy. License: CC BY-SA: Attribution-ShareAlike
- potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/potential%20energy. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- OpenStax College, College Physics. December 28, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42317/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, Electric Potential in a Uniform Electric Field. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42326/latest/. License: CC BY: Attribution
- OpenStax College, Electric Potential Energy: Potential Difference. January 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42324/latest/. License: CC BY: Attribution
- potential difference. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/potential_difference. License: CC BY-SA: Attribution-ShareAlike
- Electronvolt. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electronvolt. License: CC BY-SA: Attribution-ShareAlike
- electron volt. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electron_volt. License: CC BY-SA: Attribution-ShareAlike
- particle accelerator. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/particle_accelerator. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- OpenStax College, College Physics. December 28, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42317/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, Electric Potential in a Uniform Electric Field. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42326/latest/. License: CC BY: Attribution
- OpenStax College, Electric Potential Energy: Potential Difference. January 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42324/latest/. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/7f/Colors_in_eV.svg/605px-Colors_in_eV.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Electric dipole moment. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Electric_dipole_moment. License: CC BY-SA: Attribution-ShareAlike
- torque. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/torque. License: CC BY-SA: Attribution-ShareAlike
- vector. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/vector. License: CC BY-SA: Attribution-ShareAlike
- dipole moment. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/dipole_moment. License: CC BY-SA: Attribution-ShareAlike
- Electric field. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electric_field.gif. License: CC BY-SA: Attribution-ShareAlike
- Electrostatic definition of voltage. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Electrostatic_definition_of_voltage.svg. License: CC BY-SA: Attribution-ShareAlike
- Electric Potential Difference. Located at: http://www.youtube.com/watch?v=jjwwb2yfytk. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Equipotential Lines. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42331/latest/. License: CC BY: Attribution
- OpenStax College, College Physics. December 28, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42317/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, Electric Potential in a Uniform Electric Field. January 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42326/latest/. License: CC BY: Attribution
- OpenStax College, Electric Potential Energy: Potential Difference. January 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42324/latest/. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/7f/Colors_in_eV.svg/605px-Colors_in_eV.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Water-elpot-transparent-3D-balls. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Water-elpot-transparent-3D-balls.png. License: CC BY-SA: Attribution-ShareAlike



