29.3: Atomic Physics and Quantum Mechanics
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Explain relationship between the wave nature of matter and the quantization of energy levels in bound systems
To consider why wave nature of matter in bound systems leads to quantization, let’s consider an example in classical mechanics. We will look at a basic string “instrument” (a string pulled tight and fixed at both ends). If a string was free and not attached to anything, we know that it could oscillate at any driven frequency. However, the string in this example (with fixed ends and specific length) can only produce a very specific set of pitches because only waves of a certain wavelength can “fit” on the string of a given length with fixed ends. Once the string becomes a “bound system” with specific boundary restrictions, it allows waves with only a discrete set of frequencies.
This is the exact mechanism that causes quantization in atoms. The wave nature of matter is responsible for the quantization of energy levels in bound systems. Just like a free string, the matter wave of a free electron can have any wavelength, determined by its momentum. However, once an electron is “bound” by a Coulomb potential of a nucleus, it can no longer have an arbitrary wavelength as the wave needs to satisfy a certain boundary condition. Only those states where matter interferes constructively (leading to standing waves) exist, or are “allowed” (see illustration in.
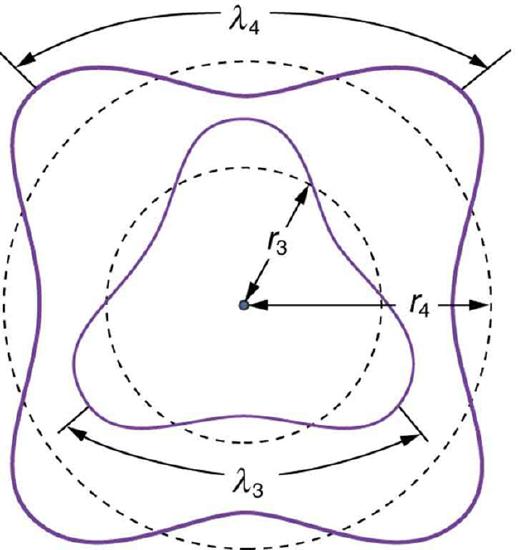
Fig 2: The third and fourth allowed circular orbits have three and four wavelengths, respectively, in their circumferences.
Assuming that an integral multiple of the electron’s wavelength equals the circumference of the orbit, we have:
nλn=2πrn(n=1,2,3,…)
Substituting λ=hmev, this becomes:
nhmev=2πrn
The angular momentum is L=mevr, therefore we obtain the quantization of angular momentum:
L=mevrn=nh2π(n=1,2,3,…)
As previously discussed, Bohr was forced to hypothesize this as the rule for allowed orbits. We now realize this as a condition for constructive interference of an electron in a (bound) circular orbit.
Photon Interactions and Pair Production
Pair production refers to the creation of an elementary particle and its antiparticle, usually when a photon interacts with a nucleus.
learning objectives
- Describe process of pair production as the result of photon interaction with nucleus
Below is an illustration of pair production, which refers to the creation of an elementary particle and its antiparticle, usually when a photon interacts with a nucleus. For example, an electron and its antiparticle, the positron, may be created. This is allowed, provided there is enough energy available to create the pair (i.e., the total rest mass energy of the two particles) and that the situation allows both energy and momentum to be conserved. Some other conserved quantum numbers such as angular momentum, electric charge, etc., must sum to zero as well. The probability of pair production in photon-matter interactions increases with increasing photon energy, and also increases with atomic number (Z) of the nucleus approximately as Z2.
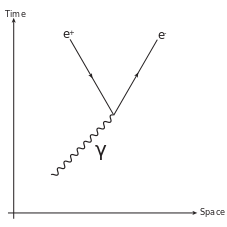
Pair Production: Feynman diagram for pair production. A photon decays into an electron-positron pair.
γ+γ→e−+e+
In nuclear physics, this reaction occurs when a high-energy photon ( gamma rays ) interacts with a nucleus. The energy of this photon can be converted into mass through Einstein’s equation E=mc2 where E is energy, mm is mass and c is the speed of light. The photon must have enough energy to create the mass of an electron plus a positron. The mass of an electron is 9.11⋅10−31 kg (equivalent to 0.511 MeV in energy), the same as a positron.
Without a nucleus to absorb momentum, a photon decaying into electron-positron pair (or other pairs for that matter) can never conserve energy and momentum simultaneously. The nucleus in the process carries away (or provides) access momentum.
The reverse process is also possible. The electron and positron can annihilate and produce two 0.511 MeV gamma photons. If all three gamma rays, the original with its energy reduced by 1.022 MeV and the two annihilation gamma rays, are detected simultaneously, then a full energy peak is observed.
These interactions were first observed in Patrick Blackett’s counter-controlled cloud chamber, leading him to receive the 1948 Nobel Prize in Physics.
Key Points
- Strings in musical instruments (guitar, for example) can only produce a very specific set of pitches because only waves of a certain wavelength can “fit” on the string of a given length with fixed ends.
- Similarly, once an electron is bound by a Coulomb potential of a nucleus, it no longer can have any arbitrary wavelength because the wave should satisfy a certain boundary condition.
- Bohr’s quantization assumption can be derived from the condition for constructive intereference of an electron matter wave in a circular orbit.
- The probability of pair production in photon -matter interactions increases with increasing photon energy, and also increases with atomic number of the nucleus approximately as Z.
- Energy and momentum should be conserved through the pair production process. Some other conserved quantum numbers such as angular momentum, electric charge, etc., must sum to zero as well.
- Nucleus is needed in the pair production of electron and positron to satisfy the energy and momentum conservation laws.
Key Terms
- quantization: The process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as quantum mechanics.
- angular momentum: A vector quantity describing an object in circular motion; its magnitude is equal to the momentum of the particle, and the direction is perpendicular to the plane of its circular motion.
- matter wave: A concept reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie.
- gamma ray: A very high frequency (and therefore very high energy) electromagnetic radiation emitted as a consequence of radioactivity.
- positron: The antimatter equivalent of an electron, having the same mass but a positive charge.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, The Wave Nature of Matter Causes Quantization. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42606/latest/. License: CC BY: Attribution
- quantization. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/quantization. License: CC BY-SA: Attribution-ShareAlike
- matter wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/matter%20wave. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/angular-momentum. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Wave Nature of Matter Causes Quantization. January 29, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42606/latest/. License: CC BY: Attribution
- Pair production. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pair_production. License: CC BY-SA: Attribution-ShareAlike
- positron. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/positron. License: CC BY-SA: Attribution-ShareAlike
- gamma ray. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/gamma_ray. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Wave Nature of Matter Causes Quantization. January 29, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42606/latest/. License: CC BY: Attribution
- Pair production. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pair_production. License: CC BY: Attribution

