5.9: Angular vs. Linear Quantities
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe properties characteristic to angular velocity and angular momentum
Linear motion is motion in a straight line. This type of motion has several familiar vector quantities associated with it, including linear velocity and momentum. These vector quantities each have a magnitude (a scalar, or number) and direction associated with them. Similarly, circular motion is motion in a circle. It has the same set of vector quantities associated with it, including angular velocity and angular momentum.
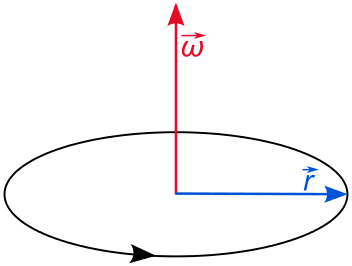
Angular velocity diagram: A vector diagram illustrating circular motion. The blue vector connects the origin (center) of the motion to the position of the particle. The red vector is the angular velocity vector, pointing perpendicular to the plane of motion and with magnitude equal to the instantaneous velocity. File:Angular velocity.svg - Wikipedia, the free encyclopedia. Provided by: Wikipedia. Located at: en.Wikipedia.org/w/index.php?title=File:Angular_velocity.svg&page=1. License: CC BY-SA: Attribution-ShareAlike
Imagine a particle moving in a circle around a point at a constant speed. We will call that point the origin. At any instant in time, the particle is moving in a particular straight-line direction with that speed. In the next instant, the particle has the same speed, but the direction of its velocity has changed.
We recall from our study of linear velocity that a change in the direction of the velocity vector, is a change in velocity and a change in velocity is acceleration. However, we can define an angular momentum vector which is constant throughout this motion. The angular velocity has a direction perpendicular to the plane of circular motion, just like a bike axle points perpendicularly to the rotating wheel. This direction never changes as the object moves in its circle. The magnitude of the angular momentum is equal to the rate at which the angle of the particle advances:
ω=dϕdt
Note that there are two vectors that are perpendicular to any plane. For example, imagine a vector pointing into your table and the opposite one pointing out of it. To remove this ambiguity, the convention in physics is to use the right hand rule: curl the fingers of your right hand in the direction of the circular motion, and your thumb will point toward the direction of the angular velocity and momentum vectors.

Right hand rule: When determining the direction of an angular vector, use the right hand rule: curl the fingers of your right hand in the direction of the circular motion and your thumb points in the vector direction. File:Right-hand grip rule.svg - Wikipedia, the free encyclopedia. Provided by: Wikipedia. Located at: en.Wikipedia.org/w/index.php?title=File:Right-hand_grip_rule.svg&page=1. License: CC BY-SA: Attribution-ShareAlike
The units of angular velocity are radians per second. Radian describes the plane angle subtended by a circular arc as the length of the arc divided by the radius of the arc. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. More generally, the magnitude in radians of such a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, θ=sr, where θ is the subtended angle in radians, s is arc length, and r is radius.
Thus, while the object moves in a circle at constant speed, it undergoes constant linear acceleration to keep it moving in a circle. However, it’s angular velocity is constant since it continually sweeps out a constant arc length per unit time. Constant angular velocity in a circle is known as uniform circular motion.
Just as there is an angular version of velocity, so too is there an angular version of acceleration. When the object is going around a circle but its speed is changing, the object is undergoing angular acceleration. Just like with linear acceleration, angular acceleration is a change in the angular velocity vector. This change could be a change in the speed of the object or in the direction. Angular velocity can be clockwise or counterclockwise.
Key Points
- The direction of angular quantity vectors points perpendicular to the plane of the motion. You can determine this direction using the right hand rule.
- The direction of linear quantities such as velocity and momentum change as an object moves in a circle. We can instead define angular versions of these quantities which are constant throughout the circular motion.
- The units of angular quantities are per radian, a measurement of angle, rather than per linear distance (e.g. meter).
Key Terms
- vector: A directed quantity, one with both magnitude and direction; the between two points.
- angular momentum: A vector quantity describing an object in circular motion; its magnitude is equal to the momentum of the particle, and the direction is perpendicular to the plane of its circular motion.
- angular velocity: A vector quantity describing an object in circular motion; its magnitude is equal to the speed of the particle and the direction is perpendicular to the plane of its circular motion.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Right hand rule. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Right_hand_rule. License: CC BY-SA: Attribution-ShareAlike
- Angular velocity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angular_velocity. License: CC BY-SA: Attribution-ShareAlike
- Radians. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Radians. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/angular-momentum. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/angular-velocity. License: CC BY-SA: Attribution-ShareAlike
- vector. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/vector. License: CC BY-SA: Attribution-ShareAlike

