2.3: Dynamics
( \newcommand{\kernel}{\mathrm{null}\,}\)
Concepts and Principles
Newton's First Law
Dynamics is the study of the cause of motion, or more precisely the cause of changes in motion. In the late 1600’s Isaac Newton hypothesized that motion does not require a cause, rather changes in motion require causes. An object experiences a change in motion only when it interacts with some aspect of its surroundings. This bold hypothesis, referred to as Newton’s First Law of Motion, is summarized by the idea that an object will maintain its state of motion, whether at rest or traveling at high speed, unless acted upon by some aspect of its surroundings.
Using the kinematic terminology developed in the last unit, this means that an object’s velocity (state of motion) is constant unless it interacts with some outside agent. An external interaction is not necessary for an object to move, it is only necessary if the object’s velocity changes. Thus, what is caused is not velocity, but acceleration. This concept is one of the most subtle, and complex, in all of physics.
Newton's Second Law
Newton also hypothesized that the sum total of all interactions with the external environment, which he termed forces, is directly proportional to the acceleration of the object. Moreover, the proportionality constant between the sum of all forces acting on an object and the acceleration of the object measures the “resistance” of an object to changes in its motion. This resistance to changes in motion is termed the inertia.
For example, an object with great inertia (quantified by a large proportionality constant) responds to the application of forces with a relatively small acceleration. An object with little inertia (a small proportionality constant) responds to the application of the same forces with a relatively large acceleration. The amount of inertia an object has is measured by the inertial mass of the object.
In summary, this relationship, known as Newton’s Second Law of Motion, and can be written mathematically as:
\Sigma F=m a \nonumber
where
- F is a force acting on the object from its surroundings, measured in Newtons (N),
- \Sigma (sigma) is a shorthand reminder to sum all of the forces acting on the object,
- and m is the mass of the object, measured in kilograms (kg).
The sum of all of the forces acting on an object will be referred to as the total force acting on the object.
Newton's Third Law
Newton’s third great contribution to the study of dynamics was his vision of force, defined to be the interaction between an object and some aspect of its surroundings. Newton theorized that since objects interact with other objects in their surroundings, always in pairs, a certain symmetry exists in nature. The distinction between the actor and the acted-upon is arbitrary. It would be just as easy to switch focus and consider the object in the surroundings as the actedupon and the original object of interest the actor.
If nature exhibits this symmetry, then the force that one object exerts on another must always be equal in magnitude to the force that the second object exerts on the first. To speak of one object as exerting a force on another is to speak of only one-half of the picture. This idea, known as Newton’s Third Law of Motion, is of central importance in the study of forces. In summary, objects interact with each other, and equal magnitude forces are exerted on each of the two objects interacting. A simplistic way of picturing this is the idea that you cannot touch something without being touched, and moreover that the harder you touch the harder you will be touched in return.
Investigating the dynamics of a situation involves the identification of all interactions an object experiences with other objects in its surroundings. To help in the identification of these interactions, and to use this information to better describe the ultimate motion of the object, a number of useful analysis tools are detailed below.
Analysis Tools
Drawing Free-Body Diagrams
The free-body diagram is by far the most important analysis tool for determining the interactions between an object and its surroundings. There are three distinct steps to creating a free-body diagram. Let’s walk through the steps for the situation described below:
A child pulls herself up a rope using only her hands.
1. Select the object you would like to study.
In this example, it is probably safe to assume that the object we would like to study is the child. However, depending on what we are investigating it may be the rope or even the ceiling we are interested in. Selecting the correct object to represent by a free-body diagram is a crucial step, especially in more complicated situations. With practice you will develop a knack for selecting the correct object to represent.
2. Draw a picture of the object of interest free from all other objects.
Notice that the rope does not appear in the diagram. As the name free-body implies, the object is drawn free of all external constraints.
3. Indicate on the diagram all interactions of the object with its environment.
Now comes the most difficult part of constructing a free-body diagram. It is crucial not to miss an interaction. If an interaction is overlooked, than the total of the forces will be incorrect, and the acceleration will be incorrect, and your entire analysis will be incorrect.
Also, only the portion of the interaction that acts on the girl should be indicated on a freebody diagram of the girl. For example, she is interacting with the rope. The rope’s action on the girl will be indicated, not the action of the girl on the rope.
To aid in the search for interactions, we will divide the types of interactions that the girl can be part of into two types, non-contact and contact.
- Non-Contact Interactions
Non-contact interactions include all interactions that can occur between the girl and objects in her surroundings that do not require direct physical contact between the two objects. Non-contact interactions include the interaction of the girl with the gravitational and electromagnetic fields in her vicinity. (How these fields are created and how they can affect the girl will slowly be incorporated into our physics model.)
At the current level of complexity, however, the only non-contact interaction you need worry about is the interaction of the girl with the gravitational field created by the earth, which we will simply term the force of gravity. The direction of this force is down, toward the center of the earth. - Contact Interactions
Contact interactions occur at every point on the girls’ body in which she is in direct physical contact with an external object. The most obvious of these is the rope. The girl is in contact with the rope, so the rope and girl exert forces on each other. These forces are equal in magnitude. Remember, however, that it is only the force exerted on the girl that is indicated on a free-body diagram of the girl. The location of this force is at the girls’ hands, and the direction of this force is up. (The direction of this force cannot be down, because that would imply that the rope is pushing the girl, as opposed to pulling her. It is impossible for a rope to push someone, unless it is a very stiff rope. Very stiff ropes will be called rods.)
The only other objects to actually make contact with the girl are air molecules. The air molecules interact with the girl on all sides, each exerting a small force directly inward, perpendicular to the girl’s body. Although each of these forces is very small, their sum is not always small. For example, if the girl were falling freely from an airplane the vast numbers of air molecules colliding with the girl from underneath, versus the rather small number colliding from above, and the strength of these collisions, would add to a very large force acting upward on the girl. This force could easily be equal in magnitude to the force of gravity on the girl. The force of air molecules on an object, referred to as air resistance, is often ignored in analyzing scenarios simply because of the difficulty of dealing with the complexity.
However, in many cases the effects of the air molecules are negligible compared to the other forces acting on the object. This is the case with the girl climbing the rope. The forces exerted by the air molecules are probably very close to being uniformly distributed around the girl’s surface. Thus, for every air molecule pushing her to the right, there is probably an air molecule pushing her to the left. These forces will add to a total force very close to zero.
A correct free-body diagram for the girl is shown below:
Since a coordinate system is crucial for translating motion diagrams and free-body diagrams into mathematical relationships, a coordinate system has been added to the free-body diagram. It is always a good idea to use the same coordinate system for both the free-body diagram and the motion diagram.
Calculating the Force of Gravity near the Surface of the Earth
In addition to creating the three laws of motion mentioned earlier, Newton also postulated the Law of Universal Gravitation. This law states that every object of mass in the universe creates a gravitational field, and every object of mass in the universe senses and interacts with every other objects’ field. That’s an awful lot of forces! To try to identify and estimate the magnitude of all of these forces on an object near the surface of the earth would be a lifelong task.
Luckily, the strength of the gravitational field depends on the mass of the object producing the field, and inversely as the square of the distance from the object. The more massive the object, the stronger the field. The closer the object, the stronger the field. Thus, since the earth is much more massive than any other nearby object, when creating free-body diagrams for objects near the surface of the earth we can safely include just the gravitational field due to the earth, ignoring all the other, relatively small, gravitational fields.
The magnitude of the gravitational field of a massive object (g) depends on the mass of the object (M), the distance from the center of the object (d), and a constant called, appropriately, the gravitational constant (G). The relationship is:
g=\frac{G M}{d^{2}} \nonumber
Near the surface of the earth, the gravitational field has a magnitude of approximately 9.8 N/kg. Although the gravitational field strength varies with the distance from the surface of the earth, we will ignore this slight variation unless explicitly told to include its effects.
The gravitational force felt by a massive object in the presence of a gravitational field is given by the product of the object’s mass and the magnitude of the gravitational field at the location of the object:
F_{\text {gravity }}=m g \nonumber
Applying Newton’s Second Law
Let’s return to the scenario under investigation and make some quantitative information more explicit. Then, we can attempt to further investigate the situation using Newton’s Second Law.
A 30 kg child pulls herself up a rope at approximately constant speed using only her hands.
Newton’s Second Law states:
\Sigma F=m a \nonumber
\Sigma F refers to the sum of all of the forces acting on the girl, the force of the rope (which is positive in our coordinate system) and the force of gravity (which is negative in our coordinate system). Thus,
F_{\text {rope }}-F_{\text {gravity }}=m a \nonumber
Since m = 30 kg, and a = 0 m/s2 (since she climbs at constant speed), the equation becomes:
F_{\text {rope }}-F_{\text {gravity }}=0 \nonumber
By Newton’s relationship for the force of gravity:
\begin{aligned} F_{\text {gravity }} &=m g \\ F_{\text {gravity }} &=(30 k g)\left(9.8 \frac{N}{k g}\right) \\ F_{\text {gravity }} &=294 N \end{aligned} \nonumber
Therefore:
\begin{array}{l} F_{\text {rope }}-294 N=0 \\ F_{\text {rope }}=294 N \end{array} \nonumber
Thus, Newton’s Second Law allows us to determine the force with which the rope pulls on the girl. Of course, by Newton’s Third Law, the force with which the girl pulls on the rope is equal in magnitude, so the girl exerts a 294 N force on the rope.
If the girl had not climbed the rope at approximately constant speed her acceleration would have to be determined, either from an explicit mention in the description or through using the kinematic relations developed in the last unit, and then inserted into Newton’s Second Law. If her acceleration had been directed upwards (positive) the force of the rope on the girl would have had to be larger. If her acceleration had been directed downwards (negative) the force of the rope on the girl would have had to be smaller.
Analyzing a More Complex Scenario
Before you start analyzing dynamics scenarios on your own, let's work our way through a more complex scenario.
To practice falling, a 55 kg pole-vaulter falls from rest off of a wall 5.0 m above a foam cushion. The pole-vaulter sinks about 1.8 m into the cushion before stopping.
Before we begin analyzing the forces acting on this pole-vaulter, I think we should try to get a handle on the kinematics of the situation. Therefore, our first step in analyzing this situation is to draw a motion diagram and tabulate motion information.
| Event 1: The instant she leaves the wall. | Event 2: The instant she hits the cushion. | Event 3: The instant she comes to rest. |
|---|---|---|
| t1 = 0 s | t2 = | t3 = |
| r1 = 0 m | r2 = 5.0 m | r3 = 6.8 m |
| v1 = 0 m/s | v2 = | v3 = 0 m/s |
| a12 = | a23 = |
Notice that between the instant she leaves the wall and the instant she hits the cushion the acceleration is positive (down), while between the instant she hits the cushion and the instant she comes to rest the acceleration is negative (up). Thus, when applying the kinematic relationships and Newton's Second Law we will have to be careful not to confuse variables between these two intervals.
What should jump out at you is the fact that this kinematic scenario cannot be solved! There are five unknown kinematic quantities and only four kinematic equations. Something else is needed in order to complete the kinematic description. Let's look at the forces acting on the pole-vaulter to see if we can figure out another piece of kinematic information.
Between the first two instants, the only force acting on the pole-vaulter is the force of gravity. Once she hits the cushion, however, there are two forces acting on the pole-vaulter, the force of gravity and the force of the cushion. Correct free-body diagrams for these two distinct phases of her motion are given below.
The diagram on the left corresponds to the first time interval and the diagram on the right to the second time interval. For each of these free-body diagrams, I will apply Newton's Second Law:
\begin{array}{ll} \Sigma F=m a_{12} & \qquad \qquad \qquad \Sigma F=m a_{23} \\ +F_{\text {gravity }}=(55 \mathrm{~kg}) a_{12} & \qquad \qquad \qquad +F_{\text {gravity }}-F_{\text {cushion }}=(55 \mathrm{~kg}) a_{23} \end{array} \nonumber
Since
\begin{aligned} F_{\text {gravity }} &=m g \\ F_{\text {gravity }} &=(55 \mathrm{~kg})\left(9.8 \frac{\mathrm{N}}{\mathrm{kg}}\right) \\ F_{\text {gravity }} &=539 \mathrm{~N} \end{aligned} \nonumber
\begin{array}{ll} 539 N=(55 \mathrm{~kg}) a_{12} & \qquad \qquad \qquad 539 N-F_{\text {cushion }}=(55 \mathrm{~kg}) a_{23} \\ a_{12}=9.8 \mathrm{~m} / \mathrm{s}^{2} & \end{array} \nonumber
Thus, from Newton's Second Law, we know that the acceleration during the fall is 9.8 m/s2. (We still don't know what the acceleration was during the impact portion of the motion.) Substituting this value back into the motion table yields:
| Event 1: The instant she leaves the wall. | Event 2: The instant she hits the cushion. | Event 3: The instant she comes to rest. |
|---|---|---|
| t1 = 0 s | t2 = | t3 = |
| r1 = 0 m | r2 = +5.0 m | r3 = +6.8 m |
| v1 = 0 m/s | v2 = | v3 = 0 m/s |
| a12 = 9.8 m/s2 | a23 = |
This is now solvable, using strictly kinematics, for the four remaining unknowns. Try to do the math on your own, and compare your result to:
| Event 1: The instant she leaves the wall. | Event 2: The instant she hits the cushion. | Event 3: The instant she comes to rest. |
|---|---|---|
| t1 = 0 s | t2 = 1.0 s | t3 = 1.36 s |
| r1 = 0 m | r2 = +5.0 m | r3 = +6.8 m |
| v1 = 0 m/s | v2 = +9.9 m/s | v3 = 0 m/s |
| a12 = 9.8 m/s2 | a23 = -27 m/s2 |
We now have a complete kinematic description of the motion.
Returning to Newton's Second Law for the impact portion of the motion,
\begin{array}{l} 539 N-F_{\text {cushion }}=(55 \mathrm{~kg}) a_{23} \\ 539 N-F_{\text {cushion }}=(55 \mathrm{~kg})\left(-27 \mathrm{~m} / \mathrm{s}^{2}\right) \\ 539 N-F_{\text {cushion }}=-1485 \mathrm{~N} \\ F_{\text {cushion }}=2024 \mathrm{~N} \end{array} \nonumber
The cushion exerts a force of about 2000 N on the pole-vaulter to stop her fall.
Hints and Suggestions
The Magnitude of the Gravitational Field
Quite often, students make a pair of mistakes when dealing with the magnitude of the gravitational field, g.
1. ‘g’ is never negative.
Since g is the magnitude of the gravitational field, it cannot be a negative number. As a magnitude, it does not have a direction associated with it! Resist all temptation to replace ‘g’ with the value “-9.8 N/kg”!
Part of the confusion lies with the fact that the gravitational field does have an associated direction. The gravitational field of the earth is directed downward toward the center of the earth. Even so, the gravitational field is not negative. Negative only makes sense relative to a coordinate system, and since you are always free to choose any system you want, the gravitational field is just as likely to be oriented in the positive as the negative direction
2. ‘g’ is not an acceleration.
Often, students have learned that ‘g’ is the “acceleration due to gravity.” However, as I sit here in a chair writing this book, the force of gravity is acting on me and I am most definitely not accelerating at 9.8 m/s2! In fact, the force of gravity has acted on me for every second of my life and only very rarely have I accelerated at 9.8 m/s2. ‘g’ measures the strength of the gravitational field. As such, it is related to the gravitational force, which, like all forces, can give raise to accelerations. However, it is the total force acting on an object that determines its acceleration, not simply the force of gravity.
It is true that the units of ‘g’, N/kg, are also the units of acceleration, since a Newton is defined to be a kg m/s2. It is also true that in a very specific scenario2, when the only force acting on an object is the force of gravity, the magnitude of the object’s acceleration is numerically equal to ‘g’. However, there are also very specific scenarios in which the acceleration of an object is numerically equal to 4.576 m/s2, or 62.31452 m/s2. The strength of physics is its ability to analyze diverse scenarios with the same small set of tools, not to develop specialized tools tailored to every different specific scenario. Newton’s Second Law will always allow you to determine an object’s acceleration, whether the force of gravity acts alone or not.
Note
2 When the only force acting on an object is the force of gravity, the situation is termed freefall.
Newton’s Third Law
Many physics students have heard the saying, “For every action there is an equal and opposite re-action.” I was forced to memorize this statement in a middle-school science class, and was told it was called Newton’s Third Law. I’m sure I had no idea what it really meant. It states that there is a reaction to every action, which seems to imply the “action” happens first. This isn’t what the law means. There really is no separation or possible distinction between action and reaction. A better way to look at it is that there is an interaction between two objects, and the two “sides” of this interaction experience exactly the same force. Of course, the effect of this mutually symmetrical force acting on the two objects need not be identical.
As a test of your understanding of Newton’s Third Law, try to answer the following question:
Note
As you drive along the highway, a mosquito splats against your car windshield. During the collision between the mosquito and the car,
a. the force on the mosquito was greater in magnitude than the force on the car.
b. the force on the car was greater in magnitude than the force on the mosquito.
c. the force on the mosquito was equal in magnitude to the force on the car.
d. it is impossible to determine the relative sizes of the forces without more information.
As strange as it may seem, the correct answer is ‘c’. The forces exerted on the mosquito and the car are equal in magnitude. In the terminology used in this chapter, the mosquito and car interact (probably an unpleasant interaction for the mosquito), and in an interaction the two agents involved exert equal forces on each other.
However, obviously something is different about the interaction from the mosquito’s perspective. What is different is not the force acting on the mosquito but rather its acceleration. Although the forces acting on the mosquito and car are the same, the mosquito’s acceleration is much greater than the car’s acceleration because the mosquito’s mass is much smaller than the car’s mass. The acceleration of the car is so small that it is not even noticed by the driver, while the acceleration of the mosquito is certainly noticed by the mosquito!
Activities
Construct free-body diagrams for the objects described below.
a. When throwing a ball vertically upward, my hand moves through a distance of about 1.0 m before the ball leaves my hand. The 0.80 kg ball reaches a maximum height of about 20 m above my hand.
while the ball is in my hand
after the ball leaves my hand
b. To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a 2.0 m thick foam cushion resting on the ground. However, he misses the cushion.
while falling through the air
while being stopped by the ground
c. A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light.
the top light
the bottom light
Construct free-body diagrams for the objects described below.
a. A 4000 kg rocket’s engine produces a thrust of 70,000 N for 15 s. The rocket is fired vertically upward.
while the engine is firing
after the engine turns off
b. Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. An 84 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the 84 kg block is released, the student is pulled up to his dorm room.
the student
the block
c. A 1.0 kg block is stacked on top of a 2.0 kg block on the floor of an elevator moving downward at constant speed.
the 1.0 kg block
the 2.0 kg block
A block hangs from the ceiling of an elevator by a string. For each of the following situations, circle the correct relationship symbol between the magnitude of the force of the string on the block and the magnitude of the force of gravity on the block and explain your reasoning.
a. The elevator is at rest.
\mathrm{F}_{\text {string on block }}> \boxed{=} < \ ? \quad \mathrm{F}_\text{gravity on block }\nonumber
Explanation:
Since the block is not accelerating, the two forces acting on it must be equal in magnitude.
b. The elevator is moving upward at an constant speed.
F_{\text {string on block }}>\boxed{=}< \ ? \quad F_\text{gravity on block } \nonumber
Explanation:
Since the block is still not accelerating, the two forces acting on it must be equal in magnitude.
c. The elevator is moving downward at a decreasing speed.
F_\text{string on block } \boxed{>} \ =\ <\ ? \quad F_\text {gravity on block } \nonumber
Explanation:
Since the block is accelerating upward, the force directed upward (the force of the string) must be larger than the force directed downward (the force of gravity).
d. The elevator is moving upward at an increasing speed.
F_\text{string on block } \boxed{>} \ =\ <\ ? \quad F_\text {gravity on block } \nonumber
Explanation:
The block is accelerating upward, so the force directed upward must be larger than the force directed downward
A man stands on a bathroom scale inside of an elevator. For each of the following situations, circle the correct relationship symbol between the magnitude of the force of the scale on the man and the magnitude of the force of gravity on the man and explain your reasoning.
a. The elevator is at rest.
F_\text {scale on man } \quad >\ =\ <\ ? \quad F_\text {gravity on man } \nonumber
Explanation:
b. The elevator is moving downward at a constant speed.
F_\text {scale on man } \quad >\ =\ <\ ? \quad F_\text {gravity on man } \nonumber
Explanation:
c. The elevator is moving downward at a increasing speed.
F_\text {scale on man } \quad >\ =\ <\ ? \quad F_\text {gravity on man } \nonumber
Explanation:
d. The elevator is moving upward at a decreasing speed.
F_\text {scale on man } \quad >\ =\ <\ ? \quad F_\text {gravity on man } \nonumber
Explanation:
Two blocks are stacked on top of each other on the floor of an elevator. For each of the following situations, circle the correct relationship symbol between the two force magnitudes and explain your reasoning.
a. The elevator is moving downward at a constant speed.
F_\text {bottom block on top block} \quad >\ =\ <\ ? \quad F_\text {top block on bottom block}\nonumber
Explanation:
F_\text {bottom block on top block} \quad >\ =\ <\ ? \quad F_\text {gravity on top block}\nonumber
Explanation:
b. The elevator is moving downward at an increasing speed.
F_\text {bottom block on top block} \quad >\ =\ <\ ? \quad F_\text {top block on bottom block}\nonumber
Explanation:
F_\text {bottom block on top block} \quad >\ =\ <\ ? \quad F_\text {gravity on top block}\nonumber
Explanation:
c. The elevator is moving upward at a decreasing speed.
F_\text {bottom block on top block} \quad >\ =\ <\ ? \quad F_\text {top block on bottom block}\nonumber
Explanation:
F_\text {bottom block on top block} \quad >\ =\ <\ ? \quad F_\text {gravity on top block}\nonumber
Explanation:
a. If the graph is of position vs. time, rank these graphs on the basis of the total force acting on the object.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. If the graph is of velocity vs. time, rank these graphs on the basis of the total force acting on the object.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are six automobiles traveling at constant velocity. The automobiles have different masses and velocities. Rank these automobiles on the basis of the magnitude of the total force acting on them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are six identical baseballs shortly after being thrown. At the instant shown, the baseball’s velocity is indicated, along with the distance the ball has traveled and the elapsed time since leaving the thrower’s hand. Rank these baseballs on the basis of the magnitude of the force of the thrower’s hand currently acting on them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are three blocks stacked on top of each other at rest. Rank the magnitude of the forces referred to below from largest to smallest.
A The force of the 3 kg block on the 2 kg block
B The force of the 2 kg block on the 3 kg block
C The force of the 3 kg block on the 1 kg block
D The force of the 1 kg block on the 3 kg block
E The force of the 2 kg block on the 1 kg block
F The force of the 1 kg block on the 2 kg block
G The force of the 1 kg block on the floor
H The force of the floor on the 1 kg block
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are three blocks stacked on top of each other inside of an elevator moving upward at increasing speed. Rank the magnitude of the forces referred to below from largest to smallest.
A The force of the 3 kg block on the 2 kg block
B The force of the 2 kg block on the 3 kg block
C The force of the 3 kg block on the 1 kg block
D The force of the 1 kg block on the 3 kg block
E The force of the 2 kg block on the 1 kg block
F The force of the 1 kg block on the 2 kg block
G The force of the 1 kg block on the floor of the elevator
H The force of the floor of the elevator on the 1 kg block
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
For each of the collisions illustrated below, circle the correct relationship symbol between the magnitude of the force of car A on car B and the magnitude of the force of car B on car A and explain your reasoning.
a.
\begin{array}{l} F_{\text {car } A \text { on car B}} \quad>\ =\ <\ ? \quad F_{\text {car B on car A }} \end{array} \nonumber
Explanation:
b.
\begin{array}{l} F_{\text {car } A \text { on car B}} \quad>\ =\ <\ ? \quad F_{\text {car B on car A }} \end{array} \nonumber
Explanation:
c.
\begin{array}{l} F_{\text {car } A \text { on car B}} \quad>\ =\ <\ ? \quad F_{\text {car B on car A }} \end{array} \nonumber
Explanation:
A 100 kg man concerned about his weight decides to weigh himself in an elevator. He stands on a bathroom scale in an elevator that is moving upward at 3.0 m/s. As the elevator reaches his floor, it slows to a stop over a distance of 2.0 m.
Motion Diagram
Motion Information
| Event 1: The instant the elevator begins to slow. | Event 2: The instant it stops. |
|---|---|
| t1 = 0 s | t2 = |
| r1 = 0 m | r2 = + 2.0 m |
| v1 = 3.0 m/s | v2 = 0 m/s |
| a12 = | |
Free-Body Diagram
Mathematical Analysis
Since there are only two unknown kinematic quantities, we can determine them by our two kinematic equations.
\begin{array}{l} v_{2}=v_{1}+a_{12}\left(t_{2}-t_{1}\right) \\ \left.0=3+a_{12} t_{2}-0\right) \\ a_{12}=\frac{-3}{t_{2}} \end{array}\nonumber
Now substitute this expression into the other equation:
\begin{array}{l} r_{2}=r_{1}+v_{1}\left(t_{2}-t_{1}\right)+\frac{1}{2} a_{12}\left(t_{2}-t_{1}\right)^{2} \\ 2=3 t_{2}+\frac{1}{2} a_{12} t_{2}^{2} \\ 2=3 t_{2}+\frac{1}{2}\left(\frac{-3}{t_{2}}\right) t_{2}^{2} \\ 2=3 t_{2}-1.5 t_{2} \\ 2=1.5 t_{2} \\ t_{2}=1.33 s \end{array}\nonumber
Substitute this result back into the original equation:
\begin{array}{l} a_{12}=\frac{-3}{1.33} \\ a_{12}=-2.25 \mathrm{~m} / \mathrm{s}^{2} \end{array}\nonumber
Now apply Newton’s Second Law to the man:
\begin{array}{l} \Sigma F=m a \\ F_{\text {scale }}-F_{\text {gravity }}=(100)(-2.25) \\ F_{\text {scale }}-(100)(9.8)=-225 \\ F_{\text {scale }}=755 N \end{array} \nonumber
A 40 kg child is hanging from a rope by her hands. She exerts a burst of strength and 2.0 s later is traveling at 1.4 m/s up the rope.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| t1 = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis14
A 55 kg pole-vaulter, just before touching the cushion on which she lands after a jump, is falling downward at a speed of 10 m/s. The pole-vaulter sinks about 2.0 m into the cushion before stopping.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| t1 = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis15
A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light. The elevator is moving downward at 4.0 m/s when someone presses the emergency stop button. The elevator comes to rest in 1.2 seconds.
Motion Diagram
Motion Information
| Event 1: The stop button is pressed | Event 2: The elevator stops. |
|---|---|
| t1 = 0 s | t2 = 1.2 s |
| r1 = 0 m | r2 = |
| v1 = 4.0 m/s | v2 = 0 m/s |
| a12 = | |
Free-Body Diagram
Mathematical Analysis
Since there are only two unknown kinematic quantities, we can determine them by our two kinematic equations. Note that both lights have the same kinematic description.
\begin{array}{l} 0=4+a_{12}(1.2-0) \\ a_{12}=-3.33 \mathrm{~m} / \mathrm{s}^{2} \end{array} \nonumber
\begin{array}{l} r_{2}=0+4(1.2-0)+\frac{1}{2}(-3.33)(1.2-0)^{2} \\ r_{2}=2.4 m \end{array} \nonumber
Now apply Newton’s Second Law to the two lights:
bottom light
\begin{array}{l} -F_{\text {bottomcable }}+F_{\text {gravity }}=m a \\ -F_{\text {bottomcable }}+(0.8)(9.8)=(0.8)(-3.33) \\ F_{\text {bottomcable }}=10.5 N \end{array} \nonumber
top light
\begin{array}{l} -F_{\text {topcable }}+F_\text {bottomcable}+F_{\text {gravity }}=m a \\ -F_{\text {topcable }}+10.5+(2.0)(9.8)=(2.0)(-3.33) \\ F_{\text {topcable }}=36.8 N \end{array} \nonumber
A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light. The elevator is moving downward at 4.0 m/s when someone presses the emergency stop button. During the stop, the upper cable snaps. The elevator engineer says that the cable could withstand a force of 40 N without breaking.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| t1 = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis16
A 70 kg student is 120 m above the ground, moving upward at 3.5 m/s, while hanging from a rope hanging from a 280 kg helium balloon. The lift on the balloon due to the buoyant force is 3000 N.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| t1 = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis17
To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a foam cushion. The pole-vaulter sinks about 1.4 m into the cushion before stopping.
Motion Diagram
Motion Information
| Event 1: | Event 2: | Event 3: |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis18
To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a 2.0 m thick foam cushion resting on the ground. However, he misses the cushion. The pole-vaulter sinks about 0.10 m into the ground before stopping.
Motion Diagram
Motion Information
| Event 1: | Event 2: | Event 3: |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis19
When throwing a 0.80 kg ball vertically upward, my hand moves through a distance of about 1.0 m before the ball leaves my hand. The ball leaves my hand at 35 m/s.
Motion Diagram
Motion Information
| Event 1: | Event 2: | Event 3: Ball reaches its max height |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis20
A 4000 kg rocket’s engine produces a thrust of 70,000 N for 15 s. The rocket is fired vertically upward.
Motion Diagram
Motion Information
| Event 1: | Event 2: | Event 3: Rocket reaches its max height |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis21
Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. An 84 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the 84 kg block is released, the student is pulled up to his dorm room, 8.0 m off the ground.
Motion Diagram
Motion Information
| Object: Student | |
|---|---|
| Event 1: Block is released | Event 2: Student reaches room. |
| t1 = = 0 s | t2 = |
| r1 = 0 m | r2 = +8.0 m |
| v1 = 0 m/s | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis
Since there are three kinematic variables, we will have to analyze the forces first:
student
\begin{array}{l} F_{\text {rope }}-F_{\text {gravity }}=m a \\ F_{\text {rope }}-(80)(9.8)=80 a_{\text {student }} \end{array} \nonumber
block
\begin{array}{l} F_{\text {rope }}-F_{\text {gravity }}=m a \\ F_{\text {rope }}-(84)(9.8)=84 a_{\text {block }} \end{array}\nonumber
Because they are tied together, the acceleration of the student and the acceleration of the block are equal in magnitude, but opposite in direction. Therefore, a_{\text {block }}=-a_{\text {student. }}
\begin{array}{l} F_{\text {rope }}-784=80 a_{\text {student }} \\ F_{\text {rope }}=80 a_{\text {student }}+784 \end{array} \nonumber
\begin{array}{l} F_{\text {rope }}-823=84\left(-a_{\text {student }}\right) \\ \left(80 a_{\text {student }}+784\right)-823=-84 a_{\text {student }} \\ 164 a_{\text {student }}=39 \\ a_{\text {student }}=0.24 \mathrm{~m} / \mathrm{s}^{2} \end{array} \nonumber
We can now complete the kinematic description of the student’s motion:
\begin{array}{l} 8=0+0\left(t_{2}-0\right)+\frac{1}{2}(0.24)\left(t_{2}-0\right)^{2} \\ t_{2}=8.18 s \end{array} \nonumber
\begin{array}{l} v_{2}=0+0.24(8.18-0) \\ v_{2}=1.96 \mathrm{~m} / \mathrm{s} \end{array} \nonumber
Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. A block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room, 8 m off the ground, in a time of 1.8 s.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis22
Tired of walking down the stairs, an 80 kg engineering student designs an ingenious device for reaching the ground from his third floor dorm room. A block, at rest on the ground, is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the student steps out of the window, she falls the 8 m to the ground in a time of 1.8 s.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis23
A 60 kg student lifts herself from rest to a speed of 1.5 m/s in 2.1 s. The chair has a mass of 35 kg.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis24
A 60 kg student lowers herself down 40 m at a constant speed of 1.0 m/s. The chair has a mass of 35 kg.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis25
A man of mass m, concerned about his weight, decides to weigh himself in an elevator. He stands on a bathroom scale in an elevator moving upward at speed v. As the elevator reaches his floor, it slows to a stop over a distance, d. Determine the reading on the bathroom scale (Fscale) as a function of m, v, d, and g.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis
Questions
If v = 0 m/s, what should Fscale equal? Does your function agree with this observation?
If d = ∞, what should Fscale equal? Does your function agree with this observation?
For what stopping distance, d, would the bathroom scale read 0 N? Would the scale also read 0 N for this stopping distance if the elevator was initially moving downward?
A falling pole-vaulter of mass m lands on a cushion at speed v. The pole-vaulter sinks a distance d into the cushion before stopping. Determine the force exerted on the pole-vaulter due to the cushion (Fcushion) as a function of m, v, d, and g.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis
Questions
If v = 0 m/s, what should Fcushion equal? Does your function agree with this observation?
If d = 0 m, what should Fcushion equal? Does your function agree with this observation?
What would be worse for the pole-vaulter, hitting the cushion at twice her original speed or sinking half of the original distance into the cushion?
A pole-vaulter of mass m falls off a wall a distance D above a cushion. The pole-vaulter sinks a distance d into the cushion before stopping. Determine the force exerted on the pole-vaulter due to the cushion (Fcushion) as a function of m, D, d, and g.
Motion Diagram
Motion Information
| Event 1: | Event 2: | Event 3: |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis
Questions
If D = ∞, what should Fcushion equal? Does your function agree with this observation?
If d = 0 m, what should Fcushion equal? Does your function agree with this observation?
What would be worse for the pole-vaulter, starting at twice the initial distance above the cushion or sinking half of the original distance into the cushion?
Tired of walking up the stairs, an engineering student of mass m designs an ingenious device for reaching his third floor dorm room. A block of mass M is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room in a time T. Determine the velocity of the student (v) when he reaches his room as a function of m, M, T and g.
Motion Diagram
Motion Information
| Object: | |
|---|---|
| Event 1: | Event 2: |
| t1 = = | t2 = |
| r1 = | r2 = |
| v1 = | v2 = |
| a12 = | |
Free-Body Diagram
Mathematical Analysis
Questions
If g = 0 m/s2, what should v equal? Does your function agree with this observation?
If m = M, what should v equal? Does your function agree with this observation?
If M = ∞, what should v equal? Does your function agree with this observation?
A rocket of mass m is fired vertically upward from rest. The rocket’s engine produces a thrust of constant magnitude Fthrust for tthrust seconds. Determine the maximum height reached by the rocket (H) as a function of Fthrust, tthrust, m, and g.
Motion Information
| Event 1: | Event 2: | Event 3: |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis
Questions
If g = 0 m/s2, what should H equal? Does your function agree with this observation?
If Fthrust = mg, what should H equal? Does your function agree with this observation?
A rocket of mass m is fired vertically upward from rest. The rocket’s engine produces a thrust of constant magnitude Fthrust for tthrust seconds. Determine the time it takes the rocket to reach its apex (tapex) as a function of Fthrust, tthrust, m, and g.
Motion Information
| Event 1: | Event 2: | Event 3: |
|---|---|---|
| t1 = | t2 = | t3 = |
| r1 = | r2 = | r3 = |
| v1 = | v2 = | v3 = |
| a12 = | a23 = |
Free-Body Diagram
Mathematical Analysis
Questions
If g = 0 m/s2, what should tapex equal? Does your function agree with this observation?
If Fthrust = mg, what should tapex equal? Does your function agree with this observation?
Conservation Laws
Concepts and Principles
What is a Conservation Law?
In general, a conservation law is a statement that a certain quantity does not change over time. If you know how much of this quantity you have today, you can be assured that the exact same amount of the quantity will be available tomorrow. A famous (at least to physicists) explanation of the nature of a conservation law was given by Richard Feynman.
Imagine your child has a set of 20 wooden blocks. Every day before bedtime you gather up your child's blocks to put them away. As you gather up the blocks, you keep count in your head. Once you reach 20, you know you have found all of the blocks and it is unnecessary for you to search any longer. This is because the number of blocks is conserved. It is the same today as it was yesterday.
If one day you only find 18 blocks, you know to keep looking until you find the missing 2 blocks. Also, with experience, you discover the typical hiding places for the blocks. You know to check under the sofa, or behind the curtains.
If your child is rambunctious, you may even have to look outside of the room. Perhaps he threw a block or two out of the window. Even though blocks can disappear from inside of the room, and appear out in the yard, if you search everywhere you will always find the 20 blocks.
Physicists have discovered a number of quantities that behave exactly like the number of wooden blocks. We will examine two of these quantities, energy and momentum, below.
The Impulse-Momentum Relation
While Newton’s Second Law directly relates the total force that acts on an object at a specific time to the object’s acceleration at that exact same time, conservation laws relate the amount of a certain quantity present at one time to the amount present at a later time.
The first conserved quantity we will investigate is momentum. Of course, just because momentum is conserved doesn't mean that the momentum of any particular object or system of objects is always constant. The momentum of a single object, like the number of blocks in the playroom, can change. Just as blocks can be thrown out of the window of the playroom, the momentum of a single object can be changed by applying impulse to it. The relationship between impulse and momentum is, conceptually,
\text { initial momentum }+\text { impulse }=\text { final momentum } \nonumber
Pictorially, we can visualize this as
In practice, we will identify an object or collection of objects (a system) and determine the amount of momentum the system contains at some initial time. This quantity cannot change unless impulse is done to the system. We call processes that bring momentum into the system as positive impulses, and processes that remove momentum from the system as negative impulses.
Mathematically this is written as
\begin{array}{l} \begin{gather*} \text { initial momentum }+\text { impulse }=\text { final momentum } \\ P_{i}+J_{i f}=P_{f} \\ \Sigma m v_{i}+\Sigma F(\Delta t)=\Sigma m v_{f} \end{gather*} \end{array} \nonumber
where
- momentum (P) is the product of an object’s mass and velocity,
- impulse (J) is the product of a force external to the system and the time interval over which it acts,
- and \Sigma indicates that you must sum the momentum of all of the objects in the system and all of the impulses acting on the system.
In short, if no impulse is applied to a system, its momentum will remain constant. However, if an impulse is applied to the system, its momentum will change by an amount exactly equal to the impulse applied. This momentum does not appear or disappear without a trace. It is simply transferred to the object supplying the impulse. In this sense, impulse is the transfer of momentum into or out of a system, analogous to tossing blocks into or out of a playroom.
The Work-Energy Relation
The second conserved quantity we will investigate is energy. Just like momentum, or wooden blocks, the conservation of energy doesn't mean that the energy of any particular object is always constant. The energy of a single object or system of objects can be changed by doing work to it. The relationship between work and energy is, conceptually,
\text { initial energy }+\text { work }=\text { final energy } \nonumber
Pictorially, we can visualize this as
The similarity between momentum and energy is not complete, however. While there is only one form of momentum (i.e., one hiding place for momentum “blocks”) there are several forms of energy. These different forms of energy will be introduced as you progress through more and more complicated models of the physical world. For now, the only “hiding place” I want to discuss is kinetic energy. In terms of kinetic energy, the above conceptual relationship between work and energy becomes, expressed mathematically,
\begin{array}{l} \begin{gather*} \text { initial energy }+\text { work }=\text { final energy } \\ \qquad K E_{i}+W_{i f}=K E_{f} \\ \Sigma \frac{1}{2} m v_{i}^{2}+\Sigma|F \| \Delta r| \cos \phi=\Sigma \frac{1}{2} m v_{f}^{2} \end{gather*} \end{array} \nonumber
where
- kinetic energy (KE) is the product of one-half an object’s mass and squared velocity,
- work (W) is the product of a force (even an internal force) and the displacement over which it acts (with more subtle details discussed below),
- \Sigma indicates that you must sum the kinetic energy of all of the objects in the system and all of the work done to the system,
- and we define a new unit, Joule (J), as J = kg (m/s)2 = N m
Unlike anything we’ve studied up to this point, the work-energy relation is a scalar equation. This will become especially important when we study objects moving in more than one dimension. For now, all this means is that in the expression for work, |F \| \Delta r| \cos \phi, we should use the magnitude of the force and the magnitude of the change in position. This product is then multiplied by \cos \phi, where \phi is defined to be the angle between the applied force and the displacement of the object. If the force and displacement are in the same direction \phi=0^{\circ}, and the work is positive (the object gains energy). If the force and displacement are in the opposite direction \phi=180^{\circ} , and the work is negative (the object loses energy). Note that the actual directions of the force and the displacement are unimportant, only their directions relative to each other affect the work.
In general, if no work is done to a system, its kinetic energy will remain constant. However, if work is done to system, its total energy will change by an amount exactly equal to the work done. Work is the transfer of energy from one system to another, again analogous to tossing blocks from the playroom into the yard.
Analysis Tools
Applying the Impulse-Momentum Relation to a Single Object
Let’s investigate the following scenario:
A 0.35 kg model rocket is fitted with an engine that produces a thrust of 11.8 N for 1.8 s. The rocket is launched vertically upward.
To apply the impulse-momentum relation, you must clearly specify the initial and final events at which you will tabulate the momentum. For example:
| Event 1: The instant the engine is ignited. | Event 2: The instant the rocket reaches maximum height. |
|---|---|
| P1 = 0 | P2 = (0.35) v2 |
| \mathrm{J}_{12}=+F_{\text {exhaust }}(1.8)-F_{\text {gravity }}(1.8) | |
Note that each external force acting on the rocket is multiplied by the time interval over which it acts. (Also note that the rocket’s engine does not produce a force on the rocket! The engine produces a downward force on the hot exhaust gases emitted from the engine and these hot gases exert an equal magnitude force back up on the rocket. That is why the force on the rocket is labeled as Fexhaust rather than Fengine.)
Applying impulse-momentum to the rocket during this time interval yields:
\begin{array}{l} P_{1}+J_{12}=P_{2} \\ 0+F_{\text {exhaust }}(1.8)-F_{\text {gravity }}(1.8)=0.35 v_{2} \\ 0+(11.8)(1.8)-(0.35)(9.8)(1.8)=0.35 v_{2} \\ v_{2}=43.0 \mathrm{~m} / \mathrm{s} \end{array} \nonumber
Thus, the rocket is traveling at 43.0 m/s at the instant the engine shuts off.
Of course, there is no reason why we had to analyze the rocket’s motion between the two instants of time we selected above. We could have selected the events:
| Event 1: The instant the engine is ignited. | Event 2: The instant the rocket reaches maximum height. |
|---|---|
| P1 = | P2 = 0 |
| \mathrm{J}_{12}=+F_{\text {exhaust }}(1.8)-F_{\text {gravity }}(\Delta t) | |
During this time interval, the force of the exhaust gases only act on the rocket for a portion of the entire time interval. Noting that the rocket’s velocity when it reaches its maximum height is zero, impulse-momentum would look like this:
\begin{array}{l} P_{1}+J_{12}=P_{2} \\ 0+F_{\text {exhaust }}(1.8)-F_{\text {gravity }}(\Delta t)=0 \\ 0+(11.8)(1.8)-(0.35)(9.8)(\Delta t)=0 \\ \Delta t=6.19 s \end{array} \nonumber
Thus, the rocket is in the air for 6.19 s before reaching its maximum height.
Applying the Work-Energy Relation to a Single Object
The work-energy relation also has many uses for investigating physical scenarios. For example, let’s look again at our model rocket:
A 0.35 kg model rocket is fitted with an engine that produces a thrust of 11.8 N for 1.8 s. The rocket is launched vertically upward.
Assuming we’ve already analyzed this scenario using impulse-momentum, what additional information can we extract using work-energy?
| Event 1: The instant the engine is ignited. | Event 2: The instant the engine shuts off. |
|---|---|
| KE1 = 0 | \mathrm{KE}_{2}=1 / 2 \ (0.35)(43)^{2} |
| \mathrm{W}_{12}=F_{\text {exhaust }}(\Delta r) \cos 0+F_{\text {gravity }}(\Delta r) \cos 180 | |
Therefore,
\begin{array}{l} K E_{1}+W_{12}=K E_{2} \\ 0+\left|F_{\text {exhaust }} \| \Delta r\right| \cos 0+\left|F_{\text {gravity }}\right||\Delta r| \cos 180=\frac{1}{2}(0.35)(43.2)^{2} \\ 0+11.8(\Delta r)(1)+(0.35)(9.8)(\Delta r)(-1)=327 \\ 11.8 \Delta r-3.43 \Delta r=327 \\ \Delta r=39.1 \mathrm{~m} \end{array} \nonumber
Thus, the rocket rises to a height of 39.1 m before the engines shuts off.
What if we apply work-energy between the following two events:
| Event 1: The instant the engine is ignited. | Event 2: The instant the rocket reaches its maximum height |
|---|---|
| KE1 = 0 | KE2 = 0 |
| \mathrm{W}_{12}=F_{\text {exhaust }}(39) \cos 0+F_{\text {gravity }}(\Delta r) \cos 180 | |
During this time interval, the force of the exhaust gases only act on the rocket for a portion of the entire displacement, namely 39 m, while the force of gravity acts over the entire displacement.
\begin{array}{l} K E_{1}+W_{12}=K E_{2} \\ 0+(11.8)(39) \cos 0+(0.35)(9.8)(\Delta r) \cos 180=0 \\ 0+460-3.43 \Delta r=0 \\ \Delta r=134 m \end{array} \nonumber
Thus, the maximum height reached by the rocket is 134 m.
Gravitational Potential Energy
In any situation in which an object changes its height above the surface of the earth, the force of gravity does work on the object. It is possible to calculate this work in general, and to rewrite the work-energy relation in such a way as to incorporate the effects of this work. This is referred to as constructing a potential energy function for the work done by gravity.
Let’s imagine an object of mass, m, located an initial height, hi, above the zero of a vertical coordinate system, with the upward direction designated positive. It moves to a final height of hf.
To calculate the work done by gravity on this object:
\begin{array}{l} W_{\text {gravity }}=|F \| \Delta r| \cos \phi \\ W_{\text {gravity }}=(m g)\left(h_{f}-h_{i}\right) \cos 180 \\ W_{\text {gravity }}=-m g h_{f}+m g h_{i} \end{array} \nonumber
The “mgh” terms are referred to as gravitational potential energy. Thus, the work done by gravity can be thought of as changing the gravitational potential energy of the object. Let’s plug the above result into the work-energy relation:
\begin{array}{l} \frac{1}{2} m v_{i}^{2}+\Sigma|F \| \Delta r| \cos \phi=\frac{1}{2} m v_{f}^{2} \\ \frac{1}{2} m v_{i}^{2}+\Sigma|F \| \Delta r| \cos \phi+W_{\text {gravity }}=\frac{1}{2} m v_{f}^{2} \\ \frac{1}{2} m v_{i}^{2}+\Sigma|F \| \Delta r| \cos \phi-m g h_{f}+m g h_{i}=\frac{1}{2} m v_{f}{ }^{2} \\ \frac{1}{2} m v_{i}^{2}+m g h_{i}+\Sigma|F \| \Delta r| \cos \phi=\frac{1}{2} m v_{f}^{2}+m g h_{f} \end{array} \nonumber
Therefore, this final relation:
\begin{array}{l} K E_{i}+G E_{i}+W_{i f}=K E_{f}+G E_{f} \\ \frac{1}{2} m v_{i}^{2}+m g h_{i}+\Sigma|F \| \Delta r| \cos \phi=\frac{1}{2} m v_{f}^{2}+m g h_{f} \end{array} \nonumber
can (and will) be used in place of the standard work-energy relation provided:
- You do not include the force of gravity a second time by calculating the work done by gravity. Basically, in this relationship gravity is no longer thought of as a force that does work on objects but rather as a source of potential energy.
- You calculate the initial and final heights, hi and hf, using a coordinate system in which the upward direction is positive.
Applying Work-Energy with Gravitational Potential Energy
Let’s use the work-energy relation, with gravitational potential energy terms, to re-analyze the previous scenario:
A 0.35 kg model rocket is fitted with an engine that produces a thrust of 11.8 N for 1.8 s. The rocket is launched vertically upward.
Let’s apply work-energy between the following two events, setting the initial elevation of the rocket equal to zero:
| Event 1: The instant the engine is ignited. | Event 2: The instant the rocket reaches its maximum height |
|---|---|
| KE1 = 0 | KE2 = 0 |
| GE1 = 0 | GE2 = (0.35)(9.8) h2 |
| \mathrm{W}_{12}=F_{\text {exhaust }}(39) \cos 0 | |
During this time interval, the force of the exhaust gases only act on the rocket for a portion of the entire displacement, namely 39 m. Remember, the force of gravity does not do work in this way of modeling nature, rather the gravitational energy of the rocket changes as it changes its elevation.
\begin{array}{l} K E_{i}+G E_{i}+W_{i f}=K E_{f}+G E_{f} \\ 0+0+(11.8)(39) \cos 0=0+(0.35)(9.8) h_{f} \\ 0+0+460=0+3.43 h_{f} \\ h_{f}=134 m \end{array} \nonumber
results in, of course, the same maximum height reached by the rocket.
Applying the Impulse-Momentum Relation to a Collision
Probably the most useful application of the impulse-momentum relation is in the study of collisions. For example:
Far from the earth, a 250 kg space probe, moving at 5 km/s, collides head-on with a 60 kg piece of space debris initially at rest. The debris becomes entangled in the probe’s solar collectors.
Let’s choose:
| Event 1: The instant before the collision. | Event 2: The instant the debris and probe reach a common velocity. |
|---|---|
| Object: Space Probe | |
| P1 = (250)(5000) | P2 = 250 v2 |
| \mathrm{J}_{12}=-F_{\text {debrisonpobe }}(\Delta t) | |
| Object: Debris | |
| P1 = 0 | P2 = 60 v2 |
| \mathrm{J}_{12}=+F_{\text {probeondebris }}(\Delta t) | |
The free-body diagrams for the two objects during this time interval are shown below.
Applying the impulse-momentum relation to each object separately yields:
| Probe | Debris |
| P_{1}+J_{12}=P_{2} | P_{1}+J_{12}=P_{2} |
| 250(5000)-F_{\text {debrisonprobe }}(\Delta t)=250 v_{2} | 0+F_{\text {probeondebris }}(\Delta t)=60 v_{2} |
| 1250000-F_{\text {debrisonprobe }}(\Delta t)=250 v_{2} | F_{\text {probeondebris }}(\Delta t)=60 v_{2} |
Notice that the final velocities of the two objects are the same, because they remain joined together following the collision. Also, the \Deltat’s are the same because the time interval over which the force of the debris acts on the probe must be the same as the time interval over which the force of the probe acts on the debris. In fact, these two forces must be equal to each other in magnitude by Newton’s Third Law.
Thus, the impulses must cancel if the two equations are added together:
\begin{array}{l} 1250000-F_{\text {debrisonprobe }}(\Delta t)=250 v_{2} \\ \underline{F_{\text {probeondebris }}(\Delta t)=60 v_{2}} \\ 1250000=310 v_{2} \\ v_{2}=4032 \mathrm{~m} / \mathrm{s} \end{array} \nonumber
The probe slows to a speed of 4032 m/s (and the debris changes direction and accelerates to a speed of 4032 m/s) via the collision. Thus, even though we do not know the magnitude of the force involved, or the duration of the collision, we can calculate the final velocities of the two objects colliding. This is because the forces involved comprise an interaction, and by Newton’s Third Law forces that comprise an interaction are always equal in magnitude and opposite in direction.
In fact, in problems involving collisions (or explosions, which to physicists are merely collisions played backward in time!), you should almost always apply the impulse-momentum relation to the interacting objects because the forces involved comprise an interaction. Thus, by adding your equations together, these terms will always add to zero. This will often allow you to determine the final velocities of the colliding objects.
In conclusion, I should point out that the probe loses momentum during the collision and that the debris gains the exact same amount of momentum. (Check the numbers to verify this statement.) The momentum is transferred from the probe to the debris through the action of the impulse the probe and debris exert on each other. The momentum transfer from the probe to the debris is analogous to throwing a wooden block from the playroom into the yard: The playroom now has one less block and the yard has one more!
Applying the Work-Energy Relation to the Same Collision
Let’s return to the collision scenario discussed above and attempt to investigate it using workenergy.
Far from the earth, a 250 kg space probe, moving at 5 km/s, collides head-on with a 60 kg piece of space debris initially at rest. The debris becomes entangled in the probe’s solar collectors.
| Event 1: The instant before the collision. | Event 2: The instant the debris and probe reach a common velocity. |
|---|---|
| Object: Space Probe | |
| \mathrm{KE}_{1}=1 / 2 \ (250) 5000^{2} | \mathrm{KE}_{2}=1 / 2 \ (250) {\mathrm{v}_{2}}^{2} |
| GE1 = 0 | GE2 = 0 |
| \mathrm{W}_{12}=F_{\text {on P }}\left(\Delta r_{P}\right) \cos 180 | |
| Object: Debris | |
| KE1 = 0 |
\mathrm{KE}_{2}=1 / 2 \ (60) {\mathrm{v}_{2}}^{2} |
| GE1 = 0 | GE2 = 0 |
| \mathrm{W}_{12}=F_{\text {on D }}\left(\Delta r_{D}\right) \cos 0 | |
Applying the work-energy relation to each object separately yields:
| Probe | Debris |
| K E_{i}+G E_{i}+W_{i f}=K E_{f}+G E_{f} | K E_{i}+G E_{i}+W_{i f}=K E_{f}+G E_{f} |
| \frac{1}{2}(250)(5000)^{2}+\left(F_{o n P}\right)\left(\Delta r_{\text {probe }}\right) \cos 180=\frac{1}{2}(250)\left(v_{2 \text { probe }}\right)^{2} | 0+\left(F_{o n D}\right)\left(\Delta r_{\text {debris }}\right) \cos 0=\frac{1}{2}(60)\left(v_{2 \text { debris}}\right)^{2} |
| 3.13 \times 10^{9}-F_{\text {onP }}\left(\Delta r_{\text {probe }}\right)=125{ v_{2 \text { probe }}}^{2} | F_{\text {onD }}\left(\Delta r_{\text {debris }}\right)=30 {v_{2 \text { debris }}}^2 |
The final velocities of the two objects are the same, because they remain joined together following the collision, and the two forces are the same by Newton’s Third Law. However, these two equations cannot be added together and solved because the two distances over which the forces act, \Delta r_{\text {probe }} and \Delta \mathbf{r}_{\text {debris }}, are not necessarily equal. During the collision, the center of the probe will move a different distance that the center of the debris3. Since these two distances are different, the works will not cancel as the impulses did, and the equations are not solvable!
3 If the two objects were actually particles, rather than being approximated as particles, then the two distances would have to be the same and the two works would cancel when the equation were added together.
In fact, since we know v2 = 4032 m/s from our momentum analysis,
| Probe | Debris |
| 3.13 \times 10^{9}-F_{\text {onP }}\left(\Delta r_{\text {probe}}\right)=125(4032)^{2} | F_{\text {onD }}\left(\Delta r_{\text {debris }}\right)=30(4032)^{2} |
| 3.13 \times 10^{9}-F_{\text {onP }}\left(\Delta r_{\text {probe }}\right)=2.03 \times 10^{9} | W_{\text {ondebris }}=F_{\text {onD }}\left(\Delta r_{\text {debris }}\right)=0.49 \times 10^{9} J |
| W_{\text {onprobe }}=-F_{\text {onP }}\left(\Delta r_{\text {probe }}\right)=-1.1 \times 10^{9} \mathrm{~J} | |
Obviously, the two works do not cancel. In fact, the internal work, or work done by the objects on each other, totals -0.61 x 109 J. This means that there is 0.61 x 109 J less kinetic energy in the system of the probe and the debris after the collision than before the collision. This is sometimes referred to as the energy lost in the collision, although the energy is not lost but rather converted into other forms of energy (i.e., other hiding places for the wooden blocks that have yet to be discussed), such as thermal energy.
In short, the work-energy relation (as it now stands) cannot be used to effectively analyze collisions unless additional information regarding the internal energy is available. Occasionally, an approximation is made in which the total internal work is zero. When this approximation is made, the collision is referred to as an elastic collision. Realistic collisions, in which the total internal energy is not zero and kinetic energy is “lost”, are referred to as inelastic collisions.
Activities
Below are momentum vs. time graphs for six different objects.
a. Rank these graphs on the basis of the change in momentum of the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. Rank these graphs on the basis of the total impulse on the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are kinetic energy vs. time graphs for six different objects. All of the objects move horizontally.
a. Rank these graphs on the basis of the change in kinetic energy of the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. Rank these graphs on the basis of the total work on the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are velocity vs. time graphs for six equal-mass objects.
a. Rank these graphs on the basis of the change in momentum of the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. Rank these graphs on the basis of the change in kinetic energy of the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are velocity vs. time graphs for six equal-mass objects. All of the objects move horizontally.
a. Rank these graphs on the basis of the total impulse on the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. Rank these graphs on the basis of the total work on the object over the time interval indicated.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Largest Negative
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are six automobiles initially traveling at the indicated velocity. The automobiles have different masses and velocities.
a. All automobiles will be stopped in the same amount of time. Rank these automobiles on the basis of the magnitude of the force needed to stop them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. All automobiles will be stopped in the same amount of distance. Rank these automobiles on the basis of the magnitude of the force needed to stop them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are six automobiles initially traveling at the indicated velocity. The automobiles have different masses and velocities.
a. Rank these automobiles on the basis of the magnitude of the force needed to stop them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
b. Rank these automobiles on the basis of the magnitude of the work needed to stop them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
c. Rank these automobiles on the basis of the magnitude of the impulse needed to stop them.
Largest Positive 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
For each of the collisions illustrated below, sketch a graph of the momentum and velocity of asteroid A, the momentum and velocity of asteroid B, and the total momentum in the system of the two asteroids. Begin your graph before the collision takes place and continue it after the collision is over. Use a consistent scale on all graphs.
a. The two asteroids remain joined together after the collision.
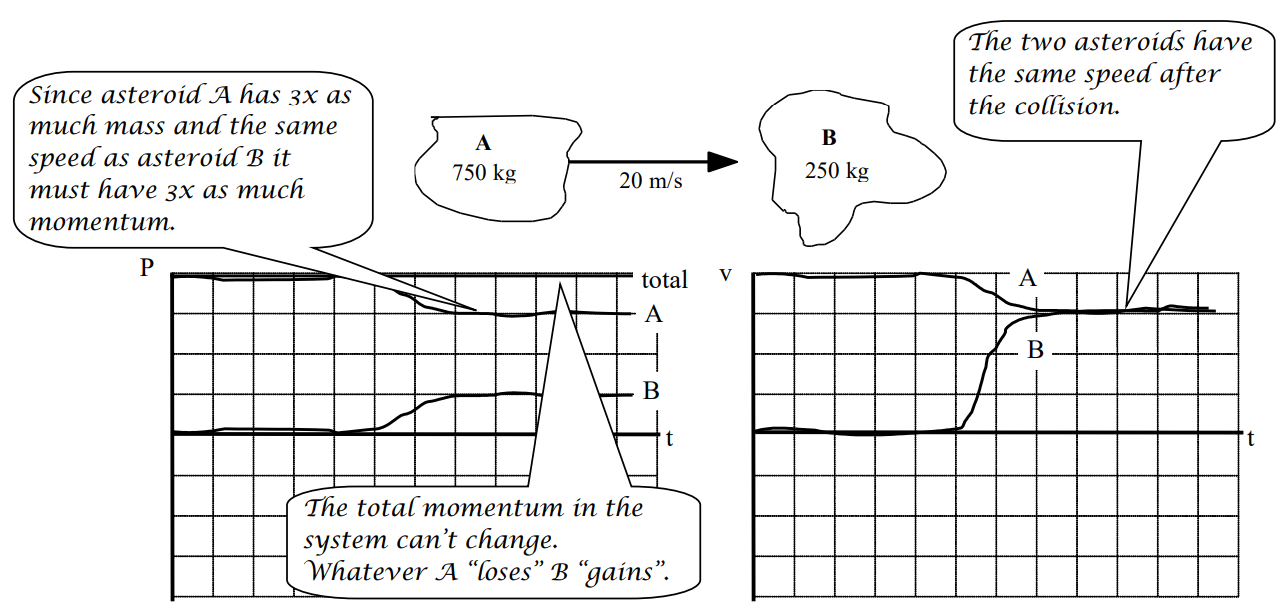
b. The two asteroids remain joined together after the collision.
For each of the collisions illustrated below, sketch a graph of the momentum and velocity of asteroid A, the momentum and velocity of asteroid B, and the total momentum in the system of the two asteroids. Begin your graph before the collision takes place and continue it after the collision is over. Use a consistent scale on all graphs.
a. The two asteroids remain joined together after the collision.
b. The two asteroids remain joined together after the collision.
For each of the collisions illustrated below, sketch a graph of the momentum and velocity of asteroid A, the momentum and velocity of asteroid B, and the total momentum in the system of the two asteroids. Begin your graph before the collision takes place and continue it after the collision is over. Use a consistent scale on all graphs.
a. The two asteroids remain joined together after the collision.
b. The two asteroids remain joined together after the collision.
For each of the collisions illustrated below, sketch a graph of the momentum and velocity of asteroid A, the momentum and velocity of asteroid B, and the total momentum in the system of the two asteroids. Begin your graph before the collision takes place and continue it after the collision is over. Use a consistent scale on all graphs.
a. Asteroid A rebounds at 5 m/s after the collision.
b. Asteroid B moves at 20 m/s after the collision.
For each of the explosions illustrated below, sketch a graph of the momentum and velocity of fragment A, the momentum and velocity of fragment B, and the total momentum in the system of the two fragments. Begin your graph before the explosion takes place and continue it while the fragments travel away from the sight of the explosion. Use a consistent coordinate system and scale on all graphs.
a. The exploding egg is initially at rest.
b. The exploding egg is initially at rest.
The exploding egg is initially at rest.
A 200 kg astronaut is initially at rest on the extreme edge of a 1000 kg space platform. She wears special magnetic shoes that allow her to walk along the metal platform. For each of the situations illustrated below, sketch a graph of the momentum and velocity of the astronaut, the momentum and velocity of the platform, and the total momentum in the system of the two objects. Begin your graph before the astronaut begins to walk and continue it while she walks along the platform. Use a consistent coordinate system and scale on all graphs.
a. The astronaut and platform are initially at rest.
b. The astronaut and platform are initially drifting to the right.
For each of the scenarios described below, indicate the amount of kinetic energy and gravitational potential energy of the object at each of the events listed. Use a consistent scale throughout each motion. Set the lowest point of the motion as the zero-point of gravitational potential energy.
a. A 4000 kg rocket’s engine produces a thrust of 70,000 N for 15 s. The rocket is fired vertically upward.
b. To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a 2.0 m thick foam cushion resting on the ground. However, he misses the cushion. The pole-vaulter sinks about 0.10 m into the ground before stopping.
For each of the scenarios described below, indicate the amount of kinetic energy and gravitational potential energy of each object at each of the events listed. Use a consistent scale throughout each motion. Set the lowest point of the motion as the zero-point of gravitational potential energy
a. Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. An 84 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the 84 kg block is released, the student is pulled up to his dorm room, 8.0 m off the ground.
b. Tired of walking down the stairs, a 75 kg engineering student designs an ingenious device for reaching the ground from his third floor dorm room. A 60 kg block at rest on the ground is attached to a rope that passes over a pulley. The student grabs the other end of the rope and steps out of his window.
A 100 kg man concerned about his weight decides to weigh himself in an elevator. He stands on a bathroom scale in an elevator that is moving upward at 3.0 m/s. As the elevator reaches his floor, it slows to a stop.
a. If the elevator slows to a stop over a distance of 2.0 m, what is the reading on the bathroom scale?
b. If the elevator slows to a stop in 1.5 s, what is the reading on the bathroom scale?
Motion Diagram
a. Motion Information
| Event 1: | Event 2: |
|---|---|
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Mathematical Analysis26
Free-Body Diagram
b. Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis
A 70 kg student is 120 m above the ground, moving upward at 3.5 m/s, while hanging from a rope hanging from a 280 kg helium balloon. The lift on the balloon due to the buoyant force is 3000 N.
a. With what speed does the student hit the ground?
b. How long does it take the student to reach the ground?
Motion Diagram
a. Motion Information
| Event 1: | Event 2: |
|---|---|
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Mathematical Analysis27
Free-Body Diagram
b. Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis
A 4000 kg rocket’s engine produces a thrust of 70,000 N for 15 s. The rocket is fired vertically upward.
a. What is the speed of the rocket when its engine turns off?
b. How long does it take the rocket to reach its maximum height?
Motion Diagram
a. Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis28
Free-Body Diagram
b. Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis
To practice falling, a 55 kg pole-vaulter falls off of a wall 6.0 m above a 2.0 m thick foam cushion resting on the ground. However, he misses the cushion. The pole-vaulter sinks about 0.10 m into the ground before stopping.
a. What is the speed of the pole-vaulter when he hits the ground?
b. What is the force exerted on the pole-vaulter by the ground as he comes to rest?
Motion Diagram
a. Motion Information
| Event 1: | Event 2: |
|---|---|
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Mathematical Analysis29
Free-Body Diagram
b. Motion Information
| Event 1: | Event 2: |
|---|---|
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Mathematical Analysis
A decorative light fixture in an elevator consists of a 2.0 kg light suspended by a cable from the ceiling of the elevator. From this light, a separate cable suspends a second 0.80 kg light. The elevator is moving downward at 4.0 m/s when someone presses the emergency stop button. During the stop, the upper cable snaps. The elevator engineer says that the cable could withstand a force of 40 N without breaking. Find the maximum time and distance over which the elevator stopped.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Mathematical Analysis30
Free-Body Diagram
Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. An 84 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the 84 kg block is released, the student is pulled up to his dorm room, 8.0 m off the ground.
Motion Diagram
Motion Information
| Event 1: The block is released | Event 2: The student reaches the room. |
|---|---|
| Object: Student | |
| KE1 = 0 | KE2 = 1 / 2(80) \mathcal{V}_{f}^{2} |
| GE1 = 0 | GE2 = 80(9.8)(8) |
| W12 = \mathcal{F}_{\mathrm{R}}(8) \cos 0^{\circ} | |
| Object: Block | |
| KE1 = 0 | KE2 = 1 / 2(84) \mathcal{V}_{f}^{2} |
| GE1 = 84(9.8)(8) | GE2 = 0 |
| W12 = \mathcal{F}_{R}(8) \cos 180^{\circ} | |
Free-Body Diagram
Since the distance the student and block travel is known, applying work-energy should allow us to solve the problem. I’ll apply it separately to each object.
| student | block |
|---|---|
| 0+F_{\text {rope }}(8)=\frac{1}{2} 80 v_{f}^{2}+80(9.8)(8) | 84(9.8)(8)-F_{\text {rope }}(8)=\frac{1}{2} 84 v_{f}^{2} |
| 8 F_{\text {rope }}=40 v_{f}^{2}+6272 | 6586-8 F_{\text {rope }}=42 v_{f}^{2} |
\mathcal{F}_{\text {rope }} is the same in both equations, as is the final speed. Thus the two equations can be added together to yield:
\begin{aligned} &6586=40 v_{f}^{2}+42 v_{f}^{2}+6272 \\ &314=82 v_{f}^{2} \\ &v_{f}=1.96 \mathrm{~m} / \mathrm{s} \end{aligned} \nonumber
Notice that if you applied work-energy to the entire system you would have generated this same equation. Initially, the only form of energy present is the gravitational energy of the block (mgh = 6586 J). At the second event, both objects have kinetic energy plus the student has gravitational potential energy (mgh = 6272 J).
Tired of walking up the stairs, an engineering student designs an ingenious device for reaching his third floor dorm room. A 100 kg block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room, 8.0 m off the ground. He is traveling at 2.2 m/s when he reaches his room.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
| Object: | |
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Free-Body Diagram
Mathematical Analysis31
Tired of walking down the stairs, a 75 kg engineering student designs an ingenious device for reaching the ground from his third floor dorm room. A 60 kg block at rest on the ground is attached to a rope that passes over a pulley. The student grabs the other end of the rope and steps out of his window. He falls for 5.5 s before reaching the ground.
Motion Diagram
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Free-Body Diagram
Mathematical Analysis32
Tired of walking down the stairs, a 75 kg engineering student designs an ingenious device for reaching the ground from his dorm room. A 60 kg block at rest on the ground is attached to a rope that passes over a pulley. The student grabs the other end of the rope and steps out of his window. He hits the ground at 3.3 m/s.
Motion Diagram
Motion Information
| Event 1: | Event 2: | ||
|---|---|---|---|
| Object: | Object: | ||
| P1 = | P2 = | P1 = | P2 = |
| J12 = | J12 = | ||
| P1 = | P2 = | P1 = | P2 = |
| KE1 = | KE2 = | KE1 = | KE2 = |
| GE1 = | GE2 = | GE1 = | GE2 = |
| W12 = | W12 = | ||
Free-Body Diagram
Mathematical Analysis33
Far from any other masses, a 2000 kg asteroid traveling at 12 m/s collides with a 1200 kg asteroid traveling in the other direction at 16 m/s. After the collision they remain joined together and move with a common velocity.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis34
On a remote stretch of intergalactic highway, a 7.5 x 106 kg spaceship traveling at 10 percent the speed of light (0.10c = 3.0 x 107 m/s) doesn’t notice the slower spaceship ahead clogging the lane. The fast-moving ship rear-ends the slower ship, an older 5.5 x 106 kg model, and the two ships get entangled and drift forward at 0.07c.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis35
On a remote stretch of intergalactic highway, a 7.5 x 106 kg spaceship traveling at 10 percent the speed of light (0.10c = 3.0 x 107 m/s) doesn’t notice the slower spaceship ahead, moving at 0.05c, clogging the lane. The fast-moving ship rear-ends the slower ship, an older 4.5 x 106 kg model, and the slower ship gets propelled forward at 0.13c.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis36
In the farthest reaches of deep space, an 8000 kg spaceship, including contents, is at rest relative to a space station. The spaceship recoils after it launches a 600 kg scientific probe with a speed of 300 m/s relative to the space station.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis37
In the farthest reaches of deep space, an 8000 kg spaceship, including contents, is drifting at 50 m/s relative to a space station. The spaceship is brought to rest, relative to the space station, by the recoil from launching a 600 kg scientific probe.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis38
A 140 kg astronaut is standing on the extreme edge of a 1000 kg space platform, at rest relative to the mother ship. She begins to walk toward the other edge of the platform, reaching a speed of 2.0 m/s relative to the mother ship. (She wears special magnetic shoes that allow her to walk along the metal platform.)
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis39
Two astronauts, 140 kg Andy and 170 kg Bob, are standing on opposite edges of a 1000 kg space platform, at rest relative to the mother ship. They each begin to walk toward the opposite ends of the platform, Andy reaching a speed of 2.0 m/s and Bob 1.5 m/s, both relative to the mother ship. (They wear special magnetic shoes that allow them to walk along the metal platform.)
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis40
A 70 kg student is hanging from a 280 kg helium balloon. The balloon is rising at a constant speed of 8.0 m/s relative to the ground. The lift on the balloon due to the buoyant force is constant. The student begins to climb up the rope at a speed of 15 m/s relative to the ground. The balloon's upward speed is decreased as the student climbs.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Mathematical Analysis41
A man of mass m, concerned about his weight, decides to weigh himself in an elevator. He stands on a bathroom scale in an elevator which is moving upward at v. As the elevator reaches his floor, it slows to a stop over a time interval, T. Determine the reading on the bathroom scale (Fscale) as a function of m, v, T, and g.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
Questions
If T = ∞, what should Fscale equal? Does your function agree with this observation?
For what combination of v and T would the bathroom scale read 0 N?
If the elevator were initially going down, would the above combination of v and T also lead to a scale reading of 0 N?
A rocket of mass m is fired vertically upward from rest. The rocket’s engine produces a thrust of constant magnitude F for tthrust seconds. Determine the time it takes the rocket to reach its apex (tapex) as a function of F, tthrust, m, and g.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| P1 = | P2 = |
| J12 = | |
Questions
If g = 0 m/s2, what should tapex equal? Does your function agree with this observation?
If F = mg, what should tapex equal? Does your function agree with this observation?
For what value of F would tapex = 2tthrust?
To practice falling, a pole-vaulter of mass m falls off of a wall a distance D above a thick foam cushion. The pole-vaulter sinks a distance d into the cushion before stopping. Determine the force exerted on the pole-vaulter due to the cushion (Fcushion) as a function of m, D, d, and g.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Questions
If D = ∞, what should Fcushion equal? Does your function agree with this observation?
If d = 0 m, what should Fcushion equal? Does your function agree with this observation?
What would be worse for the pole-vaulter, starting at twice the initial distance above the cushion or sinking half of the original distance into the cushion?
Tired of walking up the stairs, an engineering student of mass m designs an ingenious device for reaching his third floor dorm room. A block of mass M is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room in a time T. Determine the velocity of the student (v) when he reaches his room as a function of m, M, T and g.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Questions
If g = 0 m/s2, what should v equal? Does your function agree with this observation?
If m = M, what should v equal? Does your function agree with this observation?
If M = ∞, what should v equal? Does your function agree with this observation?
Tired of walking down the stairs, an engineering student of mass m designs an ingenious device for reaching the ground from her dorm room. A block of mass M at rest on the ground is attached to a rope that passes over a pulley. The student grabs the other end of the rope and steps out of her window a distance D above the ground. Determine the velocity of the student (v) when she reaches the ground as a function of m, M, D and g.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
| Object: | |
| KE1 = | KE2 = |
| GE1 = | GE2 = |
| W12 = | |
Questions
If g = 0 m/s2, what should v equal? Does your function agree with this observation?
If m = M, what should v equal? Does your function agree with this observation?
If M = ∞, what should v equal? Does your function agree with this observation?
In the farthest reaches of deep space, a spaceship of mass M, including contents, is at rest relative to a space station. The spaceship recoils after it launches a scientific probe of mass m at a speed v relative to the space station. Determine the recoil speed of the spaceship (V) as a function of M, m, and v.
Motion Diagram
Free-Body Diagrams
Motion Information
| Event 1: | Event 2: |
|---|---|
| Object: | |
| P1 = | P2 = |
| J12 = | |
| Object: | |
| P1 = | P2 = |
| J12 = | |
Questions
If M = 2m, what should V equal? Does your function agree with this observation?
If M = ∞, what should V equal? Does your function agree with this observation?
Model One
Summary Problems
- A sprinter in a 100 meter dash starts from rest and accelerates at 2.5 m/s2 for 3.9 s. She then runs at a constant speed, until she either tires or finishes the race. She can run at a constant velocity for at most 7.0 s without tiring. Once tired, she begins to slow, accelerating at 1.0 m/s2. How long does it take her to finish the race?
- The Schindler Mobile is a self-propelled elevator, powered by a small motor attached to the bottom of the elevator cab that drives the cab up and down the tracks of two high-strength aluminum columns. Assume the Schindler Mobile can travel from the 1st floor to the 10th floor (approximately 40 m) in 15 s. Assume the elevator both speeds up and slows
- The Thrust SSC, a 7 ton jet mobile powered by two Royal Air Force Phantom jets providing 110,000 hp, was designed to break the speed of sound. The "car" was tested at a 15 mile long track in the Black Rock desert of Nevada. The car accelerated for nearly five miles, then moved through a measured mile at top speed. The car slowed by cutting power and releasing parachutes for five additional miles before applying brakes at speeds below 300 mph. Complete a kinematic description for the car's motion, assuming it reaches a maximum speed of Mach 1 (750 mph at the temperatures encountered at the Black Rock desert raceway).
- Often the reason for the formation of congested traffic is obvious; accidents, lane closings, or other bottlenecks. However, you have probably also experienced "phantom" traffic jams, which emerge without any obvious reason, seemingly out of nothing. This phenomenon can be understood by the collective behavior of many drivers. If one vehicle drives more slowly than others, the vehicle behind has to brake to maintain the desired safety time. (The safety time is the elapsed time between the two objects passing the same point. Thus, the distance associated with this "time cushion" varies with the speed of the traffic.) Consequently, the next vehicle behind has to brake, and so on. If traffic flow is unstable, each following vehicle has to brake stronger than its predecessor. Thus, a small initial perturbation triggers a backward propagating "wave" of slower vehicles with increasing amplitude. Finally, the vehicles come nearly to a stop; a full-fledged traffic jam has evolved. The driver having caused the small perturbation by driving unusually slowly escapes without even realizing what he has triggered!
To get a better feel for the kinematics involved in instigating phantom jams, imagine a car approaching a slow-moving truck on a one-lane road. The car is initially traveling at 120 km/hr, while the truck moves at 70 km/hr. The car is 100 m behind the truck when the driver first notices the truck. Find the minimum acceleration necessary for the car to come to equilibrium behind the truck and achieve a safety time of 2 s. Assume the truck does not accelerate. - When modeling traffic flow, various psychological factors must be incorporated. One is the politeness factor. The politeness factor quantifies how much one weights disadvantages imposed on other drivers against one's own advantage when considering a lane change. Lane changes are more common when the politeness factor is low. Different regions of the country have, on average, different politeness factors. In addition, urban vs. rural drivers differ in politeness factor. At high values of the politeness factor, drivers run the risk of getting stuck permanently behind slow-moving vehicles or other obstacles.
To get a better feel for how "politeness" affects traffic flow, imagine a car stuck behind a 5 m long, stationary obstacle blocking its lane. 30 m ahead of the car is a turn in the road. Therefore, the driver of the car cannot see an approaching car or truck until it is 30 m from the car.- If the car pulls out to go around the obstacle (with acceleration 4 m/s2) just as a truck moving at 55 mph rounds the bend, is this an “extremely polite" maneuver? (A maneuver is extremely polite when the truck does not need to slow down in order to avoid an accident.)
- What acceleration is necessary for an extremely polite driver to pull out from behind the barrier? (If the car cannot generate this acceleration, an extremely polite driver must spend the rest of their life stuck behind the barrier!)
- Traffic engineers are concerned with selecting the proper "yellow time" to ensure safe passage through stoplights. To understand this scenario, imagine yourself driving down a relatively empty road. Up ahead, the traffic light turns yellow. If you are close enough to the traffic light you can pass through the intersection before the light turns red. If you are far from the traffic light you can safely slow down and stop before the intersection. But what if you are in-between, in what is termed the "no-win" zone, and are too far to make it and too close to stop? Traffic engineers design the duration of the yellow signal to eliminate this no-win zone.
- You are driving at the speed limit (45 mph) on a straight, empty road with perfect visibility. Your maximum acceleration while braking is 7.0 m/s2. The yellow time is 1.0 s. Determine the location of the no-win zone (i.e., the range of positions from which you cannot safely traverse the intersection). Assume you don't speed up to "run" the yellow, since this is an illegal activity.
- If you do want to "run" the yellow from anywhere in the no-win zone, what minimum acceleration is needed? Is this feasible? How fast would you be traveling as you go through the intersection?
- Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching his third floor dorm room. A heavy block is attached to a rope that passes over a pulley. The student holds the other end of the rope. When the block is released, the student is pulled up to his dorm room, 8.0 m off the ground. However, the student has a weak stomach and will get nauseous if he accelerates at greater than 4.0 m/s2. Also, the rope he used can transmit a force of only 1100 N before breaking. If possible, what mass ballast block should he use to avoid breaking the rope and avoid getting nauseous?
- Tired of walking up the stairs, an 80 kg engineering student designs an ingenious device for reaching her third floor dorm room. A heavy block is attached to a rope that passes over a pulley. The student holds the other end of the rope. However, the dorm room window is 12 m off the ground and the block is initially only 10 m off the ground. The student wants to choose a mass for the block such that when the block hits the ground, the student is “launched” upward, and reaches her window at the apex of her motion. (That will make it easiest to climb in the window.) What mass block should she use?
- Selected Answers
-
1 r2 = 1.4 m
2 t2 = 1.45 m
3 t3 = 3.4 s
4 t3 = 4.55 s
5 r3 = 36.6 m
6 r3 = 3520 m
7 r2 = 14.9 m
8 r4 = 2000 m
9 t4 = 3.7 x 105 s
10 t2 = 14.9 s
11 t2 = 7.8 s
12 t3 = 15.7 s
13 t3 = 2.87 s
14 F rope = 420 N
15 F cushion = 1910 N
16 a ≥ 4.49 m/s2
17 t2 = 17.1 s to reach ground
18 F cushion = 2830 N
19 F ground = 43700 N
20 r3 = 63.5 m
21 r3 = 1550 m
22 m block = 240 kg
23 m block = 26 kg
24 F rope = 500 N
25 F rope = 466 N
26 a. F scale = 755 N b. F scale = 780 N
27 a. v = 17.5 m/s b. t = 17.1 s
28 a. v = 116 m/s b. t = 26.8 s
29 a. v = 12.5 m/s b. F ground = 43700 N
30 t2 = 0.89 s r2 = 1.78 m
31 m student = 94 kg
32 v2 = 6.0 m/s
33 Student falls 5.0 m in 3.03 s
34 v2 = 1.5 m/s
35 v1 slowship = 0.029c = 8.73 x 106 m/s
36 v2 fastship = 0.052c = 1.56 x 107 m/s
37 v2 ship = 24.3 m/s
38 v probe = 667 m/s
39 v2 platform = 0.28 m/s
40 v2 platform = 0.025 m/s
41 v2 balloon = 6.3 m/s


