9.4: Bonding in Crystalline Solids
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the packing structures of common solids
- Explain the difference between bonding in a solid and in a molecule
- Determine the equilibrium separation distance given crystal properties
- Determine the dissociation energy of a salt given crystal properties
Beginning in this section, we study crystalline solids, which consist of atoms arranged in an extended regular pattern called a lattice. Solids that do not or are unable to form crystals are classified as amorphous solids. Although amorphous solids (like glass) have a variety of interesting technological applications, the focus of this chapter will be on crystalline solids.
Atoms arrange themselves in a lattice to form a crystal because of a net attractive force between their constituent electrons and atomic nuclei. The crystals formed by the bonding of atoms belong to one of three categories, classified by their bonding: ionic, covalent, and metallic. Molecules can also bond together to form crystals; these bonds, not discussed here, are classified as molecular. Early in the twentieth century, the atomic model of a solid was speculative. We now have direct evidence of atoms in solids (Figure 9.4.1).
Ionic Bonding in Solids
Many solids form by ionic bonding. A prototypical example is the sodium chloride crystal, as we discussed earlier. Electrons transfer from sodium atoms to adjacent chlorine atoms, since the valence electrons in sodium are loosely bound and chlorine has a large electron affinity. The positively charged sodium ions and negatively charged chlorine (chloride) ions organize into an extended regular array of atoms (Figure 9.4.2).
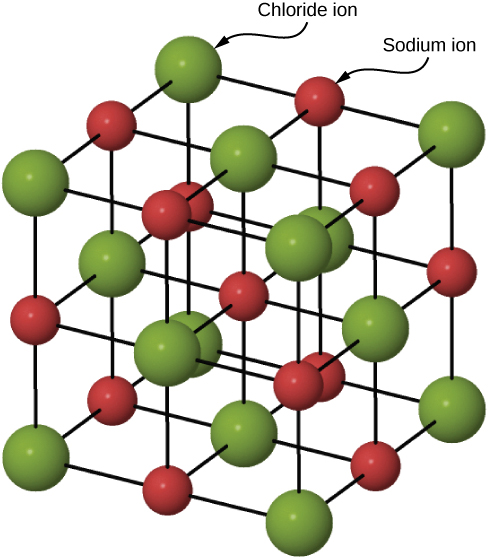
The charge distributions of the sodium and chloride ions are spherically symmetric, and the chloride ion is about two times the diameter of the sodium ion. The lowest energy arrangement of these ions is called the face-centered cubic (FCC) structure. In this structure, each ion is closest to six ions of the other species. The unit cell is a cube—an atom occupies the center and corners of each “face” of the cube. The attractive potential energy of the Na+ ion due to the fields of these six Cl− ions is written
U1=−6e24πϵ0r
where the minus sign designates an attractive potential (and we identify k=1/4πϵ0). At a distance √2r are its next-nearest neighbors: twelve Na+ ions of the same charge. The total repulsive potential energy associated with these ions is
U2=12e24πϵ0√2r.
Next closest are eight Cl− ions a distance 3√r3r from the Na+ ion. The potential energy of the Na+ ion in the field of these eight ions is
U3=−8e24πϵ0√3r.
Continuing in the same manner with alternate sets of Cl− and Na+ ions, we find that the net attractive potential energy UA of the single Na+ ion can be written as
Ucoul=−αe24πϵ0r
where α is the Madelung constant, introduced earlier. From this analysis, we can see that this constant is the infinite converging sum
α=6−12sqrt2+8√3+...
Distant ions make a significant contribution to this sum, so it converges slowly, and many terms must be used to calculate αα accurately. For all FCC ionic solids, αα is approximately 1.75.
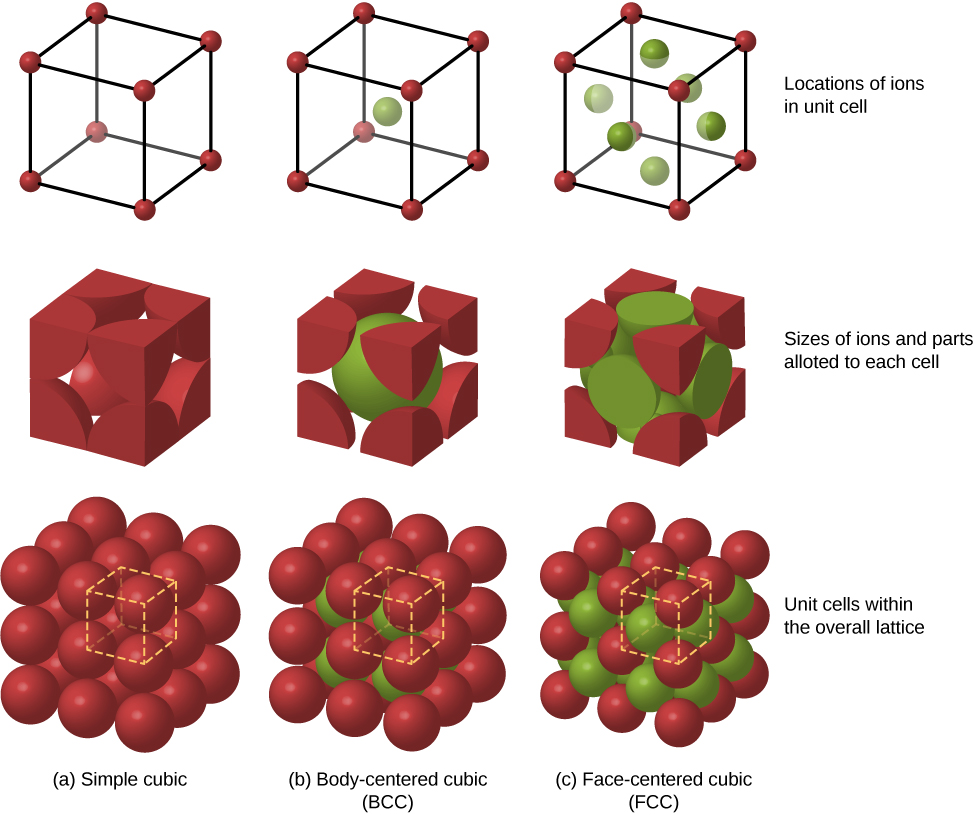
Other possible packing arrangements of atoms in solids include simple cubic and body-centered cubic (BCC). These three different packing structures of solids are compared in Figure 9.4.3. The first row represents the location, but not the size, of the ions; the second row indicates the unit cells of each structure or lattice; and the third row represents the location and size of the ions. The BCC structure has eight nearest neighbors, with a Madelung constant of about 1.76—only slightly different from that for the FCC structure. Determining the Madelung constant for specific solids is difficult work and the subject of current research.
The energy of the sodium ions is not entirely due to attractive forces between oppositely charged ions. If the ions are bought too close together, the wave functions of core electrons of the ions overlap, and the electrons repel due to the exclusion principle. The total potential energy of the Na+ ion is therefore the sum of the attractive Coulomb potential (Ucoul) and the repulsive potential associated with the exclusion principle (Uex). Calculating this repulsive potential requires powerful computers. Fortunately, however, this energy can be described accurately by a simple formula that contains adjustable parameters:
Uex=Arn
where the parameters A and n are chosen to give predictions consistent with experimental data. For the problem at the end of this chapter, the parameter n is referred to as the repulsion constant. The total potential energy of the Na+ ion is therefore
U=−αe24πϵ0r+Arn.
At equilibrium, there is no net force on the ion, so the distance between neighboring Na+ and Cl− ions must be the value r0 for which U is a minimum. Setting dUdr=0, we have
0=αe24πϵ0r20−nArn+10.
Thus,
A=αe2rn−104πϵ0n.
Inserting this expression into the expression for the total potential energy, we have
U=−αe24πϵ0r0[r0r−1n(r0r)n].Notice that the total potential energy now has only one adjustable parameter, n. The parameter A has been replaced by a function involving r0r0, the equilibrium separation distance, which can be measured by a diffraction experiment (you learned about diffraction in a previous chapter). The total potential energy is plotted in Figure 9.4.4 for n=0, the approximate value of n for NaCl.
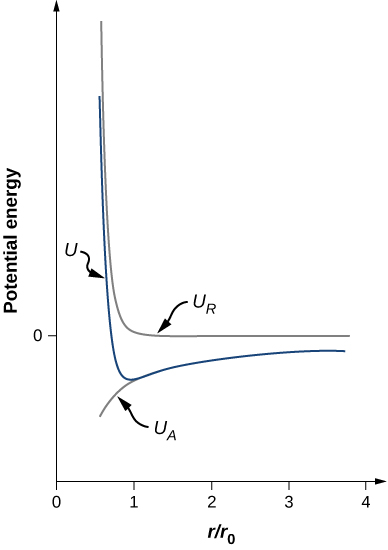
As long as n>1, the curve for U has the same general shape: U approaches infinity as r→0 and U approaches zero as r→∞. The minimum value of the potential energy is given by
Umin(r=r0)=−αfe2r0(1−1n).
The energy per ion pair needed to separate the crystal into ions is therefore
Udiss=αke2r0(1−1n).
This is the dissociation energy of the solid. The dissociation energy can also be used to describe the total energy needed to break a mole of a solid into its constituent ions, often expressed in kJ/mole. The dissociation energy can be determined experimentally using the latent heat of vaporization. Sample values are given in the following table.
| F− | Cl− | Br− | I− | |
|---|---|---|---|---|
| Li+ | 1036 | 853 | 807 | 757 |
| Na+ | 923 | 787 | 747 | 704 |
| K+ | 821 | 715 | 682 | 649 |
| Rb+ | 785 | 689 | 660 | 630 |
| Cs+ | 740 | 659 | 631 | 604 |
Thus, we can determine the Madelung constant from the crystal structure and n from the lattice energy. For NaCl, we have r0=2.81A, n≈8, and Udiss=7.84eV/ionpair. This dissociation energy is relatively large. The most energetic photon from the visible spectrum, for example, has an energy of approximately
hf=(4.14×10−15eV⋅s)(7.5×1014Hz)=3.1eV.
Because the ions in crystals are so tightly bound, ionic crystals have the following general characteristics:
- They are fairly hard and stable.
- They vaporize at relatively high temperatures (1000 to 2000 K).
- They are transparent to visible radiation, because photons in the visible portion of the spectrum are not energetic enough to excite an electron from its ground state to an excited state.
- They are poor electrical conductors, because they contain effectively no free electrons.
- They are usually soluble in water, because the water molecule has a large dipole moment whose electric field is strong enough to break the electrostatic bonds between the ions.
Determine the dissociation energy of sodium chloride (NaCl) in kJ/mol. (Hint: The repulsion constant n of NaCl is approximately 8.)
Strategy
A sodium chloride crystal has an equilibrium separation of 0.282 nm. (Compare this value with 0.236 nm for a free diatomic unit of NaCl.) The dissociation energy depends on the separation distance, repulsion constant, and Madelung constant for an FCC structure. The separation distance depends in turn on the molar mass and measured density. We can determine the separation distance, and then use this value to determine the dissociation energy for one mole of the solid.
Solution
The atomic masses of Na and Cl are 23.0 u and 58.4 u, so the molar mass of NaCl is 58.4 g/mol. The density of NaCl is 2.16g/cm3. The relationship between these quantities is
ρ=MV=M2NAr30,
where M is the mass of one mole of salt, NANA is Avogadro’s number, and r0r0 is the equilibrium separation distance. The factor 2 is needed since both the sodium and chloride ions represent a cubic volume r30. Solving for the distance, we get
r30=M2NAρ=58.4g/mol2(6.03×1023)(2.160g/cm3)=2.23×10−23cm3, or
r0=2.80×10−8cm=0.280nm.
The potential energy of one ion pair (Na+Cl−) is
U=−αke2r0(1−1n),
where α is the Madelung constant, r0 is the equilibrium separation distance, and n is the repulsion constant. NaCl is FCC, so the Madelung constant is α=1.7476. Substituting these values, we get
U=−1.751.44eV⋅nm0.280nm(1−18)=−7.88eVionpair.
The dissociation energy of one mole of sodium chloride is therefore
D=(7.88eVionpair)(23.052kcal1mol1eVionpair)=182kcal/mol=760kJ/mol.
Significance
This theoretical value of the dissociation energy of 766 kJ/mol is close to the accepted experimental value of 787 kJ/mol. Notice that for larger density, the equilibrium separation distance between ion pairs is smaller, as expected. This small separation distance drives up the force between ions and therefore the dissociation energy. The conversion at the end of the equation took advantage of the conversion factor 1kJ=0.239kcal.
If the dissociation energy were larger, would that make it easier or more difficult to break the solid apart?
- Answer
-
more difficult
Covalent Bonding in Solids
Crystals can also be formed by covalent bonding. For example, covalent bonds are responsible for holding carbon atoms together in diamond crystals. The electron configuration of the carbon atom is 1s22s22p2 - a He core plus four valence electrons. This electron configuration is four electrons short of a full shell, so by sharing these four electrons with other carbon atoms in a covalent bond, the shells of all carbon atoms are filled. Diamond has a more complicated structure than most ionic crystals (Figure 9.4.5). Each carbon atom is the center of a regular tetrahedron, and the angle between the bonds is 110°.110°. This angle is a direct consequence of the directionality of the p orbitals of carbon atoms.
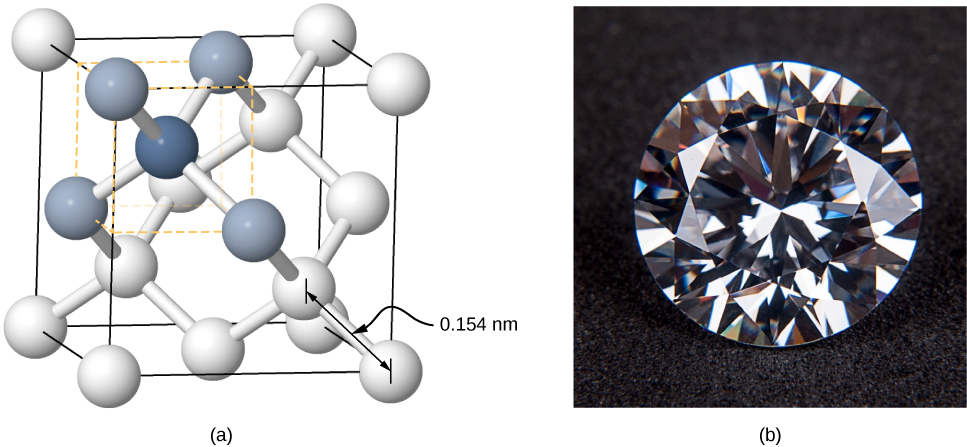
Covalently bonded crystals are not as uniform as ionic crystals but are reasonably hard, difficult to melt, and are insoluble in water. For example, diamond has an extremely high melting temperature (4000 K) and is transparent to visible light. In comparison, covalently bonded tin (also known as alpha-tin, which is nonmetallic) is relatively soft, melts at 600 K, and reflects visible light. Two other important examples of covalently bonded crystals are silicon and germanium. Both of these solids are used extensively in the manufacture of diodes, transistors, and integrated circuits. We will return to these materials later in our discussion of semiconductors.
Metallic Bonding in Solids
As the name implies, metallic bonding is responsible for the formation of metallic crystals. The valence electrons are essentially free of the atoms and are able to move relatively easily throughout the metallic crystal. Bonding is due to the attractive forces between the positive ions and the conduction electrons. Metallic bonds are weaker than ionic or covalent bonds, with dissociation energies in the range 1−3eV.


