9.2: Types of Molecular Bonds
- Page ID
- 4541
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Distinguish between the different types of molecular bonds
- Determine the dissociation energy of a molecule using the concepts ionization energy, electron affinity, and Coulomb force
- Describe covalent bonding in terms of exchange symmetry
- Explain the physical structure of a molecule in terms of the concept of hybridization
Quantum mechanics has been extraordinarily successful at explaining the structure and bonding in molecules, and is therefore the foundation for all of chemistry. Quantum chemistry, as it is sometimes called, explains such basic questions as why \(H_2O\) molecules exist, why the bonding angle between hydrogen atoms in this molecule is precisely 104.5°, and why these molecules bind together to form liquid water at room temperature. Applying quantum mechanics to molecules can be very difficult mathematically, so our discussion will be qualitative only.
As we study molecules and then solids, we will use many different scientific models. In some cases, we look at a molecule or crystal as a set of point nuclei with electrons whizzing around the outside in well-defined trajectories, as in the Bohr model. In other cases, we employ our full knowledge of quantum mechanics to study these systems using wave functions and the concept of electron spin. It is important to remember that we study modern physics with models, and that different models are useful for different purposes. We do not always use the most powerful model, when a less-powerful, easier-to-use model will do the job.
Types of Bonds
Chemical units form by many different kinds of chemical bonds. An ionic bond forms when an electron transfers from one atom to another. A covalent bond occurs when two or more atoms share electrons. A van der Waals bond occurs due to the attraction of charge-polarized molecules and is considerably weaker than ionic or covalent bonds. Many other types of bonding exist as well. Often, bonding occurs via more than one mechanism. The focus of this section is ionic and covalent bonding.
Ionic bonds
The ionic bond is perhaps the easiest type of bonding to understand. It explains the formation of salt compounds, such as sodium chloride, \(\ce{NaCl}\). The sodium atom (symbol Na) has the same electron arrangement as a neon atom plus one 3s electron. Only 5.14 eV of ionization energy is required to remove this one electron from the sodium atom. Therefore, Na can easily give up or donate this electron to an adjacent (nearby) atom, attaining a more stable arrangement of electrons. Chlorine (symbol Cl) requires just one electron to complete its valence shell, so it readily accepts this electron if it is near the sodium atom. We therefore say that chlorine has a large electron affinity, which is the energy associated with an accepted electron. The energy given up by the chlorine atom in this process is 3.62 eV. After the electron transfers from the sodium atom to the chlorine atom, the sodium atom becomes a positive ion and the chlorine atom becomes a negative ion.
This reaction looks like this
\[\ce{Na(g) + Cl(g) -> Na^{+}(g) + Cl^{-}(g)} \label{rx1} \]
and the total energy required for this transfer is given by
\[E_{transfer} = 5.14 \,\text{eV} - 3.62 \,\text{eV} = 1.52 \,\text{eV}. \label{9.1} \]
The positive sodium ion and negative chloride ion experience an attractive Coulomb force. The potential energy associated with this force is given by
\[U_{coul} = -\dfrac{ke^2}{r_0}, \nonumber \]
where \(ke^2 = 1.440\, \text{eV-nm}\) and \(r_0\) is the distance between the ions.
As the sodium and chloride ions move together (“descend the potential energy hill”), the force of attraction between the ions becomes stronger. However, if the ions become too close, core-electron wave functions in the two ions begin to overlap. Due to the exclusion principle, this action promotes the core electrons—and therefore the entire molecule—into a higher energy state.
\[\ce{ Na^{+}(g) + Cl^{-}(g) -> NaCl(g)} \label{rx2} \]
The equilibrium separation distance (or bond length) between the ions occurs when the molecule is in its lowest energy state. For diatomic \(\ce{NaCl}\), this distance is 0.236 nm. Figure \(\PageIndex{1}\) shows the total energy of \(\ce{NaCl}\) as a function of the distance of separation between ions.
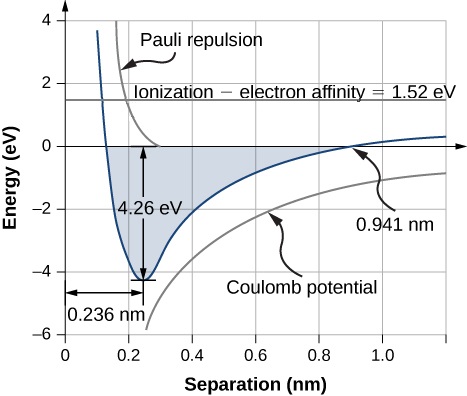
The total energy required to form a single salt unit from neutral \(\ce{Na}\) and \(\ce{Cl}\) atoms is the sum of the energies associated with electron transfer (Equation \ref{rx1}) and ion combination (Equation \ref{rx2}):
\[U_{form} = E_{transfer} + U_{coul} + U_{ex}, \nonumber \]
where \(U_{ex}\) is the energy associated with the repulsion between core electrons due to Pauli’s exclusion principle. The value of \(U_{form}\) must be negative for the bond to form spontaneously (otherwise, it is lower in energy to be separated species). The dissociation energy is defined as the energy required to separate the unit into its constituent ions, written
\[U_{diss} = -U_{form} \nonumber \]
Every diatomic formula unit has its own characteristic dissociation energy and equilibrium separation length. Sample values are given in Table \(\PageIndex{1}\).
Bonds can be broken symmetrically or asymmetrically. The former is called homolysis and is the basis of the usual (homolytic) bond dissociation energy. For the salt formula unit (\(\ce{NaCl}\)), the associated homolytic reaction would be
\[\ce{NaCl(g) -> Na (g) + Cl(g)} \label{homo} \]
The asymmetric scission of a bond is called heterolysis (i.e., heterolytic bond dissociation energy). The associated heterolytic reaction for \(\ce{ NaCl}\) would be
\[\ce{NaCl(g) -> Na^{+} (g) + Cl^{-}(g)} \label{hetero} \]
The difference in homolytic and heterolytic bond dissociation energies is just \(E_{transfer}\) given by Equation \ref{9.1}.
| Molecule | Dissociation Energy(eV) | Equilibrium Separation (nm) (Bond length) |
|---|---|---|
| NaCl | 4.26 | 0.236 |
| NaF | 4.99 | 0.193 |
| NaBr | 3.8 | 0.250 |
| NaI | 3.1 | 0.271 |
| NaH | 2.08 | 0.189 |
| LiCl | 4.86 | 0.202 |
| LiH | 2.47 | 0.239 |
| LiI | 3.67 | 0.238 |
| KCl | 4.43 | 0.267 |
| KBr | 3.97 | 0.282 |
| RbF | 5.12 | 0.227 |
| RbCl | 4.64 | 0.279 |
| CsI | 3.57 | 0.337 |
| H-H | 4.5 | 0.075 |
| N-N | 9.8 | 0.11 |
| O-O | 5.2 | 0.12 |
| F-F | 1.6 | 0.14 |
| Cl-Cl | 2.5 | 0.20 |
What is the dissociation energy of a salt formula unit (NaCl)?
Strategy
Sodium chloride (\(\ce{NaCl}\)) is a salt formed by ionic bonds. The energy change associated with this bond depends on three main processes:
- the ionization of Na and the acceptance of the electron from a Na atom by a Cl atom; and
- Coulomb attraction of the resulting ions (\(\ce{Na^{+}}\) and \(\ce{Cl^{-}}\)).
- If the ions get too close, they repel due to the exclusion principle (0.32 eV).
The equilibrium separation distance is \(r_0 = 0.236 \text{nm}\).
Solution
The energy change associated with the transfer of an electron from Na to Cl is 1.52 eV (Equation \ref{9.1}). At equilibrium separation, the atoms are \(r_0 = 0.236 \text{nm}\) apart. The electrostatic potential energy of the atoms is
\[\begin{align*} U_{could} &= -\dfrac{ke^2}{r_0} \\[5pt] &= - \dfrac{1.44 \, \text{eV} \cdot nm}{0.236 \,nm} \\[5pt] &= - 6.10 \, \text{eV} . \end{align*} \nonumber \]
The total energy difference associated with the formation of a NaCl formula unit is
\[\begin{align*}E_{form} &= E_{transfer} + U_{coul} + U_{ex} \\[5pt] &= 1.52 \, \text{eV} + (−6.10 eV) + 0.32\, \text{eV} \\[5pt] &= -4.26 eV \end{align*} \nonumber \]
Therefore, the homolytic dissociation energy of \(\ce{NaCl}\) is 4.26 eV.
Significance
The formation of a NaCl formula unit by ionic bonding is energetically favorable. The dissociation energy, or energy required to separate the NaCl unit into \(Na\) and \(Cl\) atoms is 4.26 eV, consistent with Figure \(\PageIndex{1}\).
Why is the potential energy associated with the exclusion principle positive in Example \(\PageIndex{1}\)?
- Answer
-
It corresponds to a repulsive force between core electrons in the ions.
At what \(\ce{Na}\)-\(\ce{Cl}\) distance is it energetically favorable for this reaction to occur?
\[\ce{Na(g) + Cl(g) -> Na^{+}(g) + Cl^{-}(g)} \nonumber \]
- Answer
-
This happens when the electric potential energy (\(U_{coul}\)) and Pauli repulsion energy (\(U_{ex}\)) equation the energy for the electron transfer (\(E_{transfer}\)), which is 0.941 nm as according to Figure \(\PageIndex{1}\). Note that \(U_{ex} \approx 0\) at this distance.
For a sodium ion in an ionic NaCl crystal, the expression for Coulomb potential energy \(U_{could}\) must be modified by a factor known as the Madelung constant. This factor takes into account the interaction of the sodium ion with all nearby chloride and sodium ions. The Madelung constant for a NaCl crystal is about 1.75. This value implies an equilibrium separation distance between \(Na^+\) and \(Cl^-\) ions of 0.280 nm—slightly larger than for diatomic NaCl. We will return to this point again later.
Covalent Bonds
In an ionic bond, an electron transfers from one atom to another. However, in a covalent bond, an electron is shared between two atoms. The ionic bonding mechanism cannot explain the existence of such molecules as \(H_2\), \(O_2\), and CO, since no separation distance exists for which the negative potential energy of attraction is greater in magnitude than the energy needed to create ions. Understanding precisely how such molecules are covalently bonded relies on a deeper understanding of quantum mechanics that goes beyond the coverage of this book, but we will qualitatively describe the mechanisms in the following section.
Covalent bonds can be understood using the simple example of \(\ce{H_2^{+}}\) molecule, which consists of one electron in the electric field of two protons. This system can be modeled by an electron in a double square well (Figure \(\PageIndex{2}\)). The electron is equally likely to be found in each well, so the wave function is either symmetric or antisymmetric about a point midway between the wells.
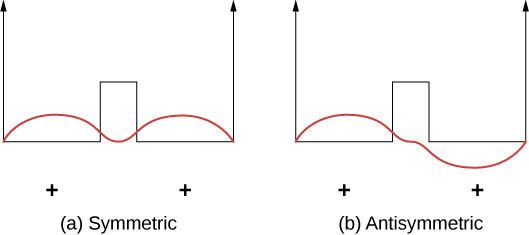
Now imagine that the two wells are separated by a large distance. In the ground state, the wave function exists in one of two possible states: either a single positive peak (a sine wave-like “hump”) in both wells (symmetric case), or a positive peak in one well and a negative peak in the other (antisymmetric case). These states have the same energy. However, when the wells are brought together, the symmetric wave function becomes the ground state and the antisymmetric state becomes the first excited state—in other words, the energy level of the electron is split. Notice, the space-symmetric state becomes the energetically favorable (lower energy) state.
The same analysis is appropriate for an electron bound to two hydrogen atoms. Here, the shapes of the ground-state wave functions have the form \(e^{-r/a_0}\) or \(e^{(-|x|/a_0)}\) in one dimension. The energetically favorable, space-symmetric state implies a high charge density midway between the protons where the electrons are likely to pull the positively charged protons together.
If a second electron is added to this system to form a \(H_2\) molecule, the wave function must describe both particles, including their spatial relationship and relative spins. This wave function must also respect the indistinguishability of electrons. (“If you’ve seen one electron, you’ve seen them all.”) In particular, switching or exchanging the electrons should not produce an observable effect, a property called exchange symmetry. Exchange symmetry can be symmetric, producing no change in the wave function, or antisymmetric, producing an overall change in the sign of the wave function—neither of which is observable.
As we discuss later, the total wave function of two electrons must be antisymmetric on exchange. For example, two electrons bound to a hydrogen molecule can be in a space-symmetric state with antiparallel spins (↑↓) or space-antisymmetric state with parallel spins (↑↑). The state with antiparallel spins is energetically favorable and therefore used in covalent bonding. If the protons are drawn too closely together, however, repulsion between the protons becomes important. (In other molecules, this effect is supplied by the exclusion principle.) As a result, \(H_2\) reaches an equilibrium separation of about 0.074 nm with a binding energy is 4.52 eV.
Visit this PBS Learning Media tutorial and interactive simulation to explore the attractive and repulsive forces that act on atomic particles and covalent bonding in a \(H_2\) molecule.
Quantum mechanics excludes many types of molecules. For example, the molecule \(H_3\) does not form, because if a third H atom approaches diatomic hydrogen, the wave function of the electron in this atom overlaps the electrons in the other two atoms. If all three electrons are in the ground states of their respective atoms, one pair of electrons shares all the same quantum numbers, which is forbidden by the exclusion principle. Instead, one of the electrons is forced into a higher energy state. No separation between three protons exists for which the total energy change of this process is negative—that is, where bonding occurs spontaneously. Similarly, \(He_2\) is not covalently bonded under normal conditions, because these atoms have no valence electrons to share. As the atoms are brought together, the wave functions of the core electrons overlap, and due to the exclusion principle, the electrons are forced into a higher energy state. No separation exists for which such a molecule is energetically favorable.
Bonding in Polyatomic Molecules
A polyatomic molecule is a molecule made of more than two atoms. Examples range from a simple water molecule to a complex protein molecule. The structures of these molecules can often be understood in terms of covalent bonding and hybridization. Hybridization is a change in the energy structure of an atom in which mixed states (states that can be written as a linear superposition of others) participate in bonding.
To illustrate hybridization, consider the bonding in a simple water molecule, \(H_2O\). The electron configuration of oxygen is \(1s^22s^22p^4\). The 1s and 2s electrons are in “closed shells” and do not participate in bonding. The remaining four electrons are the valence electrons. These electrons can fill six possible states (\(l = 1, m = 0, \pm 1\), plus spin up and down). The energies of these states are the same, so the oxygen atom can exploit any linear combination of these states in bonding with the hydrogen atoms. These linear combinations (which you learned about in the chapter on atomic structure) are called atomic orbitals, and they are denoted by \(p_x\), \(p_y\), and \(p_z\). The electron charge distributions for these orbitals are given in Figure \(\PageIndex{3}\).
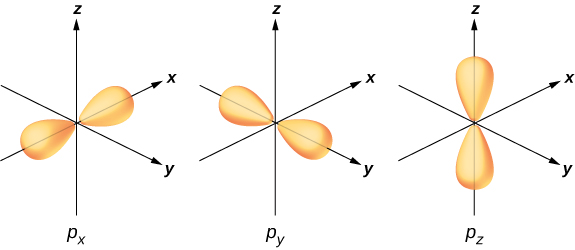
The transformation of the electron wave functions of oxygen to \(p_x, p_y\), and \(p_z\) orbitals in the presence of the hydrogen atoms is an example of hybridization. Two electrons are found in the \(p_z\) orbital with paired spins (↑↓). One electron is found in each of the \(p_x\) and \(p_y\) orbitals, with unpaired spins. The latter orbitals participate in bonding with the hydrogen atoms. Based on Figure \(\PageIndex{3}\), we expect the bonding angle for H—O—H to be 90°. However, if we include the effects of repulsion between atoms, the bond angle is 104.5°. The same arguments can be used to understand the tetrahedral shape of methane (\(CH_4\)) and other molecules.


