12.3: Magnetic Field due to a Thin Straight Wire
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain how the Biot-Savart law is used to determine the magnetic field due to a thin, straight wire.
- Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire.
- Sketch the magnetic field created from a thin, straight wire by using the second right-hand rule.
How much current is needed to produce a significant magnetic field, perhaps as strong as Earth’s field? Surveyors will tell you that overhead electric power lines create magnetic fields that interfere with their compass readings. Indeed, when Oersted discovered in 1820 that a current in a wire affected a compass needle, he was not dealing with extremely large currents. How does the shape of wires carrying current affect the shape of the magnetic field created? We noted in Chapter 28 that a current loop created a magnetic field similar to that of a bar magnet, but what about a straight wire? We can use the Biot-Savart law to answer all of these questions, including determining the magnetic field of a long straight wire.
Figure 12.3.1 shows a section of an infinitely long, straight wire that carries a current I. What is the magnetic field at a point P, located a distance R from the wire?
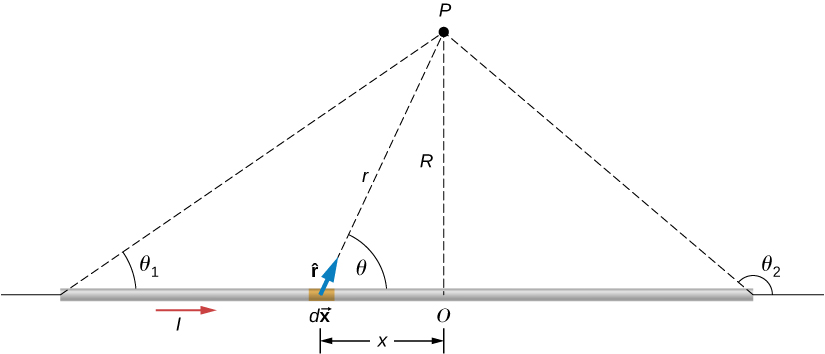
Let’s begin by considering the magnetic field due to the current element Id→x located at the position x. Using the right-hand rule 1 from the previous chapter, d→x׈r points out of the page for any element along the wire. At point P, therefore, the magnetic fields due to all current elements have the same direction. This means that we can calculate the net field there by evaluating the scalar sum of the contributions of the elements. With
|d→x׈r|=(dx)(1)sinθ
we have from the Biot-Savart law
B=μ04π∫wireIsinθdxr2.
The wire is symmetrical about point O, so we can set the limits of the integration from zero to infinity and double the answer, rather than integrate from negative infinity to positive infinity. Based on the picture and trigonometry, we can write expressions for r and sinθ in terms of x and R, namely:
r=√x2+R2
sinθ=R√x2+R2.
Substituting these expressions into Equation ???, the magnetic field integration becomes
B=μ0I2π∫∞0Rdx(x2+R2)3/2.
Evaluating the integral yields
B=μ0I2πR[x(x2+R2)1/2]∞0.
Substituting the limits gives us the solution
B=μ0I2πR.
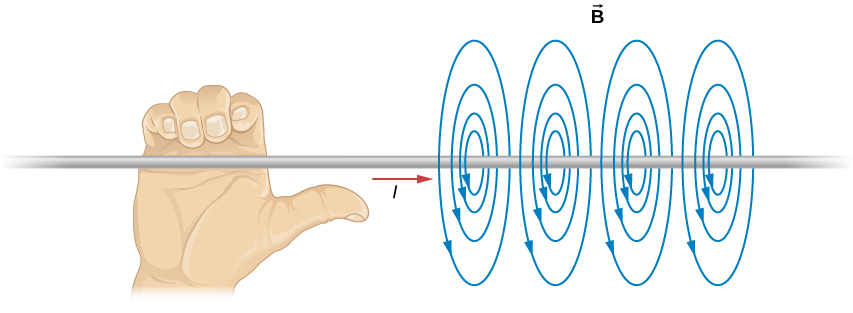
The magnetic field lines of the infinite wire are circular and centered at the wire (Figure 12.3.2), and they are identical in every plane perpendicular to the wire. Since the field decreases with distance from the wire, the spacing of the field lines must increase correspondingly with distance. The direction of this magnetic field may be found with a second form of the right-hand rule (Figure 12.3.2). If you hold the wire with your right hand so that your thumb points along the current, then your fingers wrap around the wire in the same sense as →B.
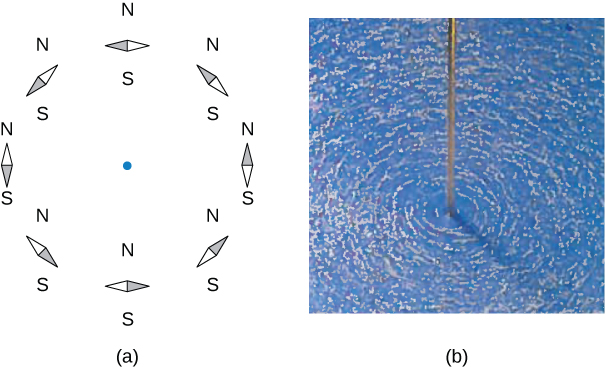
The direction of the field lines can be observed experimentally by placing several small compass needles on a circle near the wire, as illustrated in Figure 12.3.3a. When there is no current in the wire, the needles align with Earth’s magnetic field. However, when a large current is sent through the wire, the compass needles all point tangent to the circle. Iron filings sprinkled on a horizontal surface also delineate the field lines, as shown in Figure 12.3.3b.
Three wires sit at the corners of a square, all carrying currents of 2 amps into the page as shown in Figure 12.3.4. Calculate the magnitude of the magnetic field at the other corner of the square, point P, if the length of each side of the square is 1 cm.
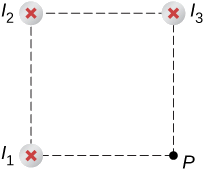
Strategy
The magnetic field due to each wire at the desired point is calculated. The diagonal distance is calculated using the Pythagorean theorem. Next, the direction of each magnetic field’s contribution is determined by drawing a circle centered at the point of the wire and out toward the desired point. The direction of the magnetic field contribution from that wire is tangential to the curve. Lastly, working with these vectors, the resultant is calculated.
Solution
Wires 1 and 3 both have the same magnitude of magnetic field contribution at point P:
B1=B3=μ0I2πR=(4π×10−7T⋅m/A)(2A)2π(0.01m)=4×10−5T.
Wire 2 has a longer distance and a magnetic field contribution at point P of:
B2=μ0I2πR=(4π×10−7T⋅m/A)(2A)2π(0.01414m)=3×10−5T.
The vectors for each of these magnetic field contributions are shown.
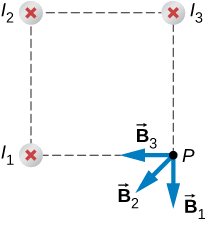
The magnetic field in the x-direction has contributions from wire 3 and the x-component of wire 2:
Bnetx=−4×10−5T−2.83×10−5Tcos(45o)=−6×10−5T.
The y-component is similarly the contributions from wire 1 and the y-component of wire 2:
Bnety=−4×10−5T−2.83×10−5Tsin(45o)=−6×10−5T.
Therefore, the net magnetic field is the resultant of these two components:
Bnet=√B2netx+Bnety=√(−6×10−5T)2+(−6×10−5T)2=8.48×10−5T.
Significance
The geometry in this problem results in the magnetic field contributions in the x- and y-directions having the same magnitude. This is not necessarily the case if the currents were different values or if the wires were located in different positions. Regardless of the numerical results, working on the components of the vectors will yield the resulting magnetic field at the point in need.
Using Example 12.3.1, keeping the currents the same in wires 1 and 3, what should the current be in wire 2 to counteract the magnetic fields from wires 1 and 3 so that there is no net magnetic field at point P?
Solution
4 amps flowing out of the page


