3.9: The First Law of Thermodynamics (Exercise)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
3.2 Thermodynamic Systems
1. Consider these scenarios and state whether work is done by the system on the environment (SE) or by the environment on the system (ES):
(a) opening a carbonated beverage;
(b) filling a flat tire;
(c) a sealed empty gas can expands on a hot day, bowing out the walls.
3.3 Work, Heat, and Internal Energy
2. Is it possible to determine whether a change in internal energy is caused by heat transferred, by work performed, or by a combination of the two?
3. When a liquid is vaporized, its change in internal energy is not equal to the heat added. Why?
4. Why does a bicycle pump feel warm as you inflate your tire?
5. Is it possible for the temperature of a system to remain constant when heat flows into or out of it? If so, give examples.
3.4 First Law of Thermodynamics
6. What does the first law of thermodynamics tell us about the energy of the universe?
7. Does adding heat to a system always increase its internal energy?
8. A great deal of effort, time, and money has been spent in the quest for a so-called perpetual-motion machine, which is defined as a hypothetical machine that operates or produces useful work indefinitely and/or a hypothetical machine that produces more work or energy than it consumes. Explain, in terms of the first law of thermodynamics, why or why not such a machine is likely to be constructed.
3.5 Thermodynamic Processes
9. When a gas expands isothermally, it does work. What is the source of energy needed to do this work?
10. If the pressure and volume of a system are given, is the temperature always uniquely determined?
11. It is unlikely that a process can be isothermal unless it is a very slow process. Explain why. Is the same true for isobaric and isochoric processes? Explain your answer.
3.6 Heat Capacities of an Ideal Gas
12. How can an object transfer heat if the object does not possess a discrete quantity of heat?
13. Most materials expand when heated. One notable exception is water between 0°C and 4°C, which actually decreases in volume with the increase in temperature. Which is greater for water in this temperature region, Cp or CV ?
14. Why are there two specific heats for gases Cp and CV, yet only one given for solid?
3.7 Adiabatic Processes for an Ideal Gas
15. Is it possible for γ to be smaller than unity?
16. Would you expect γ to be larger for a gas or a solid? Explain.
17. There is no change in the internal energy of an ideal gas undergoing an isothermal process since the internal energy depends only on the temperature. Is it therefore correct to say that an isothermal process is the same as an adiabatic process for an ideal gas? Explain your answer.
18. Does a gas do any work when it expands adiabatically? If so, what is the source of the energy needed to do this work?
Problems
3.2 Thermodynamic Systems
19. A gas follows pV=bp+cT on an isothermal curve, where p is the pressure, V is the volume, b is a constant, and c is a function of temperature. Show that a temperature scale under an isochoric process can be established with this gas and is identical to that of an ideal gas.
20. A mole of gas has isobaric expansion coefficient dV/dT=R/p and isochoric pressure-temperature coefficient dp/dT=p/T. Find the equation of state of the gas.
21. Find the equation of state of a solid that has an isobaric expansion coefficient dV/dT=2cT−bp and an isothermal pressure-volume coefficient dV/dp=−bT.
3.3 Work, Heat, and Internal Energy
22. A gas at a pressure of 2.00 atm undergoes a quasi-static isobaric expansion from 3.00 to 5.00 L. How much work is done by the gas?
23. It takes 500 J of work to compress quasi-statically 0.50 mol of an ideal gas to one-fifth its original volume. Calculate the temperature of the gas, assuming it remains constant during the compression.
24. It is found that, when a dilute gas expands quasi-statically from 0.50 to 4.0 L, it does 250 J of work. Assuming that the gas temperature remains constant at 300 K, how many moles of gas are present?
25. In a quasi-static isobaric expansion, 500 J of work are done by the gas. If the gas pressure is 0.80 atm, what is the fractional increase in the volume of the gas, assuming it was originally at 20.0 L?
26. When a gas undergoes a quasi-static isobaric change in volume from 10.0 to 2.0 L, 15 J of work from an external source are required. What is the pressure of the gas?
27. An ideal gas expands quasi-statically and isothermally from a state with pressure p and volume V to a state with volume 4V. Show that the work done by the gas in the expansion is pV(ln 4).
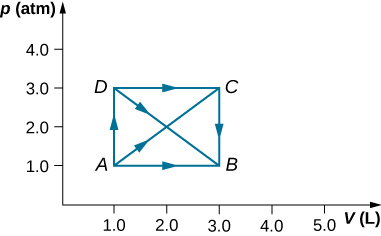
28. As shown below, calculate the work done by the gas in the quasi-static processes represented by the paths
(a) AB; (b) ADB; (c) ACB; and (d) ADCB
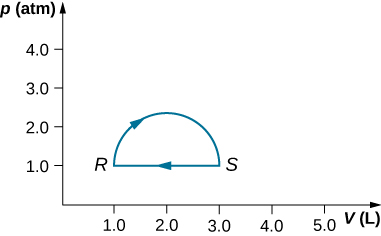
29. (a) Calculate the work done on the gas along the closed path shown below. The curved section between R and S is semicircular.
(b) If the process is carried out in the opposite direction, what is the work done on the gas?
30. An ideal gas expands quasi-statically to three times its original volume. Which process requires more work from the gas, an isothermal process or an isobaric one? Determine the ratio of the work done in these processes.
31. A dilute gas at a pressure of 2.0 atm and a volume of 4.0 L is taken through the following quasi-static steps: (a) an isobaric expansion to a volume of 10.0 L, (b) an isochoric change to a pressure of 0.50 atm, (c) an isobaric compression to a volume of 4.0 L, and (d) an isochoric change to a pressure of 2.0 atm. Show these steps on a pV diagram and determine from your graph the net work done by the gas.
32. What is the average mechanical energy of the atoms of an ideal monatomic gas at 300 K?
33. What is the internal energy of 6.00 mol of an ideal monatomic gas at 200°C?
34. Calculate the internal energy of 15 mg of helium at a temperature of 0°C.
35. Two monatomic ideal gases A and B are at the same temperature. If 1.0 g of gas A has the same internal energy as 0.10 g of gas B, what are
(a) the ratio of the number of moles of each gas and
(b) the ration of the atomic masses of the two gases?
36. The van der Waals coefficients for oxygen are a=0.138J⋅m3/mol2 and b=3.18×10−5m3/mol. Use these values to draw a van der Waals isotherm of oxygen at 100 K. On the same graph, draw isotherms of one mole of an ideal gas.
37. Find the work done in the quasi-static processes shown below. The states are given as (p, V) values for the points in the pV plane: 1 (3 atm, 4 L), 2 (3 atm, 6 L), 3 (5 atm, 4 L), 4 (2 atm, 6 L), 5 (4 atm, 2 L), 6 (5 atm, 5 L), and 7 (2 atm, 5 L).
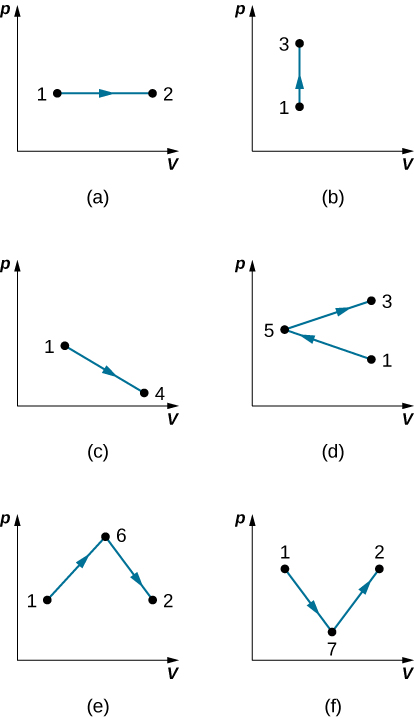
3.4 First Law of Thermodynamics
38. When a dilute gas expands quasi-statically from 0.50 to 4.0 L, it does 250 J of work. Assuming that the gas temperature remains constant at 300 K,
(a) what is the change in the internal energy of the gas?
(b) How much heat is absorbed by the gas in this process?
39. In an expansion, 500 J of work are done by the gas. If the internal energy of the gas increased by 80 J in the expansion, how much heat does the gas absorb?
40. An ideal gas expands quasi-statically and isothermally from a state with pressure p and volume V to a state with volume 4V. How much heat is added to the expanding gas?
41. As shown below, if the heat absorbed by the gas along AB is 400 J, determine the quantities of heat absorbed along
(a) ADB; (b) ACB; and (c) ADCB.

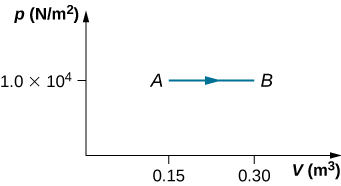
42. During the isobaric expansion from A to B represented below, 3,100 J of heat are added to the gas. What is the change in its internal energy?
43. (a) What is the change in internal energy for the process represented by the closed path shown below? (b) How much heat is exchanged? (c) If the path is traversed in the opposite direction, how much heat is exchanged?

44. When a gas expands along path AC shown below, it does 400 J of work and absorbs either 200 or 400 J of heat.
(a) Suppose you are told that along path ABC, the gas absorbs either 200 or 400 J of heat. Which of these values is correct?
(b) Give the correct answer from part (a), how much work is done by the gas along ABC?
(c) Along CD, the internal energy of the gas decreases by 50 J. How much heat is exchanged by the gas along this path?
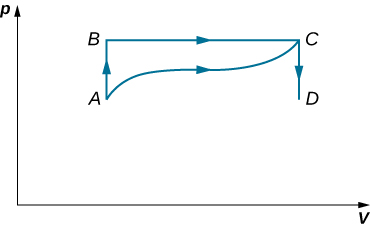
45. When a gas expands along AB (see below), it does 500 J of work and absorbs 250 J of heat. When the gas expands along AC, it does 400 J of work and absorbs 300 J of heat.
(a) How much heat does the gas exchange along BC?
(b) When the gas makes the transition from C to A along CDA, 800 J of work are done on it from C to D. How much heat does it exchange along CDA?
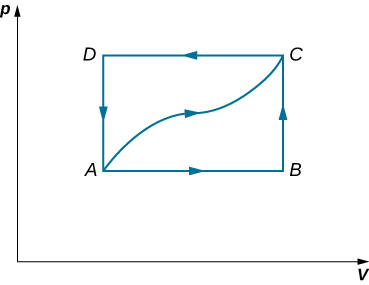
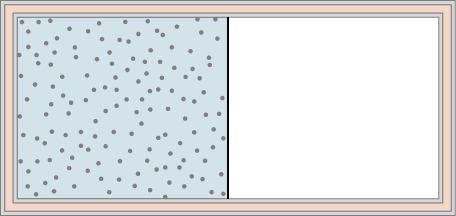
46. A dilute gas is stored in the left chamber of a container whose walls are perfectly insulating (see below), and the right chamber is evacuated. When the partition is removed, the gas expands and fills the entire container. Calculate the work done by the gas. Does the internal energy of the gas change in this process?
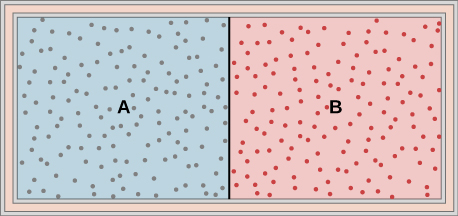
47. Ideal gases A and B are stored in the left and right chambers of an insulated container, as shown below. The partition is removed and the gases mix. Is any work done in this process? If the temperatures of A and B are initially equal, what happens to their common temperature after they are mixed?
48. An ideal monatomic gas at a pressure of .0×105N/m2 and a temperature of 300 K undergoes a quasi-static isobaric expansion from 2.0×103 to 4.0×103cm3.
(a) What is the work done by the gas?
(b) What is the temperature of the gas after the expansion?
(c) How many moles of gas are there?
(d) What is the change in internal energy of the gas?
(e) How much heat is added to the gas?
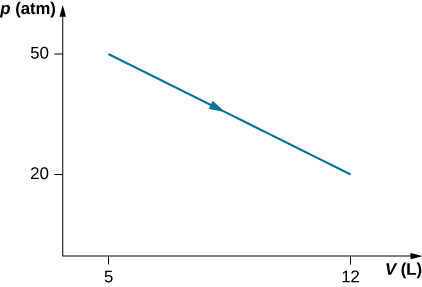
49. Consider the process for steam in a cylinder shown below. Suppose the change in the internal energy in this process is 30 kJ. Find the heat entering the system.
50. The state of 30 moles of steam in a cylinder is changed in a cyclic manner from a-b-c-a, where the pressure and volume of the states are: a (30 atm, 20 L), b (50 atm, 20 L), and c (50 atm, 45 L). Assume each change takes place along the line connecting the initial and final states in the pV plane.
(a) Display the cycle in the pV plane.
(b) Find the net work done by the steam in one cycle.
(c) Find the net amount of heat flow in the steam over the course of one cycle.
51. A monatomic ideal gas undergoes a quasi-static process that is described by the function p(V)=p1+3(V−V1), where the starting state is (p1,V1) and the final state (p2,V2). Assume the system consists of n moles of the gas in a container that can exchange heat with the environment and whose volume can change freely.
(a) Evaluate the work done by the gas during the change in the state.
(b) Find the change in internal energy of the gas.
(c) Find the heat input to the gas during the change.
(d) What are initial and final temperatures?
52. A metallic container of fixed volume of 2.5×10−3m3 immersed in a large tank of temperature 27°C contains two compartments separated by a freely movable wall. Initially, the wall is kept in place by a stopper so that there are 0.02 mol of the nitrogen gas on one side and 0.03 mol of the oxygen gas on the other side, each occupying half the volume. When the stopper is removed, the wall moves and comes to a final position. The movement of the wall is controlled so that the wall moves in infinitesimal quasi-static steps.
(a) Find the final volumes of the two sides assuming the ideal gas behavior for the two gases.
(b) How much work does each gas do on the other?
(c) What is the change in the internal energy of each gas?
(d) Find the amount of heat that enters or leaves each gas.
53. A gas in a cylindrical closed container is adiabatically and quasi-statically expanded from a state A (3 MPa, 2 L) to a stateB with volume of 6 L along the path 1.8pV=constant.
(a) Plot the path in the pV plane.
(b) Find the amount of work done by the gas and the change in the internal energy of the gas during the process.
3.5 Thermodynamic Processes
54. Two moles of a monatomic ideal gas at (5 MPa, 5 L) is expanded isothermally until the volume is doubled (step 1). Then it is cooled isochorically until the pressure is 1 MPa (step 2). The temperature drops in this process. The gas is now compressed isothermally until its volume is back to 5 L, but its pressure is now 2 MPa (step 3). Finally, the gas is heated isochorically to return to the initial state (step 4).
(a) Draw the four processes in the pV plane.
(b) Find the total work done by the gas.
55. Consider a transformation from point A to B in a two-step process. First, the pressure is lowered from 3 MPa at point A to a pressure of 1 MPa, while keeping the volume at 2 L by cooling the system. The state reached is labeled C. Then the system is heated at a constant pressure to reach a volume of 6 L in the state B.
(a) Find the amount of work done on the ACB path.
(b) Find the amount of heat exchanged by the system when it goes from A to B on the ACB path.
(c) Compare the change in the internal energy when the AB process occurs adiabatically with the AB change through the two-step process on the ACB path.
56. Consider a cylinder with a movable piston containing n moles of an ideal gas. The entire apparatus is immersed in a constant temperature bath of temperature T kelvin. The piston is then pushed slowly so that the pressure of the gas changes quasi-statically from p1p1 to p2p2 at constant temperature T. Find the work done by the gas in terms of n, R, T, p1, and p2.
57. An ideal gas expands isothermally along AB and does 700 J of work (see below).
(a) How much heat does the gas exchange along AB?
(b) The gas then expands adiabatically along BC and does 400 J of work. When the gas returns to A along CA, it exhausts 100 J of heat to its surroundings. How much work is done on the gas along this path?
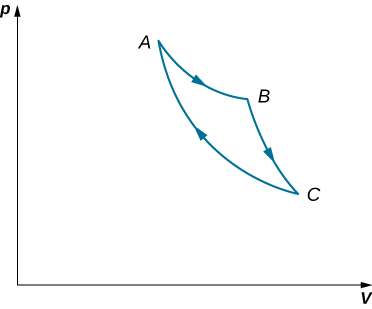
58. Consider the processes shown below for a monatomic gas.
(a) Find the work done in each of the processes AB, BC, AD, and DC.
(b) Find the internal energy change in processes AB and BC.
(c) Find the internal energy difference between states C and A.
(d) Find the total heat added in the ADC process.
(e) From the information given, can you find the heat added in process AD? Why or why not?
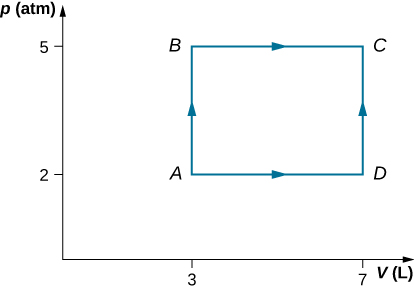
59. Two moles of helium gas are placed in a cylindrical container with a piston. The gas is at room temperature 25°C and under a pressure of 3.0×105Pa. When the pressure from the outside is decreased while keeping the temperature the same as the room temperature, the volume of the gas doubles.
(a) Find the work the external agent does on the gas in the process.
(b) Find the heat exchanged by the gas and indicate whether the gas takes in or gives up heat. Assume ideal gas behavior.
60. An amount of n moles of a monatomic ideal gas in a conducting container with a movable piston is placed in a large thermal heat bath at temperature T1 and the gas is allowed to come to equilibrium. After the equilibrium is reached, the pressure on the piston is lowered so that the gas expands at constant temperature. The process is continued quasi-statically until the final pressure is 4/3 of the initial pressure p1.
(a) Find the change in the internal energy of the gas.
(b) Find the work done by the gas.
(c) Find the heat exchanged by the gas, and indicate, whether the gas takes in or gives up heat.
3.6 Heat Capacities of an Ideal Gas
61. The temperature of an ideal monatomic gas rises by 8.0 K. What is the change in the internal energy of 1 mol of the gas at constant volume?
62. For a temperature increase of 10°C at constant volume, what is the heat absorbed by (a) 3.0 mol of a dilute monatomic gas; (b) 0.50 mol of a dilute diatomic gas; and (c) 15 mol of a dilute polyatomic gas?
63. If the gases of the preceding problem are initially at 300 K, what are their internal energies after they absorb the heat?
64. Consider 0.40 mol of dilute carbon dioxide at a pressure of 0.50 atm and a volume of 50 L. What is the internal energy of the gas?
65. When 400 J of heat are slowly added to 10 mol of an ideal monatomic gas, its temperature rises by 10°C. What is the work done on the gas?
66. One mole of a dilute diatomic gas occupying a volume of 10.00 L expands against a constant pressure of 2.000 atm when it is slowly heated. If the temperature of the gas rises by 10.00 K and 400.0 J of heat are added in the process, what is its final volume?
3.7 Adiabatic Processes for an Ideal Gas
67. A monatomic ideal gas undergoes a quasi-static adiabatic expansion in which its volume is doubled. How is the pressure of the gas changed?
68. An ideal gas has a pressure of 0.50 atm and a volume of 10 L. It is compressed adiabatically and quasi-statically until its pressure is 3.0 atm and its volume is 2.8 L. Is the gas monatomic, diatomic, or polyatomic?
69. Pressure and volume measurements of a dilute gas undergoing a quasi-static adiabatic expansion are shown below. Plot ln p vs. V and determine γγ for this gas from your graph.
| P (atm) | V(L) |
| 20.0 | 1.0 |
| 17.0 | 1.1 |
| 14.0 | 1.3 |
| 11.0 | 1.5 |
| 8.0 | 2.0 |
| 5.0 | 2.6 |
| 2.0 | 5.2 |
| 1.0 | 8.4 |
70. An ideal monatomic gas at 300 K expands adiabatically and reversibly to twice its volume. What is its final temperature?
71. An ideal diatomic gas at 80 K is slowly compressed adiabatically and reversibly to half its volume. What is its final temperature?
72. An ideal diatomic gas at 80 K is slowly compressed adiabatically to one-third its original volume. What is its final temperature?
73. Compare the charge in internal energy of an ideal gas for a quasi-static adiabatic expansion with that for a quasi-static isothermal expansion. What happens to the temperature of an ideal gas in an adiabatic expansion?
74. The temperature of n moles of an ideal gas changes from T1 to T2 in a quasi-static adiabatic transition. Show that the work done by the gas is given by W=nRγ−1(T1−T2).
75. A dilute gas expands quasi-statically to three times its initial volume. Is the final gas pressure greater for an isothermal or an adiabatic expansion? Does your answer depend on whether the gas is monatomic, diatomic, or polyatomic?
76. (a) An ideal gas expands adiabatically from a volume of 2.0×10−3m3 to 2.5×10−3m3. If the initial pressure and temperature were 5.0×105Pa and 300 K, respectively, what are the final pressure and temperature of the gas? Use γ=5/3 for the gas.
(b) In an isothermal process, an ideal gas expands from a volume of 2.0×10−3m3 to 2.5×10−3m3. If the initial pressure and temperature were .0×105Pa and 300 K, respectively, what are the final pressure and temperature of the gas?
77. On an adiabatic process of an ideal gas pressure, volume and temperature change such that pVγ is constant with γ=5/3 for monatomic gas such as helium and γ=7/5 for diatomic gas such as hydrogen at room temperature. Use numerical values to plot two isotherms of 1 mol of helium gas using ideal gas law and two adiabatic processes mediating between them. Use T1=500K,V1=1L, and T2=300K for your plot.
78. Two moles of a monatomic ideal gas such as helium is compressed adiabatically and reversibly from a state (3 atm, 5 L) to a state with pressure 4 atm. (a) Find the volume and temperature of the final state. (b) Find the temperature of the initial state of the gas. (c) Find the work done by the gas in the process. (d) Find the change in internal energy of the gas in the process.
Additional Problems
79. Consider the process shown below. During steps AB and BC, 3600 J and 2400 J of heat, respectively, are added to the system.
(a) Find the work done in each of the processes AB, BC, AD, and DC.
(b) Find the internal energy change in processes AB and BC.
(c) Find the internal energy difference between states C and A.
(d) Find the total heat added in the ADCprocess.
(e) From the information given, can you find the heat added in process AD? Why or why not?

80. A car tire contains 0.0380m3 of air at a pressure of 2.20×105Pa (about 32 psi). How much more internal energy does this gas have than the same volume has at zero gauge pressure (which is equivalent to normal atmospheric pressure)?
81. A helium-filled toy balloon has a gauge pressure of 0.200 atm and a volume of 10.0 L. How much greater is the internal energy of the helium in the balloon than it would be at zero gauge pressure?
82. Steam to drive an old-fashioned steam locomotive is supplied at a constant gauge pressure of 1.75×106N/m2 (about 250 psi) to a piston with a 0.200-m radius.
(a) By calculating pΔV, find the work done by the steam when the piston moves 0.800 m. Note that this is the net work output, since gauge pressure is used.
(b) Now find the amount of work by calculating the force exerted times the distance traveled. Is the answer the same as in part (a)?
83. A hand-driven tire pump has a piston with a 2.50-cm diameter and a maximum stroke of 30.0 cm.
(a) How much work do you do in one stroke if the average gauge pressure is 2.4×105N/m2 (about 35 psi)?
(b) What average force do you exert on the piston, neglecting friction and gravitational force?
84. Calculate the net work output of a heat engine following path ABCDA as shown below.

85. What is the net work output of a heat engine that follows path ABDA in the preceding problem with a straight line from B toD? Why is the work output less than for path ABCDA?
86. Five moles of a monatomic ideal gas in a cylinder at 27°C is expanded isothermally from a volume of 5 L to 10 L.
(a) What is the change in internal energy?
(b) How much work was done on the gas in the process? (c) How much heat was transferred to the gas?
87. Four moles of a monatomic ideal gas in a cylinder at 27°C is expanded at constant pressure equal to 1 atm until its volume doubles.
(a) What is the change in internal energy?
(b) How much work was done by the gas in the process?
(c) How much heat was transferred to the gas?
88. Helium gas is cooled from 20°C to 10°C by expanding from 40 atm to 1 atm. If there is 1.4 mol of helium,
(a) What is the final volume of helium?
(b) What is the change in internal energy?
89. In an adiabatic process, oxygen gas in a container is compressed along a path that can be described by the following pressure in atm as a function of volume V, with V0=1L:p=(3.0atm)(V/V0)−1.2. The initial and final volumes during the process were 2 L and 1.5 L, respectively. Find the amount of work done on the gas.
90. A cylinder containing three moles of a monatomic ideal gas is heated at a constant pressure of 2 atm. The temperature of the gas changes from 300 K to 350 K as a result of the expansion. Find work done
(a) on the gas; and
(b) by the gas.
91. A cylinder containing three moles of nitrogen gas is heated at a constant pressure of 2 atm. The temperature of the gas changes from 300 K to 350 K as a result of the expansion. Find work done
(a) on the gas, and
(b) by the gas by using van der Waals equation of state instead of ideal gas law.
92. Two moles of a monatomic ideal gas such as helium is compressed adiabatically and reversibly from a state (3 atm, 5 L) to a state with a pressure of 4 atm.
(a) Find the volume and temperature of the final state.
(b) Find the temperature of the initial state.
(c) Find work done by the gas in the process.
(d) Find the change in internal energy in the process. Assume CV=5R and Cp=CV+R for the diatomic ideal gas in the conditions given.
93. An insulated vessel contains 1.5 moles of argon at 2 atm. The gas initially occupies a volume of 5 L. As a result of the adiabatic expansion the pressure of the gas is reduced to 1 atm.
(a) Find the volume and temperature of the final state.
(b) Find the temperature of the gas in the initial state.
(c) Find the work done by the gas in the process.
(d) Find the change in the internal energy of the gas in the process.
Challenge Problems
94. One mole of an ideal monatomic gas occupies a volume of 1.0×10−2m3 at a pressure of 2.0×105N/m2.
(a) What is the temperature of the gas?
(b) The gas undergoes a quasi-static adiabatic compression until its volume is decreased to 5.0×10−3m3. What is the new gas temperature?
(c) How much work is done on the gas during the compression?
(d) What is the change in the internal energy of the gas?
95. One mole of an ideal gas is initially in a chamber of volume 1.0×10−2m3 and at a temperature of 27°C.
(a) How much heat is absorbed by the gas when it slowly expands isothermally to twice its initial volume?
(b) Suppose the gas is slowly transformed to the same final state by first decreasing the pressure at constant volume and then expanding it isobarically. What is the heat transferred for this case?
(c) Calculate the heat transferred when the gas is transformed quasi-statically to the same final state by expanding it isobarically, then decreasing its pressure at constant volume.
96. A bullet of mass 10 g is traveling horizontally at 200 m/s when it strikes and embeds in a pendulum bob of mass 2.0 kg.
(a) How much mechanical energy is dissipated in the collision?
(b) Assuming that Cv for the bob plus bullet is 3R, calculate the temperature increase of the system due to the collision. Take the molecular mass of the system to be 200 g/mol.
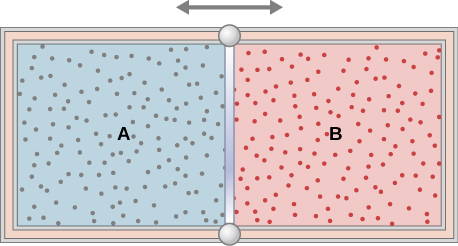
97. The insulated cylinder shown below is closed at both ends and contains an insulating piston that is free to move on frictionless bearings. The piston divides the chamber into two compartments containing gases A and B. Originally, each compartment has a volume of 5.0×10−2m3 and contains a monatomic ideal gas at a temperature of 0°C and a pressure of 1.0 atm.
(a) How many moles of gas are in each compartment?
(b) Heat Q is slowly added to A so that it expands and B is compressed until the pressure of both gases is 3.0 atm. Use the fact that the compression of B is adiabatic to determine the final volume of both gases.
(c) What are their final temperatures?
(d) What is the value of Q?
98. In a diesel engine, the fuel is ignited without a spark plug. Instead, air in a cylinder is compressed adiabatically to a temperature above the ignition temperature of the fuel; at the point of maximum compression, the fuel is injected into the cylinder. Suppose that air at 20°C is taken into the cylinder at a volume V1 and then compressed adiabatically and quasi-statically to a temperature of 600°C and a volume V2. If γ=1.4, what is the ratio V1/V2? (Note: In an operating diesel engine, the compression is not quasi-static.)


