11.6: Force and Torque on a Current Loop
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Evaluate the net force on a current loop in an external magnetic field
- Evaluate the net torque on a current loop in an external magnetic field
- Define the magnetic dipole moment of a current loop
Motors are the most common application of magnetic force on current-carrying wires. Motors contain loops of wire in a magnetic field. When current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft. Electrical energy is converted into mechanical work in the process. Once the loop’s surface area is aligned with the magnetic field, the direction of current is reversed, so there is a continual torque on the loop (Figure 11.6.1). This reversal of the current is done with commutators and brushes. The commutator is set to reverse the current flow at set points to keep continual motion in the motor. A basic commutator has three contact areas to avoid and dead spots where the loop would have zero instantaneous torque at that point. The brushes press against the commutator, creating electrical contact between parts of the commutator during the spinning motion.
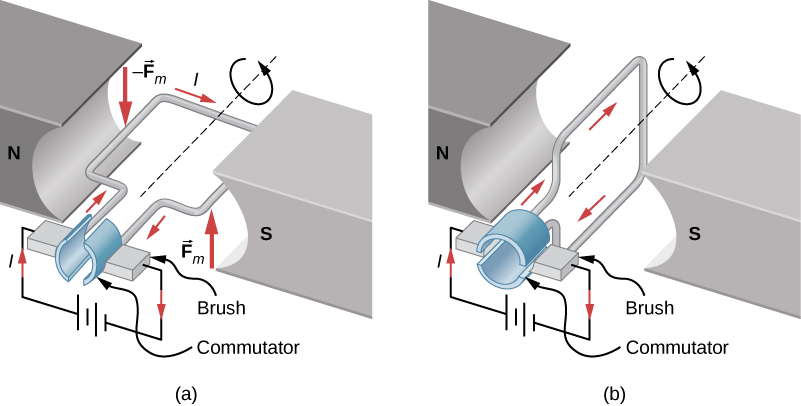
In a uniform magnetic field, a current-carrying loop of wire, such as a loop in a motor, experiences both forces and torques on the loop. Figure 11.6.1 shows a rectangular loop of wire that carries a current I and has sides of lengths a and b. The loop is in a uniform magnetic field: →B=Bˆj. The magnetic force on a straight current-carrying wire of length l is given by I→l×→B. To find the net force on the loop, we have to apply this equation to each of the four sides. The force on side 1 is
→F1=IaBsin(90o−θ)ˆi=IaBcosθˆi
where the direction has been determined with the RHR-1. The current in side 3 flows in the opposite direction to that of side 1, so
→F3=−IaBsin(90o+θ)ˆi=−IaBcosθˆi
The currents in sides 2 and 4 are perpendicular to →B and the forces on these sides are
→F2=IbBˆk
→F4=−IbBˆk.
We can now find the net force on the loop:
∑→Fnet=→F1+→F2+→F3+→F4=0.
Although this result (∑F=0) has been obtained for a rectangular loop, it is far more general and holds for current-carrying loops of arbitrary shapes; that is, there is no net force on a current loop in a uniform magnetic field.
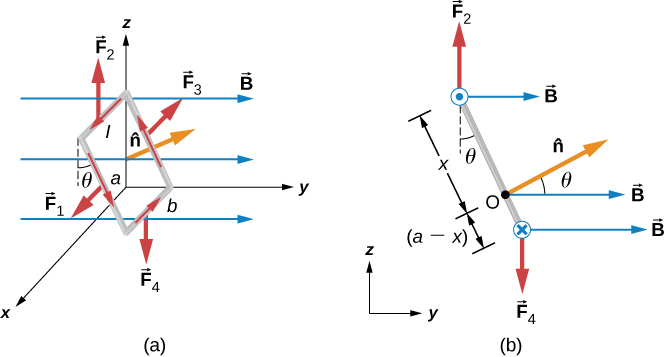
To find the net torque on the current loop shown in Figure 11.6.2a, we first consider F1 and F3. Since they have the same line of action and are equal and opposite, the sum of their torques about any axis is zero (see Fixed-Axis Rotation). Thus, if there is any torque on the loop, it must be furnished by F2 and F4. Let’s calculate the torques around the axis that passes through point O of Figure 11.6.2b (a side view of the coil) and is perpendicular to the plane of the page. The point O is a distance x from side 2 and a distance (a−x) from side 4 of the loop. The moment arms of F2 and F4 are xsinθ and (a−x) sinθ, respectively, so the net torque on the loop is
∑→τ=→τ1+→τ2+→τ3+→τ4=F2xsinθˆi−F4(a−x)sin(θ)ˆi
This simplifies to →τ=−IABsinθˆi
Notice that this torque is independent of x; it is therefore independent of where point O is located in the plane of the current loop. Consequently, the loop experiences the same torque from the magnetic field about any axis in the plane of the loop and parallel to the x-axis.
A closed-current loop is commonly referred to as a magnetic dipole and the term IA is known as its magnetic dipole moment μ. Actually, the magnetic dipole moment is a vector that is defined as
→μ=IAˆn
→μ=NIAˆn.
In terms of the magnetic dipole moment, the torque on a current loop due to a uniform magnetic field can be written simply as
→τ=→μ×→B.
This equation holds for a current loop in a two-dimensional plane of arbitrary shape.
Using a calculation analogous to that found in Capacitance for an electric dipole, the potential energy of a magnetic dipole is
U=−→μ⋅→B.
A circular current loop of radius 2.0 cm carries a current of 2.0 mA. (a) What is the magnitude of its magnetic dipole moment? (b) If the dipole is oriented at 30 degrees to a uniform magnetic field of magnitude 0.50 T, what is the magnitude of the torque it experiences and what is its potential energy?
Strategy
The dipole moment is defined by the current times the area of the loop. The area of the loop can be calculated from the area of the circle. The torque on the loop and potential energy are calculated from identifying the magnetic moment, magnetic field, and angle oriented in the field.
Solution
- The magnetic moment μ is calculated by the current times the area of the loop or πr2. μ=IA=(2.0×10−3A)(π(0.02m)2)=2.5×10−6A⋅m2
- The torque and potential energy are calculated by identifying the magnetic moment, magnetic field, and the angle between these two vectors. The calculations of these quantities are: τ=→μ×→B=μBsinθ=(2.5×10−6A⋅m2)(0.50T)sin(30o)=6.3×10−7N⋅mU=−→μ⋅→B=−μBcosθ=−(2.5×10−6A⋅m2)(0.50T)cos(30o)=−1.1×10−6J.
Significance
The concept of magnetic moment at the atomic level is discussed in the next chapter. The concept of aligning the magnetic moment with the magnetic field is the functionality of devices like magnetic motors, whereby switching the external magnetic field results in a constant spinning of the loop as it tries to align with the field to minimize its potential energy.
In what orientation would a magnetic dipole have to be to produce (a) a maximum torque in a magnetic field? (b) A maximum energy of the dipole?
a. aligned or anti-aligned; b. perpendicular


