16.3: Plane Electromagnetic Waves
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe how Maxwell’s equations predict the relative directions of the electric fields and magnetic fields, and the direction of propagation of plane electromagnetic waves
- Explain how Maxwell’s equations predict that the speed of propagation of electromagnetic waves in free space is exactly the speed of light
- Calculate the relative magnitude of the electric and magnetic fields in an electromagnetic plane wave
- Describe how electromagnetic waves are produced and detected
Mechanical waves travel through a medium such as a string, water, or air. Perhaps the most significant prediction of Maxwell’s equations is the existence of combined electric and magnetic (or electromagnetic) fields that propagate through space as electromagnetic waves. Because Maxwell’s equations hold in free space, the predicted electromagnetic waves, unlike mechanical waves, do not require a medium for their propagation.
A general treatment of the physics of electromagnetic waves is beyond the scope of this textbook. We can, however, investigate the special case of an electromagnetic wave that propagates through free space along the x-axis of a given coordinate system.
Electromagnetic Waves in One Direction
An electromagnetic wave consists of an electric field, defined as usual in terms of the force per charge on a stationary charge, and a magnetic field, defined in terms of the force per charge on a moving charge. The electromagnetic field is assumed to be a function of only the x-coordinate and time. The y-component of the electric field is then written as Ey(x,t), the z-component of the magnetic field as Bz(x,t), etc. Because we are assuming free space, there are no free charges or currents, so we can set Qin=0 and I=0 in Maxwell’s equations.
The transverse nature of electromagnetic waves
We examine first what Gauss’s law for electric fields implies about the relative directions of the electric field and the propagation direction in an electromagnetic wave. Assume the Gaussian surface to be the surface of a rectangular box whose cross-section is a square of side l and whose third side has length Δx, as shown in Figure 16.3.1. Because the electric field is a function only of x and t, the y-component of the electric field is the same on both the top (labeled Side 2) and bottom (labeled Side 1) of the box, so that these two contributions to the flux cancel. The corresponding argument also holds for the net flux from the z-component of the electric field through Sides 3 and 4. Any net flux through the surface therefore comes entirely from the x-component of the electric field. Because the electric field has no y- or z-dependence, Ex(x,t) is constant over the face of the box with area A and has a possibly different value Ex(x+Δx,t) that is constant over the opposite face of the box.
Applying Gauss’s law gives
Net flux=−Ex(x,t)A+Ex(x+Δx,t)A=Qinϵ0
where A=l×l is the area of the front and back faces of the rectangular surface. But the charge enclosed is Qin=0, so this component’s net flux is also zero, and Equation ??? implies Ex(x,t)=Ex(x+Δx,t) for any Δx. Therefore, if there is an x-component of the electric field, it cannot vary with x. A uniform field of that kind would merely be superposed artificially on the traveling wave, for example, by having a pair of parallel-charged plates. Such a component Ex(x,t) would not be part of an electromagnetic wave propagating along the x-axis; so Ex(x,t)=0 for this wave. Therefore, the only nonzero components of the electric field are Ey(x,t) and Ez(x,t) perpendicular to the direction of propagation of the wave.

A similar argument holds by substituting E for B and using Gauss’s law for magnetism instead of Gauss’s law for electric fields. This shows that the B field is also perpendicular to the direction of propagation of the wave. The electromagnetic wave is therefore a transverse wave, with its oscillating electric and magnetic fields perpendicular to its direction of propagation.
The speed of propagation of electromagnetic waves
We can next apply Maxwell’s equations to the description given in connection with Figure 16.2.3 in the previous section to obtain an equation for the E field from the changing B field, and for the B field from a changing E field. We then combine the two equations to show how the changing E and B fields propagate through space at a speed precisely equal to the speed of light.
First, we apply Faraday’s law over Side 3 of the Gaussian surface, using the path shown in Figure 16.3.2. Because Ex(x,t)=0, we have
∮→E⋅d→s=−Ey(x,t)l+Ey(x+Δx,t)l.
Assuming Δx is small and approximating Ey(x+Δx,t) by
Ey(x+Δx,t)=Ey(x,t)+∂Ey(x,t)∂xΔx,
we obtain
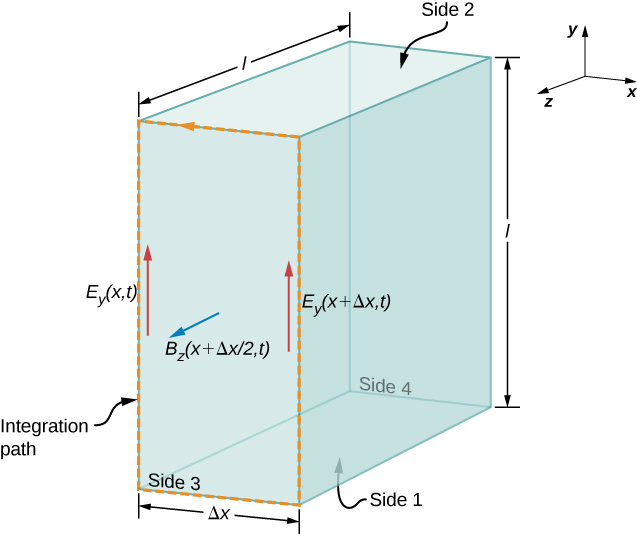
Because Δx is small, the magnetic flux through the face can be approximated by its value in the center of the area traversed, namely Bz(x+Δx2,t). The flux of the B field through Face 3 is then the B field times the area,
∮S→B⋅→ndA=Bz(x+Δx2,t)(lΔx).
From Faraday’s law,
∮→E⋅d→s=−ddt∫S→B⋅→ndA.
Therefore, from Equations ??? and ???,
∂Ey(x,t)∂x(lΔx)=−∂∂t[Bz(x+Δx2,t)](lΔx).
Canceling lΔx and taking the limit as Δx=0, we are left with
∂Ey(x,t)∂x=−∂Bz(x,t)∂t.
We could have applied Faraday’s law instead to the top surface (numbered 2) in Figure 16.3.2, to obtain the resulting equation
∂Bz(x,t)∂t=−∂Ey(x,t)∂x.
This is the equation describing the spatially dependent E field produced by the time-dependent B field.
Next we apply the Ampère-Maxwell law (with I=0) over the same two faces (Surface 3 and then Surface 2) of the rectangular box of Figure 16.3.2. Applying Equation 16.2.16,
∮→B⋅d→s=μ0ϵ0(d/dt)∫S→E⋅nda
to Surface 3, and then to Surface 2, yields the two equations
∂Ey(x,t)∂x=−ϵ0μ0∂Ez(x,t)∂t,
and
∂Bz(x,t)∂x=−ϵ0μ0∂Ey(x,t)∂t.
These equations describe the spatially dependent B field produced by the time-dependent E field.
We next combine the equations showing the changing B field producing an E field with the equation showing the changing E field producing a B field. Taking the derivative of Equation ??? with respect to x and using Equation ??? gives
∂2Ey∂x2=∂∂x(∂Ey∂x)=−∂∂x(∂Bz∂t)=−∂∂t(∂Bz∂x)=∂∂t(ϵ0μ0∂Ey∂t)
or
∂2Ey∂x2=ϵ0μ0∂2Ey∂t2
This is the form taken by the general wave equation for our plane wave. Because the equations describe a wave traveling at some as-yet-unspecified speed c, we can assume the field components are each functions of x – ct for the wave traveling in the +x-direction, that is,
Ey(x,t)=f(ξ)whereξ=x−ct.
It is left as a mathematical exercise to show, using the chain rule for differentiation, that Equations ??? and ??? imply
1=ϵ0μ0c2.
The speed of the electromagnetic wave in free space is therefore given in terms of the permeability and the permittivity of free space by
c=1√ϵ0μ0.
We could just as easily have assumed an electromagnetic wave with field components Ez(x,t) and By(x,t). The same type of analysis with Equation ??? and ??? would also show that the speed of an electromagnetic wave is c=1/√ϵ0μ0.
The physics of traveling electromagnetic fields was worked out by Maxwell in 1873. He showed in a more general way than our derivation that electromagnetic waves always travel in free space with a speed given by Equation ???. If we evaluate the speed c=1√ϵ0μ0, we find that
c=1√(8.85×10−12C2N⋅m2)(4π×10−7T⋅mA)=3.00×108m/s,
which is the speed of light. Imagine the excitement that Maxwell must have felt when he discovered this equation! He had found a fundamental connection between two seemingly unrelated phenomena: electromagnetic fields and light.
The wave equation was obtained by (1) finding the E field produced by the changing B field, (2) finding the B field produced by the changing E field, and combining the two results. Which of Maxwell’s equations was the basis of step (1) and which of step (2)?
- Answer (step 1)
-
Faraday’s law
- Answer (step 2)
-
the Ampère-Maxwell law
How the E and B Fields Are Related
So far, we have seen that the rates of change of different components of the E and B fields are related, that the electromagnetic wave is transverse, and that the wave propagates at speed c. We next show what Maxwell’s equations imply about the ratio of the E and B field magnitudes and the relative directions of the E and B fields.
We now consider solutions to Equation ??? in the form of plane waves for the electric field:
Ey(x,t)=E0cos(kx−ωt).
We have arbitrarily taken the wave to be traveling in the +x-direction and chosen its phase so that the maximum field strength occurs at the origin at time t=0. We are justified in considering only sines and cosines in this way, and generalizing the results, because Fourier’s theorem implies we can express any wave, including even square step functions, as a superposition of sines and cosines.
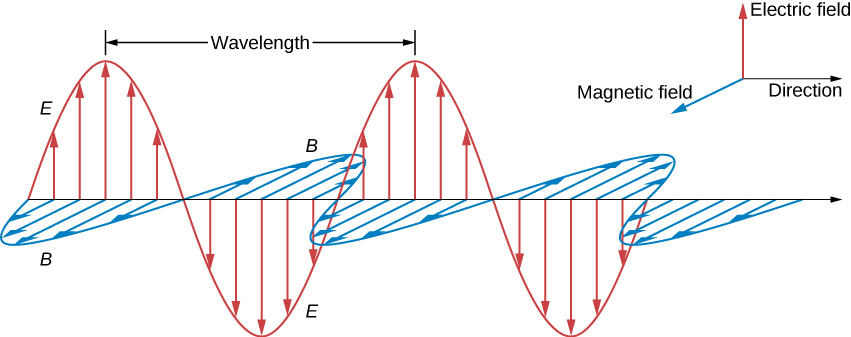
At any one specific point in space, the E field oscillates sinusoidally at angular frequency ω between +E0 and −E0 and similarly, the B field oscillates between +B0 and −B0. The amplitude of the wave is the maximum value of Ey(x,t). The period of oscillation T is the time required for a complete oscillation. The frequency f is the number of complete oscillations per unit of time, and is related to the angular frequency ω by ω=2πf. The wavelength λ is the distance covered by one complete cycle of the wave, and the wavenumber k is the number of wavelengths that fit into a distance of 2π in the units being used. These quantities are related in the same way as for a mechanical wave:
ω=2πf,f=1T,k=2πλ,andc=fλ=ω/k.
Given that the solution of Ey has the form shown in Equation ???, we need to determine the B field that accompanies it. From Equation ???, the magnetic field component Bz must obey
∂Bz∂t=−∂Ey∂x
∂Bz∂t=−∂∂xE0cos(kx−ωt)=kE0sin(kx−ωt).
Because the solution for the B-field pattern of the wave propagates in the +x-direction at the same speed c as the E-field pattern, it must be a function of k(x−ct)=kx−ωt. Thus, we conclude from Equation ??? that Bz is
Bz(x,t)=kωE0cos(kx−ωt)=1cE0cos(kx−ωt).
These results may be written as
Ey(x,t)=E0cos(kx−ωt)
Bz(x,t)=B0cos(kx−ωt)
EyBz=E0B0=c.
Therefore, the peaks of the E and B fields coincide, as do the troughs of the wave, and at each point, the E and B fields are in the same ratio equal to the speed of light c. The plane wave has the form shown in Figure 16.3.3.
What is the maximum strength of the B field in an electromagnetic wave that has a maximum E-field strength of 1000 V/m?
Strategy
To find the B-field strength, we rearrange Equation ??? to solve for B, yielding
B=Ec.
Solution We are given E, and c is the speed of light. Entering these into the expression for B yields
B=1000V/m3.00×108m/s=3.33×10−6T.
Significance
The B-field strength is less than a tenth of Earth’s admittedly weak magnetic field. This means that a relatively strong electric field of 1000 V/m is accompanied by a relatively weak magnetic field.
Changing electric fields create relatively weak magnetic fields. The combined electric and magnetic fields can be detected in electromagnetic waves, however, by taking advantage of the phenomenon of resonance, as Hertz did. A system with the same natural frequency as the electromagnetic wave can be made to oscillate. All radio and TV receivers use this principle to pick up and then amplify weak electromagnetic waves, while rejecting all others not at their resonant frequency.
What conclusions did our analysis of Maxwell’s equations lead to about these properties of a plane electromagnetic wave:
- the relative directions of wave propagation, of the E field, and of B field,
- the speed of travel of the wave and how the speed depends on frequency, and
- the relative magnitudes of the E and B fields.
- Answer a
-
The directions of wave propagation, of the E field, and of B field are all mutually perpendicular.
- Answer b
-
The speed of the electromagnetic wave is the speed of light c=1/√ϵ0μ0 independent of frequency.
- Answer c
-
The ratio of electric and magnetic field amplitudes is E/B=c.
Production and Detection of Electromagnetic Waves
A steady electric current produces a magnetic field that is constant in time and which does not propagate as a wave. Accelerating charges, however, produce electromagnetic waves. An electric charge oscillating up and down, or an alternating current or flow of charge in a conductor, emit radiation at the frequencies of their oscillations. The electromagnetic field of a dipole antenna is shown in Figure 16.3.4. The positive and negative charges on the two conductors are made to reverse at the desired frequency by the output of a transmitter as the power source. The continually changing current accelerates charge in the antenna, and this results in an oscillating electric field a distance away from the antenna. The changing electric fields produce changing magnetic fields that in turn produce changing electric fields, which thereby propagate as electromagnetic waves. The frequency of this radiation is the same as the frequency of the ac source that is accelerating the electrons in the antenna. The two conducting elements of the dipole antenna are commonly straight wires. The total length of the two wires is typically about one-half of the desired wavelength (hence, the alternative name half-wave antenna), because this allows standing waves to be set up and enhances the effectiveness of the radiation.
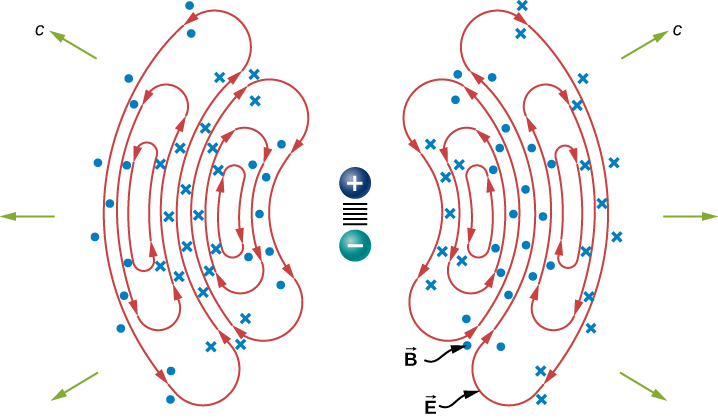
The electric field lines in one plane are shown. The magnetic field is perpendicular to this plane. This radiation field has cylindrical symmetry around the axis of the dipole. Field lines near the dipole are not shown. The pattern is not at all uniform in all directions. The strongest signal is in directions perpendicular to the axis of the antenna, which would be horizontal if the antenna is mounted vertically. There is zero intensity along the axis of the antenna. The fields detected far from the antenna are from the changing electric and magnetic fields inducing each other and traveling as electromagnetic waves. Far from the antenna, the wave fronts, or surfaces of equal phase for the electromagnetic wave, are almost spherical. Even farther from the antenna, the radiation propagates like electromagnetic plane waves.
The electromagnetic waves carry energy away from their source, similar to a sound wave carrying energy away from a standing wave on a guitar string. An antenna for receiving electromagnetic signals works in reverse. Incoming electromagnetic waves induce oscillating currents in the antenna, each at its own frequency. The radio receiver includes a tuner circuit, whose resonant frequency can be adjusted. The tuner responds strongly to tshe desired frequency but not others, allowing the user to tune to the desired broadcast. Electrical components amplify the signal formed by the moving electrons. The signal is then converted into an audio and/or video format.
Use this simulation to broadcast radio waves. Wiggle the transmitter electron manually or have it oscillate automatically. Display the field as a curve or vectors. The strip chart shows the electron positions at the transmitter and at the receiver.


