Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

2.A: Vectors (Answers)

Last updated

Nov 5, 2020
Save as PDF
- 2.9: Products of Vectors (Part 2)
- 2.E: Vectors (Exercises)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Check Your Understanding

2.1. a. not equal because they are orthogonal;

b. not equal because they have different magnitudes;

c. not equal because they have different magnitudes and directions;

d. not equal because they are antiparallel;

e. equal.

2.2. 16 m; $\vec{D}=−16m\hat{u}$

2.3. G = 28.2 cm, $θ_G=291°$

2.4. $\vec{D}=(−5.0\hat{i}−3.0\hat{j})cm$ ; the fly moved 5.0 cm to the left and 3.0 cm down from its landing site.

2.5. 5.83 cm, $211°$

2.6. $\vec{D}=(−20m)\hat{j}$

2.7. 35.1 m/s = 126.4 km/h

2.8. $\vec{G}=(10.25\hat{i}−26.22\hat{j})cm$

2.9. D = 55.7 N; direction $65.7°$ north of east

2.10. $\hat{v}=0.8\hat{i}+0.6\hat{j}, 36.87°$ north of east

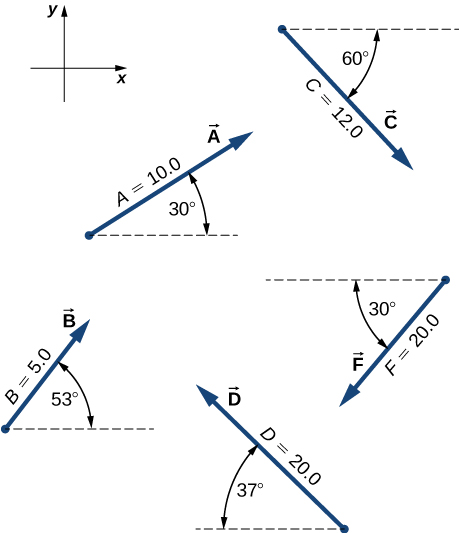
2.11. $\vec{A}⋅\vec{B}=−57.3, \vec{F}⋅\vec{C}=27.8$

2.13. $131.9°$

2.14. $W_1=1.5J, W_2=0.3J$

2.15. $\vec{A}×\vec{B}=−40.1\hat{k}$ or, equivalently, $∣\vec{A}×\vec{B}∣=40.1$ , and the direction is into the page; $\vec{C}×\vec{F}=+157.6\hat{k}$ or, equivalently, $∣\vec{C}×\vec{F}∣=157.6$ , and the direction is out of the page.

2.16. a. $−2\hat{k}$ ,

b. 2,

c. $153.4°$ ,

d. $135°$

Conceptual Questions

1. scalar

3. answers may vary

5. parallel, sum of magnitudes, antiparallel, zero

7. no, yes

9. zero, yes

11. no

13. equal, equal, the same

15. a unit vector of the x-axis

17. They are equal.

19. yes

21. a. $C=\vec{A}⋅\vec{B}$

b. $\vec{C}=\vec{A}·\vec{B}$ or $\vec{C}=\vec{A}−\vec{B}$

c. $\vec{C}=\vec{A}×\vec{B}$ ,

d. $\vec{C}=A\vec{B}$ ,

e. $\vec{C}+2\vec{A}=\vec{B}$ ,

f. $\vec{C}=\vec{A}×\vec{B}$ ,

g. left side is a scalar and right side is a vector,

h. $\vec{C}=2\vec{A}×\vec{B}$ ,

i. $\vec{C}=\vec{A}/B$ ,

j. $\vec{C}=\vec{A}/B$

23. They are orthogonal.

Problems

25. $\vec{h}=−49m\hat{u}$ , 49 m

27. 30.8 m, $35.7°$ west of north

29. 134 km, $80°$

31. 7.34 km, $63.5°$ south of east

33. 3.8 km east, 3.2 km north, 7.0 km

35. 14.3 km, $65°$

37. a. $\vec{A}=+8.66\hat{i}+5.00\hat{j}$ ,

b. $\vec{B}=+3.01\hat{i}+3.99\hat{j}$ ,

c. $\vec{C}=+6.00\hat{i}−10.39\hat{j}$ ,

d. $\vec{D⃗}=−15.97\hat{i}+12.04\hat{j}$ ,

f. $\vec{F}=−17.32\hat{i}−10.00\hat{j}$

39. a. 1.94 km, 7.24 km;

b. proof

41. 3.8 km east, 3.2 km north, 2.0 km, \(\vec{D}=(3.8\hat{i}+3.2\hat{j})km

43. $P_1(2.165m,1.250m), P_2(−1.900m,3.290m), 5.27 m$

45. 8.60 m, $A(2\sqrt{5}m,0.647π), B(3\sqrt{2}m,0.75π)$

47. a. $\vec{A}+\vec{B}=−4\hat{i}−6\hat{j}$ , $|\vec{A}+\vec{B}∣=7.211,θ=236.3°$ ;

b. $\vec{A}−\vec{B}=-2\hat{i}+2\hat{j}, ∣\vec{A}−\vec{B}∣=2\sqrt{2},θ=135°$

49. a. $\vec{C}=(5.0\hat{i}−1.0\hat{j}−3.0\hat{k})m,C=5.92m$ ;

b. $\vec{D}=(4.0\hat{i}−11.0\hat{j}+15.0\hat{k})m,D=19.03m$ .

51. $\vec{D}=(3.3\hat{i}−6.6\hat{j})km, \hat{i} is to the east, 7.34 km, −63.5°$

53. a. $\vec{R}=−1.35\hat{i}−22.04\hat{j}$ ,

b. $\vec{R}=−17.98\hat{i}+0.89\hat{j}$

55. $\vec{D}=(200\hat{i}+300\hat{j})yd$ , D = 360.5 yd, $56.3°$ north of east; The numerical answers would stay the same but the physical unit would be meters. The physical meaning and distances would be about the same because 1 yd is comparable with 1 m.

57. $\vec{R}=−3\hat{i}−16\hat{j}$

59. $\vec{E⃗}=E\hat{E}, E_x=+178.9V/m, E_y=−357.8V/m, E_z=0.0V/m, θ_E=−tan^{−1}(2)$

61. a. $\vec{R}_B=(12.278\hat{i}+7.089\hat{j}+2.500\hat{k})km, \(\vec{R}_D=(−0.262\hat{i}+3.000\hat{k})km$ ;

b. $∣\vec{R}_B−\vec{R}_D∣=14.414km$ |R→B−R→D|=14.414km

63. a. 8.66,

b. 10.39,

c. 0.866,

d. 17.32

65. $θ_i=64.12°,θ_j=150.79°,θ_k=77.39°$

67. a. $−119.98\hat{k}$

b. $0\hat{k}$ ,

c. $+93.69\hat{k}$ ,

d. $−240.0\hat{k}$ ,

e. $+3.993\hat{k}$ ,

f. $−3.009\hat{k}$ ,

g. $+14.99\hat{k}$ ,

h. 0

69. a. 0,

b. 173,194,

c. +199,993 $\hat{k}$

Additional Problems

71. a. 18.4 km and 26.2 km,

b. 31.5 km and 5.56 km

73. a. $(r,φ+π/2)$ ,

b. $(2r,φ+2π)($ ,

c. $(3r,−φ)$

75. $d_{PM}=33.12nmi=61.34km,d_{NP}=35.47nmi=65.69km$

77. proof

79. a. 10.00 m,

b. $5πm$ ,

c. 0

81. 22.2 km/h, $35.8°$ . south of west

83. 240.2 m, $2.2°$ south of west

85. $\vec{B}=−4.0\hat{i}+3.0\hat{j}$ or $\vec{B}=4.0\hat{i}−3.0\hat{j}$

87. proof

Challenge Problems

89. $G_{⊥}=2375\sqrt{17}≈9792$

91. proof

Check Your Understanding

Conceptual Questions

Problems

Additional Problems

Challenge Problems

Support Center

How can we help?