2.9: Microscopes and Telescopes
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain the physics behind the operation of microscopes and telescopes
- Describe the image created by these instruments and calculate their magnifications
Microscopes and telescopes are major instruments that have contributed hugely to our current understanding of the micro- and macroscopic worlds. The invention of these devices led to numerous discoveries in disciplines such as physics, astronomy, and biology, to name a few. In this section, we explain the basic physics that make these instruments work.
Microscopes
Although the eye is marvelous in its ability to see objects large and small, it obviously is limited in the smallest details it can detect. The desire to see beyond what is possible with the naked eye led to the use of optical instruments. We have seen that a simple convex lens can create a magnified image, but it is hard to get large magnification with such a lens. A magnification greater than 5× is difficult without distorting the image. To get higher magnification, we can combine the simple magnifying glass with one or more additional lenses. In this section, we examine microscopes that enlarge the details that we cannot see with the naked eye.
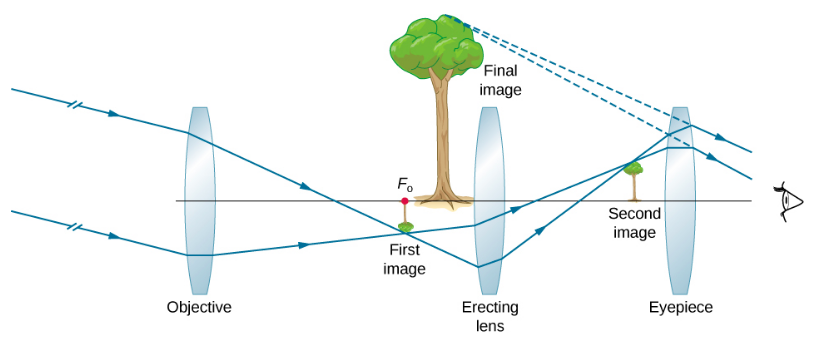
Microscopes were first developed in the early 1600s by eyeglass makers in The Netherlands and Denmark. The simplest compound microscope is constructed from two convex lenses (Figure 2.9.1). The objective lens is a convex lens of short focal length (i.e., high power) with typical magnification from 5× to 100×. The eyepiece, also referred to as the ocular, is a convex lens of longer focal length.
The purpose of a microscope is to create magnified images of small objects, and both lenses contribute to the final magnification. Also, the final enlarged image is produced sufficiently far from the observer to be easily viewed, since the eye cannot focus on objects or images that are too close (i.e., closer than the near point of the eye).
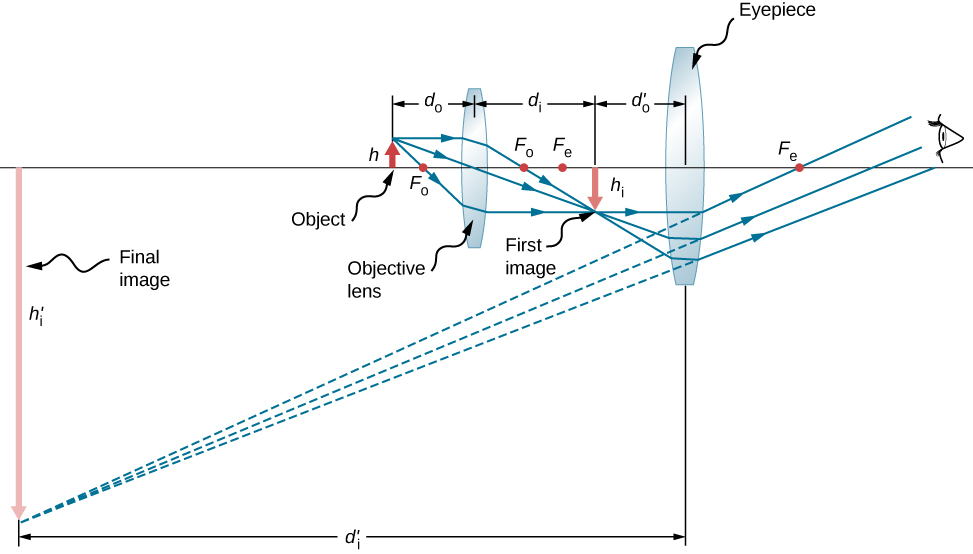
To see how the microscope in Figure 2.9.1 forms an image, consider its two lenses in succession. The object is just beyond the focal length fobj of the objective lens, producing a real, inverted image that is larger than the object. This first image serves as the object for the second lens, or eyepiece. The eyepiece is positioned so that the first image is within its focal length feye, so that it can further magnify the image. In a sense, it acts as a magnifying glass that magnifies the intermediate image produced by the objective. The image produced by the eyepiece is a magnified virtual image. The final image remains inverted but is farther from the observer than the object, making it easy to view.
The eye views the virtual image created by the eyepiece, which serves as the object for the lens in the eye. The virtual image formed by the eyepiece is well outside the focal length of the eye, so the eye forms a real image on the retina.
The magnification of the microscope is the product of the linear magnification mobj by the objective and the angular magnification Meye by the eyepiece. These are given by
mobj=−dobjidobjo≈−dobjifobj⏟linear magnification by objective Meye=1+25cmfeye⏟angular magnification by eyepiece
Here, fobj and feye are the focal lengths of the objective and the eyepiece, respectively. We assume that the final image is formed at the near point of the eye, providing the largest magnification. Note that the angular magnification of the eyepiece is the same as obtained earlier for the simple magnifying glass. This should not be surprising, because the eyepiece is essentially a magnifying glass, and the same physics applies here. The net magnification Mnet of the compound microscope is the product of the linear magnification of the objective and the angular magnification of the eyepiece:
Mnet=mobjMeye=−dobji(feye+25cm)fobjfeye.
Calculate the magnification of an object placed 6.20 mm from a compound microscope that has a 6.00 mm-focal length objective and a 50.0 mm-focal length eyepiece. The objective and eyepiece are separated by 23.0 cm.
Strategy
This situation is similar to that shown in Figure 2.9.1. To find the overall magnification, we must know the linear magnification of the objective and the angular magnification of the eyepiece. We can use Equation ???, but we need to use the thin-lens equation to find the image distance dobji of the objective.
Solution
Solving the thin-lens equation for dobji gives
dobji=(1fobj−1dobjo)−1=(16.00mm−16.20mm)−1=186mm=18.6cm
Inserting this result into Equation ??? along with the known values
- fobj=6.00mm=0.600cm
- feye=50.0mm=5.00cm
gives
Mnet=−dobji(feye+25cm)fobjfeye=−(18.6cm)(5.00cm+25cm)(0.600cm)(5.00cm)=−186
Significance
Both the objective and the eyepiece contribute to the overall magnification, which is large and negative, consistent with Figure 2.9.1, where the image is seen to be large and inverted. In this case, the image is virtual and inverted, which cannot happen for a single element.
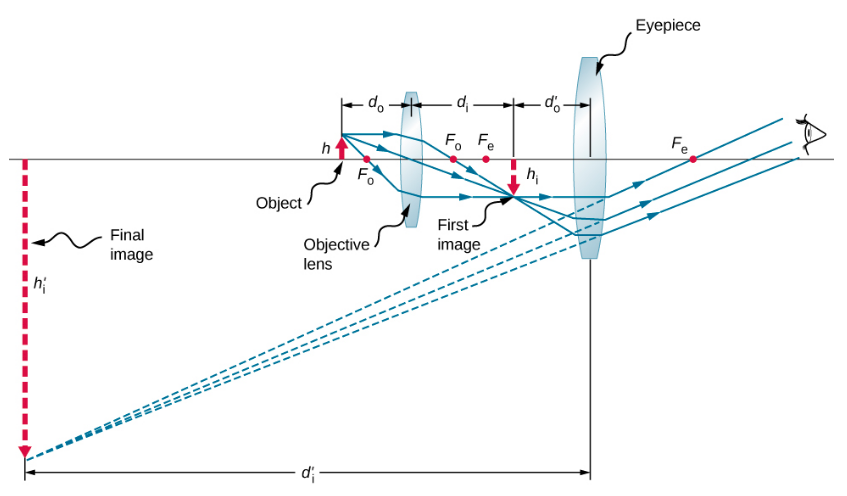
We now calculate the magnifying power of a microscope when the image is at infinity, as shown in Figure 2.9.2, because this makes for the most relaxed viewing. The magnifying power of the microscope is the product of linear magnification mobj of the objective and the angular magnification Meye of the eyepiece. We know that
mobj=−dobjidobjo
and from the thin-lens equation we obtain
mobj=−dobjidobjo=1−dobjifobj=fobj−dobjifobj.
If the final image is at infinity, then the image created by the objective must be located at the focal point of the eyepiece. This may be seen by considering the thin-lens equation with di=∞ or by recalling that rays that pass through the focal point exit the lens parallel to each other, which is equivalent to focusing at infinity. For many microscopes, the distance between the image-side focal point of the objective and the object-side focal point of the eyepiece is standardized at L = 16 cm. This distance is called the tube length of the microscope. From Figure 2.9.2, we see that
L=fobj−dobji.
Inserting this into Equation ??? gives
mobj=Lfobj=16cmfobj.
We now need to calculate the angular magnification of the eyepiece with the image at infinity. To do so, we take the ratio of the angle θimage subtended by the image to the angle θobject subtended by the object at the near point of the eye (this is the closest that the unaided eye can view the object, and thus this is the position where the object will form the largest image on the retina of the unaided eye). Using Figure 2.9.2 and working in the small-angle approximation, we have
θimage≈hobjifeye
and
θobject≈hobji25cm
where hobji is the height of the image formed by the objective, which is the object of the eyepiece. Thus, the angular magnification of the eyepiece is
Meye =θimage θobject =hobj ifeye 25cmhobj i=25cmfeye .
The net magnifying power of the compound microscope with the image at infinity is therefore
Mnet=mobjMeye=−(16cm)(25cm)fobjfeye.
The focal distances must be in centimeters. The minus sign indicates that the final image is inverted. Note that the only variables in the equation are the focal distances of the eyepiece and the objective, which makes this equation particularly useful.
Telescopes
Telescopes are meant for viewing distant objects and produce an image that is larger than the image produced in the unaided eye. Telescopes gather far more light than the eye, allowing dim objects to be observed with greater magnification and better resolution. Telescopes were invented around 1600, and Galileo was the first to use them to study the heavens, with monumental consequences. He observed the moons of Jupiter, the craters and mountains on the moon, the details of sunspots, and the fact that the Milky Way is composed of a vast number of individual stars.
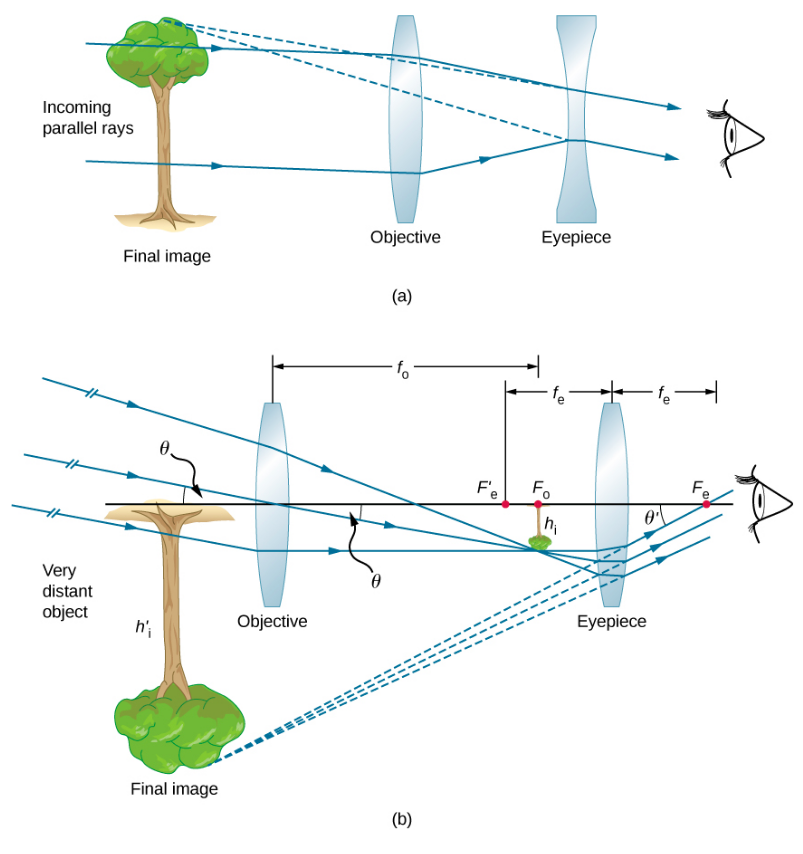
Figure 2.9.3a shows a refracting telescope made of two lenses. The first lens, called the objective, forms a real image within the focal length of the second lens, which is called the eyepiece. The image of the objective lens serves as the object for the eyepiece, which forms a magnified virtual image that is observed by the eye. This design is what Galileo used to observe the heavens.
Although the arrangement of the lenses in a refracting telescope looks similar to that in a microscope, there are important differences. In a telescope, the real object is far away and the intermediate image is smaller than the object. In a microscope, the real object is very close and the intermediate image is larger than the object. In both the telescope and the microscope, the eyepiece magnifies the intermediate image; in the telescope, however, this is the only magnification.
The most common two-lens telescope is shown in Figure 2.9.3b. The object is so far from the telescope that it is essentially at infinity compared with the focal lengths of the lenses dobjo≈∞, so the incoming rays are essentially parallel and focus on the focal plane. Thus, the first image is produced at
dobji=fobj
as shown in the figure, and is not large compared with what you might see by looking directly at the object. However, the eyepiece of the telescope eyepiece (like the microscope eyepiece) allows you to get nearer than your near point to this first image and so magnifies it (because you are near to it, it subtends a larger angle from your eye and so forms a larger image on your retina). As for a simple magnifier, the angular magnification of a telescope is the ratio of the angle subtended by the image (θimage in 2.9.3b) to the angle subtended by the real object (θobject in 2.9.3b):
M=θimageθobject.
To obtain an expression for the magnification that involves only the lens parameters, note that the focal plane of the objective lens lies very close to the focal plan of the eyepiece. If we assume that these planes are superposed, we have the situation shown in Figure 2.9.4.
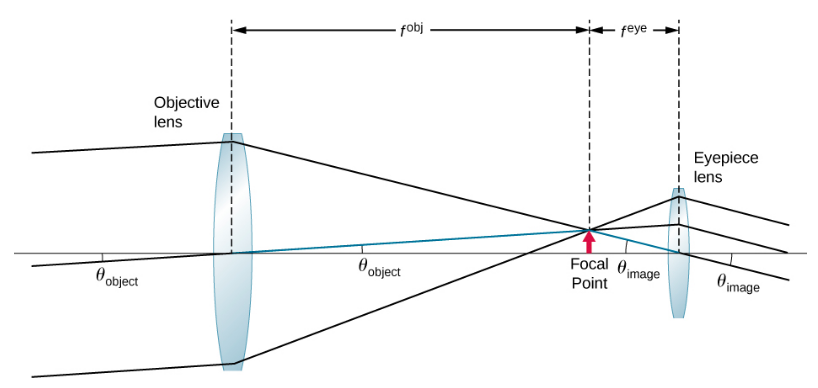
We further assume that the angles θobject and θimage are small, so that the small-angel approximation holds (tanθ≈θ). If the image formed at the focal plane has height h then
θobject ≈tanθobject =hfobj θimage ≈tanθimage =−hfeye
where the minus sign is introduced because the height is negative if we measure both angles in the counterclockwise direction. Inserting these expressions into Equation ??? gives
M=−hifeyefobjhi=−fobjfeye.
Thus, to obtain the greatest angular magnification, it is best to have an objective with a long focal length and an eyepiece with a short focal length. The greater the angular magnification M, the larger an object will appear when viewed through a telescope, making more details visible. Limits to observable details are imposed by many factors, including lens quality and atmospheric disturbance. Typical eyepieces have focal lengths of 2.5 cm or 1.25 cm. If the objective of the telescope has a focal length of 1 meter, then these eyepieces result in magnifications of 40× and 80×, respectively. Thus, the angular magnifications make the image appear 40 times or 80 times closer than the real object.
The minus sign in the magnification indicates the image is inverted, which is unimportant for observing the stars but is a real problem for other applications, such as telescopes on ships or telescopic gun sights. If an upright image is needed, Galileo’s arrangement in 2.9.3a can be used. But a more common arrangement is to use a third convex lens as an eyepiece, increasing the distance between the first two and inverting the image once again, as seen in Figure 2.9.5.
The largest refracting telescope in the world is the 40-inch diameter Yerkes telescope located at Lake Geneva, Wisconsin (Figure 2.9.6), and operated by the University of Chicago.
It is very difficult and expensive to build large refracting telescopes. You need large defect-free lenses, which in itself is a technically demanding task. A refracting telescope basically looks like a tube with a support structure to rotate it in different directions. A refracting telescope suffers from several problems. The aberration of lenses causes the image to be blurred. Also, as the lenses become thicker for larger lenses, more light is absorbed, making faint stars more difficult to observe. Large lenses are also very heavy and deform under their own weight. Some of these problems with refracting telescopes are addressed by avoiding refraction for collecting light and instead using a curved mirror in its place, as devised by Isaac Newton. These telescopes are called reflecting telescopes.

Reflecting Telescopes
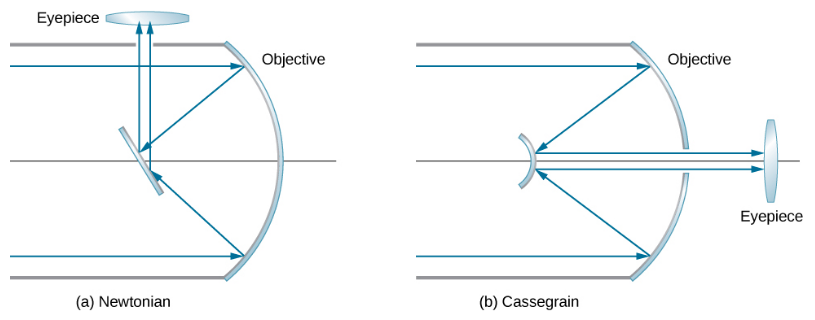
Isaac Newton designed the first reflecting telescope around 1670 to solve the problem of chromatic aberration that happens in all refracting telescopes. In chromatic aberration, light of different colors refracts by slightly different amounts in the lens. As a result, a rainbow appears around the image and the image appears blurred. In the reflecting telescope, light rays from a distant source fall upon the surface of a concave mirror fixed at the bottom end of the tube. The use of a mirror instead of a lens eliminates chromatic aberration. The concave mirror focuses the rays on its focal plane. The design problem is how to observe the focused image. Newton used a design in which the focused light from the concave mirror was reflected to one side of the tube into an eyepiece (Figure 2.9.7a). This arrangement is common in many amateur telescopes and is called the Newtonian design.
Some telescopes reflect the light back toward the middle of the concave mirror using a convex mirror. In this arrangement, the light-gathering concave mirror has a hole in the middle (2.9.7b). The light then is incident on an eyepiece lens. This arrangement of the objective and eyepiece is called the Cassegrain design. Most big telescopes, including the Hubble space telescope, are of this design. Other arrangements are also possible. In some telescopes, a light detector is placed right at the spot where light is focused by the curved mirror.
Most astronomical research telescopes are now of the reflecting type. One of the earliest large telescopes of this kind is the Hale 200-inch (or 5-meter) telescope built on Mount Palomar in southern California, which has a 200 inch-diameter mirror. One of the largest telescopes in the world is the 10-meter Keck telescope at the Keck Observatory on the summit of the dormant Mauna Kea volcano in Hawaii. The Keck Observatory operates two 10-meter telescopes. Each is not a single mirror, but is instead made up of 36 hexagonal mirrors. Furthermore, the two telescopes on the Keck can work together, which increases their power to an effective 85-meter mirror. The Hubble telescope (Figure 2.9.8) is another large reflecting telescope with a 2.4 meter-diameter primary mirror. The Hubble was put into orbit around Earth in 1990.

The angular magnification M of a reflecting telescope is also given by Equation ???. For a spherical mirror, the focal length is half the radius of curvature, so making a large objective mirror not only helps the telescope collect more light, but also increases the magnification of the image.


