3.5: Interference in Thin Films
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the phase changes that occur upon reflection
- Describe fringes established by reflected rays of a common source
- Explain the appearance of colors in thin films
The bright colors seen in an oil slick floating on water or in a sunlit soap bubble are caused by interference. The brightest colors are those that interfere constructively. This interference is between light reflected from different surfaces of a thin film; thus, the effect is known as thin-film interference.
As we noted before, interference effects are most prominent when light interacts with something having a size similar to its wavelength. A thin film is one having a thickness t smaller than a few times the wavelength of light, λ. Since color is associated indirectly with λ and because all interference depends in some way on the ratio of λ to the size of the object involved, we should expect to see different colors for different thicknesses of a film, as in Figure \PageIndex{1}.

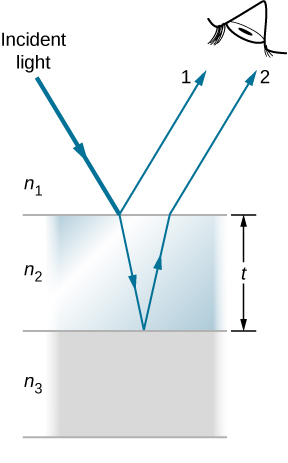
What causes thin-film interference? Figure \PageIndex{2} shows how light reflected from the top and bottom surfaces of a film can interfere. Incident light is only partially reflected from the top surface of the film (ray 1). The remainder enters the film and is itself partially reflected from the bottom surface. Part of the light reflected from the bottom surface can emerge from the top of the film (ray 2) and interfere with light reflected from the top (ray 1). The ray that enters the film travels a greater distance, so it may be in or out of phase with the ray reflected from the top. However, consider for a moment, again, the bubbles in Figure \PageIndex{1}. The bubbles are darkest where they are thinnest. Furthermore, if you observe a soap bubble carefully, you will note it gets dark at the point where it breaks. For very thin films, the difference in path lengths of rays 1 and 2 in Figure \PageIndex{2} is negligible, so why should they interfere destructively and not constructively? The answer is that a phase change can occur upon reflection, as discussed next.
Changes in Phase due to Reflection
We saw earlier (Waves) that reflection of mechanical waves can involve a 180° phase change. For example, a traveling wave on a string is inverted (i.e., a 180° phase change) upon reflection at a boundary to which a heavier string is tied. However, if the second string is lighter (or more precisely, of a lower linear density), no inversion occurs. Light waves produce the same effect, but the deciding parameter for light is the index of refraction. Light waves undergo a 180° or \pi radians phase change upon reflection at an interface beyond which is a medium of higher index of refraction. No phase change takes place when reflecting from a medium of lower refractive index (Figure \PageIndex{3}). Because of the periodic nature of waves, this phase change or inversion is equivalent to ±λ/2 in distance travelled, or path length. Both the path length and refractive indices are important factors in thin-film interference.
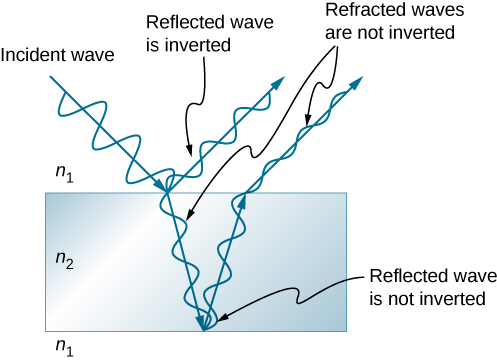
If the film in Figure \PageIndex{3} is a soap bubble (essentially water with air on both sides), then a phase shift of λ/2 occurs for ray 1 but not for ray 2. Thus, when the film is very thin and the path length difference between the two rays is negligible, they are exactly out of phase, and destructive interference occurs at all wavelengths. Thus, the soap bubble is dark here. The thickness of the film relative to the wavelength of light is the other crucial factor in thin-film interference. Ray 2 in Figure \PageIndex{3} travels a greater distance than ray 1. For light incident perpendicular to the surface, ray 2 travels a distance approximately 2t farther than ray 1. When this distance is an integral or half-integral multiple of the wavelength in the medium (\lambda_n = \lambda/n, where λ is the wavelength in vacuum and n is the index of refraction), constructive or destructive interference occurs, depending also on whether there is a phase change in either ray.
Sophisticated cameras use a series of several lenses. Light can reflect from the surfaces of these various lenses and degrade image clarity. To limit these reflections, lenses are coated with a thin layer of magnesium fluoride, which causes destructive thin-film interference. What is the thinnest this film can be, if its index of refraction is 1.38 and it is designed to limit the reflection of 550-nm light, normally the most intense visible wavelength? Assume the index of refraction of the glass is 1.52.
Strategy
Refer to Figure \PageIndex{2} and use n_1 = 1.00 for air, n_2 = 1.38, and n_3 = 1.52. Both ray 1 and ray 2 have a λ/2 shift upon reflection. Thus, to obtain destructive interference, ray 2 needs to travel a half wavelength farther than ray 1. For rays incident perpendicularly, the path length difference is 2t.
Solution
To obtain destructive interference here,
2t = \dfrac{\lambda_{n2}}{2} \nonumber
where \lambda_{n2} is the wavelength in the film and is given by \lambda_{n2} = \lambda / n_2. Thus,
2t = \dfrac{\lambda/n_2}{2}. \nonumber
Solving for t and entering known values yields
t = \dfrac{\lambda/n_2}{4} = \dfrac{(500 \, nm)/1.38}{4} = 99.6 \, nm. \nonumber
Significance
Films such as the one in this example are most effective in producing destructive interference when the thinnest layer is used, since light over a broader range of incident angles is reduced in intensity. These films are called nonreflective coatings; this is only an approximately correct description, though, since other wavelengths are only partially cancelled. Nonreflective coatings are also used in car windows and sunglasses.
Combining Path Length Difference with Phase Change
Thin-film interference is most constructive or most destructive when the path length difference for the two rays is an integral or half-integral wavelength. That is, for rays incident perpendicularly,
2t = \lambda_n, \, 2\lambda_n, \, 3\lambda_n, ... \, or \, 2t = \lambda_n/2, \, 3\lambda_n/2, \, 5\lambda_n/2, ... \nonumber
To know whether interference is constructive or destructive, you must also determine if there is a phase change upon reflection. Thin-film interference thus depends on film thickness, the wavelength of light, and the refractive indices. For white light incident on a film that varies in thickness, you can observe rainbow colors of constructive interference for various wavelengths as the thickness varies.
- What are the three smallest thicknesses of a soap bubble that produce constructive interference for red light with a wavelength of 650 nm? The index of refraction of soap is taken to be the same as that of water.
- What three smallest thicknesses give destructive interference?
Strategy
Use Figure \PageIndex{3} to visualize the bubble, which acts as a thin film between two layers of air. Thus n_1 = n_3 = 1.00 for air, and n_2 = 1.333 for soap (equivalent to water). There is a λ/2 shift for ray 1 reflected from the top surface of the bubble and no shift for ray 2 reflected from the bottom surface. To get constructive interference, then, the path length difference (2t) must be a half-integral multiple of the wavelength—the first three being \lambda_n/2, \, 3\lambda_n/2, and 5\lambda_n/2. To get destructive interference, the path length difference must be an integral multiple of the wavelength—the first three being 0, \lambda_n, and 2\lambda_n.
Solution
a. Constructive interference occurs here when
2t_c = \dfrac{\lambda_n}{2}, \, \dfrac{3\lambda_n}{2}, \, \dfrac{5\lambda_n}{2}, ... \nonumber
Thus, the smallest constructive thickness t_c is
t_c = \dfrac{\lambda_n}{4} = \dfrac{\lambda/n}{4} = \dfrac{(650 \, nm)/1.333}{4} = 122 \, nm. \nonumber
The next thickness that gives constructive interference is t'_c = 3\lambda_n/4, so that
t'_c = 366 \, nm. \nonumber
Finally, the third thickness producing constructive interference is t'_c = 5\lambda_n/4, so that
t'_c = 610 \, nm. \nonumber
b. For destructive interference, the path length difference here is an integral multiple of the wavelength. The first occurs for zero thickness, since there is a phase change at the top surface, that is,
t_d = 0, \nonumber
the very thin (or negligibly thin) case discussed above. The first non-zero thickness producing destructive interference is
2t'_d = \lambda_n. \nonumber
Substituting known values gives
t'_d = \dfrac{\lambda}{2} = \dfrac{\lambda/n}{2} = \dfrac{(650 \, nm)/1.333}{2} = 244 \, nm. \nonumber
Finally, the third destructive thickness is 2t''_d = 2\lambda_n, so that
t''_d = \lambda_n = \dfrac{\lambda}{n} = \dfrac{650 \, nm}{1.333} = 488 \, nm. \nonumber
Significance
If the bubble were illuminated with pure red light, we would see bright and dark bands at very uniform increases in thickness. First would be a dark band at 0 thickness, then bright at 122 nm thickness, then dark at 244 nm, bright at 366 nm, dark at 488 nm, and bright at 610 nm. If the bubble varied smoothly in thickness, like a smooth wedge, then the bands would be evenly spaced.
Going further with Example \PageIndex{2}, what are the next two thicknesses of soap bubble that would lead to
- constructive interference, and
- destructive interference?
- Answer a
-
853 nm and 1097 nm
- Answer b
-
731 nm and 975 nm
Another example of thin-film interference can be seen when microscope slides are separated (see Figure \PageIndex{4}). The slides are very flat, so that the wedge of air between them increases in thickness very uniformly. A phase change occurs at the second surface but not the first, so a dark band forms where the slides touch. The rainbow colors of constructive interference repeat, going from violet to red again and again as the distance between the slides increases. As the layer of air increases, the bands become more difficult to see, because slight changes in incident angle have greater effects on path length differences. If monochromatic light instead of white light is used, then bright and dark bands are obtained rather than repeating rainbow colors.
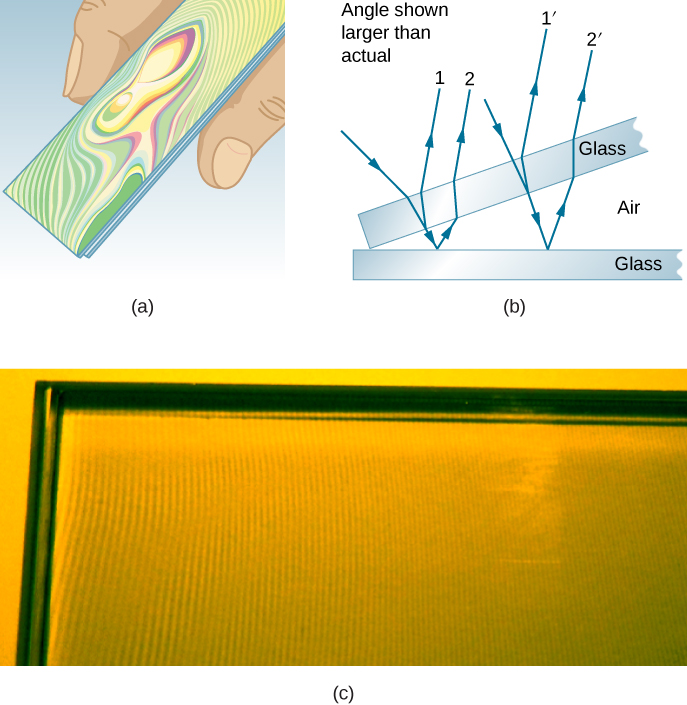
An important application of thin-film interference is found in the manufacturing of optical instruments. A lens or mirror can be compared with a master as it is being ground, allowing it to be shaped to an accuracy of less than a wavelength over its entire surface. Figure \PageIndex{5} illustrates the phenomenon called Newton’s rings, which occurs when the plane surfaces of two lenses are placed together. (The circular bands are called Newton’s rings because Isaac Newton described them and their use in detail. Newton did not discover them; Robert Hooke did, and Newton did not believe they were due to the wave character of light.) Each successive ring of a given color indicates an increase of only half a wavelength in the distance between the lens and the blank, so that great precision can be obtained. Once the lens is perfect, no rings appear.

Thin-film interference has many other applications, both in nature and in manufacturing. The wings of certain moths and butterflies have nearly iridescent colors due to thin-film interference. In addition to pigmentation, the wing’s color is affected greatly by constructive interference of certain wavelengths reflected from its film-coated surface. Some car manufacturers offer special paint jobs that use thin-film interference to produce colors that change with angle. This expensive option is based on variation of thin-film path length differences with angle. Security features on credit cards, banknotes, driving licenses, and similar items prone to forgery use thin-film interference, diffraction gratings, or holograms. As early as 1998, Australia led the way with dollar bills printed on polymer with a diffraction grating security feature, making the currency difficult to forge. Other countries, such as Canada, New Zealand, and Taiwan, are using similar technologies, while US currency includes a thin-film interference effect.


