5.8: Doppler Effect for Light
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain the origin of the shift in frequency and wavelength of the observed wavelength when observer and source moved toward or away from each other
- Derive an expression for the relativistic Doppler shift
- Apply the Doppler shift equations to real-world examples
As discussed in the chapter on sound, if a source of sound and a listener are moving farther apart, the listener encounters fewer cycles of a wave in each second, and therefore lower frequency, than if their separation remains constant. For the same reason, the listener detects a higher frequency if the source and listener are getting closer. The resulting Doppler shift in detected frequency occurs for any form of wave. For sound waves, however, the equations for the Doppler shift differ markedly depending on whether it is the source, the observer, or the air, which is moving. Light requires no medium, and the Doppler shift for light traveling in vacuum depends only on the relative speed of the observer and source.
The Relativistic Doppler Effect
Suppose an observer in S sees light from a source in S′ moving away at velocity v (Figure 5.8.1). The wavelength of the light could be measured within S′ — for example, by using a mirror to set up standing waves and measuring the distance between nodes. These distances are proper lengths with S′ as their rest frame, and change by a factor √1−v2/c2 when measured in the observer’s frame S, where the ruler measuring the wavelength in S′ is seen as moving.
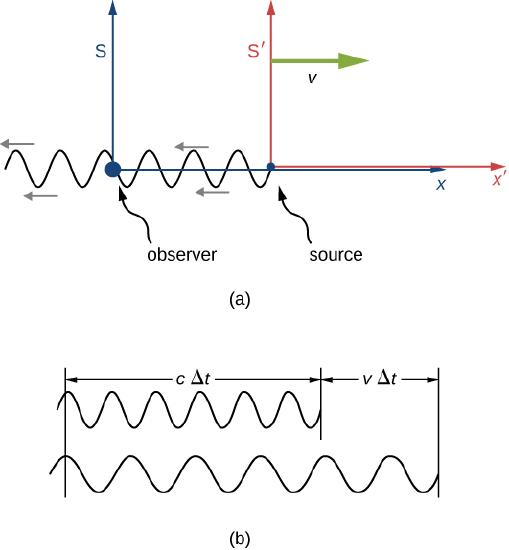
If the source were stationary in S, the observer would see a length cΔt of the wave pattern in time Δt. But because of the motion of S' relative to S, considered solely within S, the observer sees the wave pattern, and therefore the wavelength, stretched out by a factor of
cΔtperiod+vΔtperiodcΔtperiod=1+vc
as illustrated in (b) of Figure 5.8.1. The overall increase from both effects gives
λobs=λsrc(1+vc)√11−v2c2=λsrc(1+vc)√1(1+vc)(1−vc)=λsrc√(1+vc)(1−vc)
where λsrc is the wavelength of the light seen by the source in S' and λobs is the wavelength that the observer detects within S.
Red Shifts and Blue Shifts
The observed wavelength λobs of electromagnetic radiation is longer (called a “red shift”) than that emitted by the source when the source moves away from the observer. Similarly, the wavelength is shorter (called a “blue shift”) when the source moves toward the observer. The amount of change is determined by
λobs=λs√(1+vc)(1−vc)
where λs is the wavelength in the frame of reference of the source, and v is the relative velocity of the two frames S and S′. The velocity v is positive for motion away from an observer and negative for motion toward an observer. In terms of source frequency and observed frequency, this equation can be written as
fobs=fs√(1−vc)(1+vc)
Notice that the signs are different from those of the wavelength equation.
Suppose a galaxy is moving away from Earth at a speed 0.825c. It emits radio waves with a wavelength of
0.525 m. What wavelength would we detect on Earth?
Strategy
Because the galaxy is moving at a relativistic speed, we must determine the Doppler shift of the radio waves using the relativistic Doppler shift instead of the classical Doppler shift.
Solution
- Identify the knowns: u=0.825c; λs=0.525m.
- Identify the unknown: λobs.
- Express the answer as an equation:
λobs=λs√1+vc1−vc.
- Do the calculation:
λobs=λs√1+vc1−vc=(0.525m)√1+0.825cc1−0.825cc=1.70m.
Significance
Because the galaxy is moving away from Earth, we expect the wavelengths of radiation it emits to be redshifted. The wavelength we calculated is 1.70 m, which is redshifted from the original wavelength of 0.525 m. You will see in Particle Physics and Cosmology that detecting redshifted radiation led to present-day understanding of the origin and evolution of the universe.
Suppose a space probe moves away from Earth at a speed 0.350c. It sends a radio-wave message back to Earth at a frequency of 1.50 GHz. At what frequency is the message received on Earth?
Solution
We can substitute the data directly into the equation for relativistic Doppler frequency (Equation ???):
fobs=fs√1−vc1+vc=(1.50GHz)√1−0.350cc1+0.350cc=1.04GHz.
The relativistic Doppler effect has applications ranging from Doppler radar storm monitoring to providing information on the motion and distance of stars. We describe some of these applications in the exercises.


