5.5: The Doppler Shift

Last updated
Save as PDF

Page ID: 32951

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

You have probably heard how the pitch of a train horn changes as it passes you. When the train is approaching, the pitch or frequency is higher than when it is moving away from you. This is called the Doppler shift. A similar, but distinct shift occurs if you are moving past a source of sound. If a stationary whistle is blowing, the pitch perceived from a moving car is higher while moving toward the source than when moving away. The first case thus has a moving source, while the second case has a moving observer.

Figure 5.3: Definition sketch for computing the Doppler shift for light.

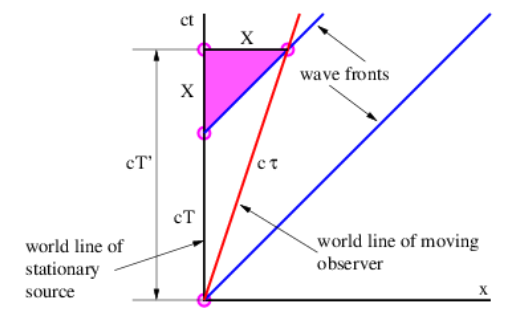
In this section we compute the Doppler shift as it applies to light moving through a vacuum. Figure 5.3 shows the geometry for computing the time between wave fronts of light for a stationary and a moving reference frame. The time in the stationary frame is just T. Since the world lines of the wave fronts have a slope of unity, the sides of the shaded triangle have the same value, X. If the observer is moving at speed U, the slope of the observer’s world line is c∕U, which means that \(\mathrm{c} / \mathrm{U}=(\mathrm{cT}+\mathrm{X}) / \mathrm{X}\). Solving this for X yields \(\mathrm{X}=\mathrm{UT} /(1-\mathrm{U} / \mathrm{c})\), which can then be used to compute \(\mathrm{T}^{\prime}=\mathrm{T}+\mathrm{X} / \mathrm{c}=\mathrm{T} /(1-\mathrm{U} / \mathrm{c})\). This formula as it stands leads to the classical Doppler shift for a moving observer. However, with relativistic velocities, one additional factor needs to be taken into account: The observer experiences time dilation since he or she is moving. The actual time measured by the observer between wave fronts is actually

\[\begin{align} \tau &=\left(T^{\prime 2}-X^{2} / c^{2}\right)^{1 / 2} \\[4pt] &=T \frac{\left(1-U^{2} / c^{2}\right)^{1 / 2}}{1-U / c} \\[4pt] &=T\left(\frac{1+U / c}{1-U / c}\right)^{1 / 2}\label{5.14} \end{align}\]

where the last step uses \(1-\mathrm{U}^{2} / \mathrm{c}^{2}=(1-\mathrm{U} / \mathrm{c})(1+\mathrm{U} / \mathrm{c})\). From this we infer the relativistic Doppler shift formula for light in a vacuum:

\[\omega^{\prime}=\omega\left(\frac{1-U / c}{1+U / c}\right)^{1 / 2}\label{5.15}\]

where the frequency measured by the moving observer is \(\omega^{\prime}=2 \pi / \mathrm{T}\) and the frequency observed in the stationary frame is \(\omega=2 \pi / T\).

We could go on to determine the Doppler shift resulting from a moving source. However, by the principle of relativity, the laws of physics should be the same in the reference frame in which the observer is stationary and the source is moving. Furthermore, the speed of light is still c in that frame. Therefore, the problem of a stationary observer and a moving source is conceptually the same as the problem of a moving observer and a stationary source when the wave is moving at speed \(c\). This is unlike the case for, say, sound waves, where the stationary observer and the stationary source yield different formulas for the Doppler shift.