13.5: Satellite Orbits and Energy
- Page ID
- 4051
- Describe the mechanism for circular orbits
- Find the orbital periods and speeds of satellites
- Determine whether objects are gravitationally bound
The Moon orbits Earth. In turn, Earth and the other planets orbit the Sun. The space directly above our atmosphere is filled with artificial satellites in orbit. We examine the simplest of these orbits, the circular orbit, to understand the relationship between the speed and period of planets and satellites in relation to their positions and the bodies that they orbit.
Circular Orbits
As noted at the beginning of this chapter, Nicolaus Copernicus first suggested that Earth and all other planets orbit the Sun in circles. He further noted that orbital periods increased with distance from the Sun. Later analysis by Kepler showed that these orbits are actually ellipses, but the orbits of most planets in the solar system are nearly circular. Earth’s orbital distance from the Sun varies a mere 2%. The exception is the eccentric orbit of Mercury, whose orbital distance varies nearly 40%.
Determining the orbital speed and orbital period of a satellite is much easier for circular orbits, so we make that assumption in the derivation that follows. As we described in the previous section, an object with negative total energy is gravitationally bound and therefore is in orbit. Our computation for the special case of circular orbits will confirm this. We focus on objects orbiting Earth, but our results can be generalized for other cases.
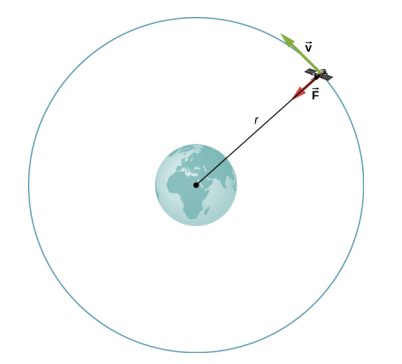
Consider a satellite of mass m in a circular orbit about Earth at distance \(r\) from the center of Earth (Figure \(\PageIndex{1}\)). It has centripetal acceleration directed toward the center of Earth. Earth’s gravity is the only force acting, so Newton’s second law gives
\[\frac{GmM_{E}}{r^{2}} = ma_{c} = \frac{mv_{orbit}^{2}}{r} \ldotp\]
We solve for the speed of the orbit, noting that \(m\) cancels, to get the orbital speed
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} \ldotp \label{13.7}\]
Consistent with what we saw in \(g = G \frac{M_E}{r^2}\) and \(v_{esc} = \sqrt{\frac{2GM}{R}}\), m does not appear in Equation \ref{13.7}. The value of g, the escape velocity, and orbital velocity depend only upon the distance from the center of the planet, and not upon the mass of the object being acted upon. Notice the similarity in the equations for vorbit and vesc. The escape velocity is exactly \(\sqrt{2}\) times greater, about 40%, than the orbital velocity. This comparison was noted in Example 13.4.2, and it is true for a satellite at any radius.
To find the period of a circular orbit, we note that the satellite travels the circumference of the orbit \( 2\pi r\) in one period \(T\). Using the definition of speed, we have
\[v_{orbit} = \frac{2 \pi r}{T}.\]
We substitute this into Equation \ref{13.7} and rearrange to get
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.8}\]
We see in the next section that this represents Kepler’s third law for the case of circular orbits. It also confirms Copernicus’s observation that the period of a planet increases with increasing distance from the Sun. We need only replace \(M_E\) with \(M_{Sun}\) in Equation \ref{13.8}.
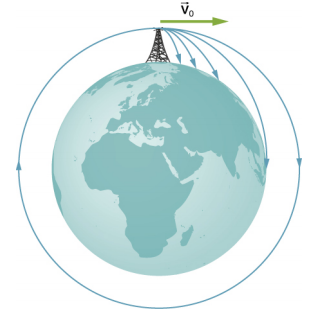
We conclude this section by returning to our earlier discussion about astronauts in orbit appearing to be weightless, as if they were free-falling towards Earth. In fact, they are in free fall. Consider the trajectories shown in Figure \(\PageIndex{2}\). (This figure is based on a drawing by Newton in his Principia and also appeared earlier in Motion in Two and Three Dimensions.) All the trajectories shown that hit the surface of Earth have less than orbital velocity. The astronauts would accelerate toward Earth along the noncircular paths shown and feel weightless. (Astronauts actually train for life in orbit by riding in airplanes that free fall for 30 seconds at a time.) But with the correct orbital velocity, Earth’s surface curves away from them at exactly the same rate as they fall toward Earth. Of course, staying the same distance from the surface is the point of a circular orbit.
We can summarize our discussion of orbiting satellites in the following Problem-Solving Strategy.
- Determine whether the equations for speed, energy, or period are valid for the problem at hand. If not, start with the first principles we used to derive those equations.
- To start from first principles, draw a free-body diagram and apply Newton’s law of gravitation and Newton’s second law.
- Along with the definitions for speed and energy, apply Newton’s second law of motion to the bodies of interest.
Determine the orbital speed and period for the International Space Station (ISS).
Strategy
Since the ISS orbits 4.00 x 102 km above Earth’s surface, the radius at which it orbits is RE + 4.00 x 102 km. We use Equations \ref{13.7} and \ref{13.8} to find the orbital speed and period, respectively.
Solution
Using Equation \ref{13.7}, the orbital velocity is
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} = \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} = 7.67 \times 10^{3}\; m/s\]
which is about 17,000 mph. Using Equation \ref{13.8}, the period is
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} = 2 \pi \sqrt{\frac{(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}} = 5.55 \times 10^{3}\; s\]
which is just over 90 minutes.
Significance
The ISS is considered to be in low Earth orbit (LEO). Nearly all satellites are in LEO, including most weather satellites. GPS satellites, at about 20,000 km, are considered medium Earth orbit. The higher the orbit, the more energy is required to put it there and the more energy is needed to reach it for repairs. Of particular interest are the satellites in geosynchronous orbit. All fixed satellite dishes on the ground pointing toward the sky, such as TV reception dishes, are pointed toward geosynchronous satellites. These satellites are placed at the exact distance, and just above the equator, such that their period of orbit is 1 day. They remain in a fixed position relative to Earth’s surface.
By what factor must the radius change to reduce the orbital velocity of a satellite by one-half? By what factor would this change the period?
Determine the mass of Earth from the orbit of the Moon.
Strategy
We use Equation \ref{13.8}, solve for ME, and substitute for the period and radius of the orbit. The radius and period of the Moon’s orbit was measured with reasonable accuracy thousands of years ago. From the astronomical data in Appendix D, the period of the Moon is 27.3 days = 2.36 x 106 s, and the average distance between the centers of Earth and the Moon is 384,000 km.
Solution
Solving for \(M_E\),
\[\begin{split} T & = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \\ M_{E} & = \frac{2 \pi^{2} r^{3}}{GT^{2}} = \frac{4 \pi^{2} (3.84 \times 10^{8}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.36 \times 10^{6}\; s)^{2}} = 6.01 \times 10^{24}\; kg \ldotp \end{split}\]
Significance
Compare this to the value of 5.96 x 1024 kg that we obtained in Example 13.3.3, using the value of \(g\) at the surface of Earth. Although these values are very close (~0.8%), both calculations use average values. The value of g varies from the equator to the poles by approximately 0.5%. But the Moon has an elliptical orbit in which the value of r varies just over 10%. (The apparent size of the full Moon actually varies by about this amount, but it is difficult to notice through casual observation as the time from one extreme to the other is many months.)
There is another consideration to this last calculation of ME. We derived Equation \ref{13.8} assuming that the satellite orbits around the center of the astronomical body at the same radius used in the expression for the gravitational force between them. What assumption is made to justify this? Earth is about 81 times more massive than the Moon. Does the Moon orbit about the exact center of Earth?
Let’s revisit Example 13.2.2. Assume that the Milky Way and Andromeda galaxies are in a circular orbit about each other. What would be the velocity of each and how long would their orbital period be? Assume the mass of each is 800 billion solar masses and their centers are separated by 2.5 million light years.
Strategy
We cannot use Equations \ref{13.7} and \ref{13.8} directly because they were derived assuming that the object of mass m orbited about the center of a much larger planet of mass M. We determined the gravitational force in Example 13.2.2 using Newton’s law of universal gravitation. We can use Newton’s second law, applied to the centripetal acceleration of either galaxy, to determine their tangential speed. From that result we can determine the period of the orbit.
Solution
In Example 13.2.2, we found the force between the galaxies to be
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})\frac{[(800 \times 10^{9})(2.0 \times 10^{30})\; kg]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15})\; m]^{2}} = 3.0 \times 10^{29}\; N\]
and that the acceleration of each galaxy is
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30})\; kg} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
Since the galaxies are in a circular orbit, they have centripetal acceleration. If we ignore the effect of other galaxies, then, as we learned in Linear Momentum and Collisions and Fixed-Axis Rotation, the centers of mass of the two galaxies remain fixed. Hence, the galaxies must orbit about this common center of mass. For equal masses, the center of mass is exactly half way between them. So the radius of the orbit, rorbit, is not the same as the distance between the galaxies, but one-half that value, or 1.25 million light-years. These two different values are shown in Figure \(\PageIndex{3}\).

Using the expression for centripetal acceleration, we have
\[\begin{split} a_{c} & = \frac{v_{orbit}^{2}}{r_{orbit}} \\ 1.9 \times 10^{-13}\; m/s^{2} & = \frac{v_{orbit}^{2}}{(1.25 \times 10^{6})(9.5 \times 10^{15})\; m} \ldotp \end{split}\]
Solving for the orbit velocity, we have \(v_{orbit} = 47\, km/s\). Finally, we can determine the period of the orbit directly from
\[T = \frac{2 \pi r}{v_{orbit}}\]
to find that the period is T = 1.6 x 1018 s, about 50 billion years.
Significance
The orbital speed of 47 km/s might seem high at first. But this speed is comparable to the escape speed from the Sun, which we calculated in an earlier example. To give even more perspective, this period is nearly four times longer than the time that the Universe has been in existence.
In fact, the present relative motion of these two galaxies is such that they are expected to collide in about 4 billion years. Although the density of stars in each galaxy makes a direct collision of any two stars unlikely, such a collision will have a dramatic effect on the shape of the galaxies. Examples of such collisions are well known in astronomy
Galaxies are not single objects. How does the gravitational force of one galaxy exerted on the “closer” stars of the other galaxy compare to those farther away? What effect would this have on the shape of the galaxies themselves?
See the Sloan Digital Sky Survey page for more information on colliding galaxies.
Use this interactive simulation to move the Sun, Earth, Moon, and space station to see the effects on their gravitational forces and orbital paths. Visualize the sizes and distances between different heavenly bodies, and turn off gravity to see what would happen without it.
Energy in Circular Orbits
In Gravitational Potential Energy and Total Energy, we argued that objects are gravitationally bound if their total energy is negative. The argument was based on the simple case where the velocity was directly away or toward the planet. We now examine the total energy for a circular orbit and show that indeed, the total energy is negative. As we did earlier, we start with Newton’s second law applied to a circular orbit,
\[\begin{split} \frac{GmM_{E}}{r^{2}} & = ma_{c} = \frac{mv^{2}}{r} \\ \frac{GmM_{E}}{r} & = mv^{2} \ldotp \end{split}\]
In the last step, we multiplied by \(r\) on each side. The right side is just twice the kinetic energy, so we have
\[K = \frac{1}{2} mv^{2} = \frac{GmM_{E}}{2r} \ldotp\]
The total energy is the sum of the kinetic and potential energies, so our final result is
\[E = K + U = \frac{GmM_{E}}{2r} - \frac{GmM_{E}}{r} = - \frac{GmM_{E}}{2r} \ldotp \label{13.9}\]
We can see that the total energy is negative, with the same magnitude as the kinetic energy. For circular orbits, the magnitude of the kinetic energy is exactly one-half the magnitude of the potential energy. Remarkably, this result applies to any two masses in circular orbits about their common center of mass, at a distance r from each other. The proof of this is left as an exercise. We will see in the next section that a very similar expression applies in the case of elliptical orbits.
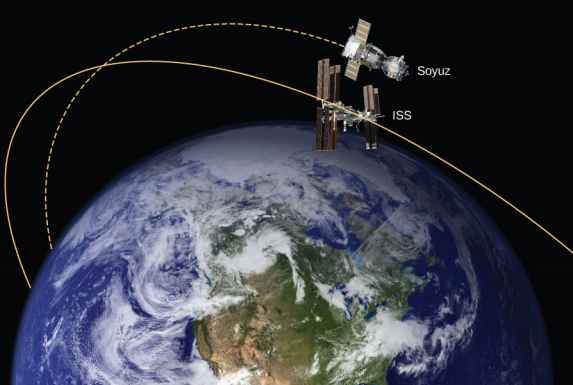
In Example 13.4.1, we calculated the energy required to simply lift the 9000-kg Soyuz vehicle from Earth’s surface to the height of the ISS, 400 km above the surface. In other words, we found its change in potential energy. We now ask, what total energy change in the Soyuz vehicle is required to take it from Earth’s surface and put it in orbit with the ISS for a rendezvous (Figure \(\PageIndex{4}\))? How much of that total energy is kinetic energy?
Strategy
The energy required is the difference in the Soyuz’s total energy in orbit and that at Earth’s surface. We can use Equation \ref{13.9} to find the total energy of the Soyuz at the ISS orbit. But the total energy at the surface is simply the potential energy, since it starts from rest. [Note that we do not use Equation \ref{13.9} at the surface, since we are not in orbit at the surface.] The kinetic energy can then be found from the difference in the total energy change and the change in potential energy found in Example 13.4.1. Alternatively, we can use Equation \ref{13.7} to find vorbit and calculate the kinetic energy directly from that. The total energy required is then the kinetic energy plus the change in potential energy found in Example 13.4.1.
Solution
From Equation \ref{13.9}, the total energy of the Soyuz in the same orbit as the ISS is
\[\begin{split} E_{orbit} & = K_{orbit} + U_{orbit} = - \frac{GmM_{E}}{2r} \\ & = \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{2(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)} = -2.65 \times 10^{11}\; J \ldotp \end{split}\]
The total energy at Earth's surface is
\[\begin{split} E_{surface} & = K_{surface} + U_{surface} = 0 - \frac{GmM_{E}}{r} \\ & = - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6}\; m)} \\ & = -5.63 \times 10^{11}\; J \ldotp \end{split}\]
The change in energy is
\[\Delta E = E_{orbit}− E_{surface} = 2.98 x 10^{11}\, J. \nonumber\]
To get the kinetic energy, we subtract the change in potential energy from Example 13.4.1, \(\Delta\)U = 3.32 x 1010 J. That gives us Korbit = (2.98 x 1011) − (3.32 x 1010) = 2.65 x 1011 J. As stated earlier, the kinetic energy of a circular orbit is always one-half the magnitude of the potential energy, and the same as the magnitude of the total energy. Our result confirms this.
The second approach is to use Equation \ref{13.7} to find the orbital speed of the Soyuz, which we did for the ISS in Example \(\PageIndex{1}\).
\[ \begin{align*} v_{orbit} &= \sqrt{\frac{GM_{E}}{r}} \\[4pt]&= \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} \\[4pt] &= 7.67 \times 10^{3}\; m/s \end{align*}\]
So the kinetic energy of the Soyuz in orbit is
\[ \begin{align*}K_{orbit} &= \frac{1}{2} mv_{orbit}^{2} \\[4pt]&= \frac{1}{2} (9000\; kg)(7.67 \times 10^{3}\; m/s)^{2} \\[4pt]&= 2.65 \times 10^{11}\; J,\end{align*}\]
the same as in the previous method. The total energy is just
\[ \begin{align*}E_{orbit} &= K_{orbit} + \Delta U \\[4pt]&= (2.65 \times 10^{11}) + (3.32 \times 10^{10}) \\[4pt]&= 2.95 \times 10^{11}\; J \ldotp\end{align*}\]
Significance
The kinetic energy of the Soyuz is nearly eight times the change in its potential energy, or 90% of the total energy needed for the rendezvous with the ISS. And it is important to remember that this energy represents only the energy that must be given to the Soyuz. With our present rocket technology, the mass of the propulsion system (the rocket fuel, its container and combustion system) far exceeds that of the payload, and a tremendous amount of kinetic energy must be given to that mass. So the actual cost in energy is many times that of the change in energy of the payload itself.


