14.3: Fluids, Density, and Pressure (Part 2)
- Page ID
- 6553
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Variation of pressure with depth in a fluid of constant density
Pressure is defined for all states of matter, but it is particularly important when discussing fluids. An important characteristic of fluids is that there is no significant resistance to the component of a force applied parallel to the surface of a fluid. The molecules of the fluid simply flow to accommodate the horizontal force. A force applied perpendicular to the surface compresses or expands the fluid. If you try to compress a fluid, you find that a reaction force develops at each point inside the fluid in the outward direction, balancing the force applied on the molecules at the boundary.
Consider a fluid of constant density as shown in Figure \(\PageIndex{1}\). The pressure at the bottom of the container is due to the pressure of the atmosphere (p0) plus the pressure due to the weight of the fluid. The pressure due to the fluid is equal to the weight of the fluid divided by the area. The weight of the fluid is equal to its mass times the acceleration due to gravity.
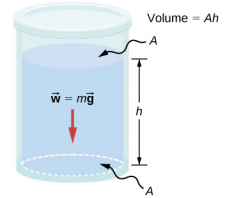
Since the density is constant, the weight can be calculated using the density:
\[w = mg = \rho Vg = \rho Ahg \ldotp\]
The pressure at the bottom of the container is therefore equal to atmospheric pressure added to the weight of the fluid divided by the area:
\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]
This equation is only good for pressure at a depth for a fluid of constant density
The pressure at a depth in a fluid of constant density is equal to the pressure of the atmosphere plus the pressure due to the weight of the fluid, or
\[p = p_{0} + \rho hg, \label{14.4}\]
Where p is the pressure at a particular depth, p0 is the pressure of the atmosphere, \(\rho\) is the density of the fluid, g is the acceleration due to gravity, and h is the depth.

Consider the pressure and force acting on the dam retaining a reservoir of water (Figure \(\PageIndex{2}\)). Suppose the dam is 500-m wide and the water is 80.0-m deep at the dam, as illustrated below. (a) What is the average pressure on the dam due to the water? (b) Calculate the force exerted against the dam.
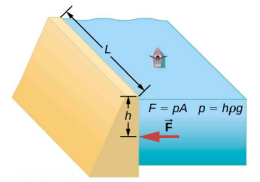
The average pressure p due to the weight of the water is the pressure at the average depth h of 40.0 m, since pressure increases linearly with depth. The force exerted on the dam by the water is the average pressure times the area of contact, F = pA.
Solution
- The average pressure due to the weight of a fluid is $$p = h \rho g \ldotp \label{14.5}$$Entering the density of water from Table 14.1 and taking h to be the average depth of 40.0 m, we obtain $$\begin{split} p & = (40.0\; m)(10^{3}\; kg/m^{3})(9.80\; m/s^{2}) \\ & = 3.92 \times 10^{5}\; N/m^{2} = 392\; kPa \ldotp \end{split}$$
- We have already found the value for p. The area of the dam is $$A = (80.0\; m) \times (500\; m) = 4.00 \times 10^{4}\; m^{2} \ldotp$$so that $$\begin{split} F & = (3.92 \times 10^{5}\; N/m^{2})(4.00 \times 10^{4}\; m^{2}) \\ & = 1.57 \times 10^{10}\; M \ldotp \end{split}$$
Significance
Although this force seems large, it is small compared with the 1.96 x 1013 N weight of the water in the reservoir. In fact, it is only 0.0800% of the weight.
If the reservoir in Example \(\PageIndex{1}\) covered twice the area, but was kept to the same depth, would the dam need to be redesigned?
Pressure in a static fluid in a uniform gravitational field
A static fluid is a fluid that is not in motion. At any point within a static fluid, the pressure on all sides must be equal—otherwise, the fluid at that point would react to a net force and accelerate.
The pressure at any point in a static fluid depends only on the depth at that point. As discussed, pressure in a fluid near Earth varies with depth due to the weight of fluid above a particular level. In the above examples, we assumed density to be constant and the average density of the fluid to be a good representation of the density. This is a reasonable approximation for liquids like water, where large forces are required to compress the liquid or change the volume. In a swimming pool, for example, the density is approximately constant, and the water at the bottom is compressed very little by the weight of the water on top. Traveling up in the atmosphere is quite a different situation, however. The density of the air begins to change significantly just a short distance above Earth’s surface.
To derive a formula for the variation of pressure with depth in a tank containing a fluid of density \(\rho\) on the surface of Earth, we must start with the assumption that the density of the fluid is not constant. Fluid located at deeper levels is subjected to more force than fluid nearer to the surface due to the weight of the fluid above it. Therefore, the pressure calculated at a given depth is different than the pressure calculated using a constant density.
Imagine a thin element of fluid at a depth h, as shown in Figure \(\PageIndex{3}\). Let the element have a cross-sectional area A and height \(\Delta\)y. The forces acting upon the element are due to the pressures p(y) above and p(y + \(\Delta\)y) below it. The weight of the element itself is also shown in the free-body diagram.
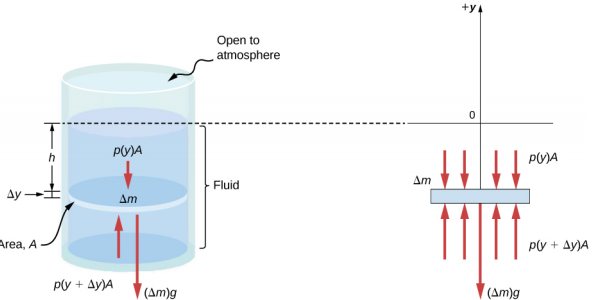
Since the element of fluid between y and y + \(\Delta\)y is not accelerating, the forces are balanced. Using a Cartesian y-axis oriented up, we find the following equation for the y-component:
\[p(y + \Delta y)A - p(y)A - g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]
Note that if the element had a non-zero y-component of acceleration, the right-hand side would not be zero but would instead be the mass times the y-acceleration. The mass of the element can be written in terms of the density of the fluid and the volume of the elements:
\[\Delta m = |\rho A \Delta y| = - \rho A \Delta y \quad (\Delta y < 0) \ldotp\]
Putting this expression for \(\Delta\)m into Equation \ref{14.6} and then dividing both sides by A\(\Delta\)y, we find
\[\frac{p(y + \Delta y) - p(y)}{\Delta y} = - \rho g \ldotp \label{14.7}\]
Taking the limit of the infinitesimally thin element \(\Delta\)y → 0, we obtain the following differential equation, which gives the variation of pressure in a fluid:
\[\frac{dp}{dy} = - \rho g \ldotp \label{14.8}\]
This equation tells us that the rate of change of pressure in a fluid is proportional to the density of the fluid. The solution of this equation depends upon whether the density \(\rho\) is constant or changes with depth; that is, the function \(\rho\)(y).
If the range of the depth being analyzed is not too great, we can assume the density to be constant. But if the range of depth is large enough for the density to vary appreciably, such as in the case of the atmosphere, there is significant change in density with depth. In that case, we cannot use the approximation of a constant density.
Pressure in a fluid with a constant density
Let’s use Equation \ref{14.9} to work out a formula for the pressure at a depth h from the surface in a tank of a liquid such as water, where the density of the liquid can be taken to be constant.
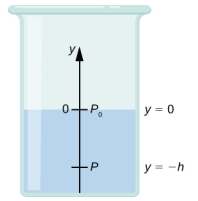
We need to integrate Equation \ref{14.9} from y = 0, where the pressure is atmospheric pressure (p0), to y = −h, the y-coordinate of the depth:
\[\begin{split} \int_{p_{0}}^{p} dp & = - \int_{0}^{-h} \rho gdy \\ p - p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14.9}\]
Hence, pressure at a depth of fluid on the surface of Earth is equal to the atmospheric pressure plus \(\rho\)gh if the density of the fluid is constant over the height, as we found previously.
Note that the pressure in a fluid depends only on the depth from the surface and not on the shape of the container. Thus, in a container where a fluid can freely move in various parts, the liquid stays at the same level in every part, regardless of the shape, as shown in Figure \(\PageIndex{4}\).

Variation of atmospheric pressure with height
The change in atmospheric pressure with height is of particular interest. Assuming the temperature of air to be constant, and that the ideal gas law of thermodynamics describes the atmosphere to a good approximation, we can find the variation of atmospheric pressure with height, when the temperature is constant. (We discuss the ideal gas law in a later chapter, but we assume you have some familiarity with it from high school and chemistry.) Let p(y) be the atmospheric pressure at height y. The density \(\rho\) at y, the temperature T in the Kelvin scale (K), and the mass m of a molecule of air are related to the absolute pressure by the ideal gas law, in the form
\[p = \rho \frac{k_{B} T}{m}\; (atmosphere), \label{14.10}\]
where kB is Boltzmann’s constant, which has a value of 1.38 x 10−23 J/K.
You may have encountered the ideal gas law in the form pV = nRT, where n is the number of moles and R is the gas constant. Here, the same law has been written in a different form, using the density \(\rho\) instead of volume V. Therefore, if pressure p changes with height, so does the density \(\rho\). Using density from the ideal gas law, the rate of variation of pressure with height is given as
\[\frac{dp}{dy} = -p \left(\dfrac{mg}{k_{B} T}\right),\]
where constant quantities have been collected inside the parentheses. Replacing these constants with a single symbol \(\alpha\), the equation looks much simpler:
\[\begin{split} \frac{dp}{dy} & = - \alpha p \\ \frac{dp}{p} & = - \alpha dy \\ \int_{p_{0}}^{p(y)} \frac{dp}{p} & = \int_{0}^{y} - \alpha dy \\ [\ln (p)]_{p_{0}}^{p(y)} & = [- \alpha y]_{0}^{y} \\ \ln (p) - \ln (p_{0}) & = - \alpha y \\ \ln \left(\dfrac{p}{p_{0}}\right) & = - \alpha y \end{split}\]
This gives the solution
\[p(y) = p_{0} e^{- \alpha y} \ldotp\]
Thus, atmospheric pressure drops exponentially with height, since the y-axis is pointed up from the ground and y has positive values in the atmosphere above sea level. The pressure drops by a factor of \(\frac{1}{e}\) when the height is \(\frac{1}{\alpha}\), which gives us a physical interpretation for \(\alpha\): The constant \(\frac{1}{\alpha}\) is a length scale that characterizes how pressure varies with height and is often referred to as the pressure scale height.
We can obtain an approximate value of \(\alpha\) by using the mass of a nitrogen molecule as a proxy for an air molecule. At temperature 27 °C, or 300 K, we find
\[\alpha = - \frac{mg}{k_{B} T} = \frac{(4.8 \times 10^{-26}\; kg) \times (9.81\; m/s^{2})}{(1.38 \times 10^{-23}\; J/K) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]
Therefore, for every 8800 meters, the air pressure drops by a factor 1/e, or approximately one-third of its value. This gives us only a rough estimate of the actual situation, since we have assumed both a constant temperature and a constant g over such great distances from Earth, neither of which is correct in reality.
Direction of pressure in a fluid
Fluid pressure has no direction, being a scalar quantity, whereas the forces due to pressure have well-defined directions: They are always exerted perpendicular to any surface. The reason is that fluids cannot withstand or exert shearing forces. Thus, in a static fluid enclosed in a tank, the force exerted on the walls of the tank is exerted perpendicular to the inside surface. Likewise, pressure is exerted perpendicular to the surfaces of any object within the fluid. Figure \(\PageIndex{5}\) illustrates the pressure exerted by air on the walls of a tire and by water on the body of a swimmer.