14.2: Fluids, Density, and Pressure (Part 1)
- Page ID
- 4055
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- State the different phases of matter
- Describe the characteristics of the phases of matter at the molecular or atomic level
- Distinguish between compressible and incompressible materials
- Define density and its related SI units
- Compare and contrast the densities of various substances
- Define pressure and its related SI units
- Explain the relationship between pressure and force
- Calculate force given pressure and area
Matter most commonly exists as a solid, liquid, or gas; these states are known as the three common phases of matter. We will look at each of these phases in detail in this section.
Characteristics of Solids
Solids are rigid and have specific shapes and definite volumes. The atoms or molecules in a solid are in close proximity to each other, and there is a significant force between these molecules. Solids will take a form determined by the nature of these forces between the molecules. Although true solids are not incompressible, it nevertheless requires a large force to change the shape of a solid. In some cases, the force between molecules can cause the molecules to organize into a lattice as shown in Figure \(\PageIndex{1}\). The structure of this three-dimensional lattice is represented as molecules connected by rigid bonds (modeled as stiff springs), which allow limited freedom for movement. Even a large force produces only small displacements in the atoms or molecules of the lattice, and the solid maintains its shape. Solids also resist shearing forces. (Shearing forces are forces applied tangentially to a surface, as described in Static Equilibrium and Elasticity.)
Characteristics of Fluids
Liquids and gases are considered to be fluids because they yield to shearing forces, whereas solids resist them. Like solids, the molecules in a liquid are bonded to neighboring molecules, but possess many fewer of these bonds. The molecules in a liquid are not locked in place and can move with respect to each other. The distance between molecules is similar to the distances in a solid, and so liquids have definite volumes, but the shape of a liquid changes, depending on the shape of its container. Gases are not bonded to neighboring atoms and can have large separations between molecules. Gases have neither specific shapes nor definite volumes, since their molecules move to fill the container in which they are held (Figure \(\PageIndex{1}\)).
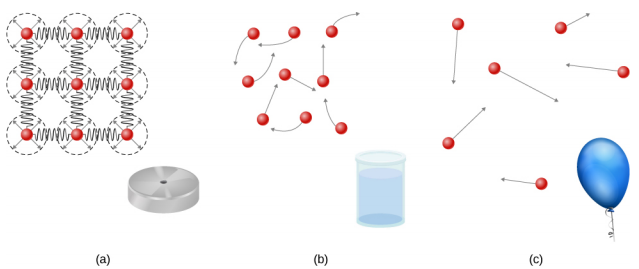
Liquids deform easily when stressed and do not spring back to their original shape once a force is removed. This occurs because the atoms or molecules in a liquid are free to slide about and change neighbors. That is, liquids flow (so they are a type of fluid), with the molecules held together by mutual attraction. When a liquid is placed in a container with no lid, it remains in the container. Because the atoms are closely packed, liquids, like solids, resist compression; an extremely large force is necessary to change the volume of a liquid.
In contrast, atoms in gases are separated by large distances, and the forces between atoms in a gas are therefore very weak, except when the atoms collide with one another. This makes gases relatively easy to compress and allows them to flow (which makes them fluids). When placed in an open container, gases, unlike liquids, will escape.
In this chapter, we generally refer to both gases and liquids simply as fluids, making a distinction between them only when they behave differently. There exists one other phase of matter, plasma, which exists at very high temperatures. At high temperatures, molecules may disassociate into atoms, and atoms disassociate into electrons (with negative charges) and protons (with positive charges), forming a plasma. Plasma will not be discussed in depth in this chapter because plasma has very different properties from the three other common phases of matter, discussed in this chapter, due to the strong electrical forces between the charges.
Density
Suppose a block of brass and a block of wood have exactly the same mass. If both blocks are dropped in a tank of water, why does the wood float and the brass sink (Figure \(\PageIndex{2}\))? This occurs because the brass has a greater density than water, whereas the wood has a lower density than water.
Density is an important characteristic of substances. It is crucial, for example, in determining whether an object sinks or floats in a fluid.
The average density of a substance or object is defined as its mass per unit volume,
\[\rho = \frac{m}{V} \label{14.1}\]
where the Greek letter \(\rho\) (rho) is the symbol for density, m is the mass, and V is the volume.
The SI unit of density is kg/m3. Table 14.1 lists some representative values. The cgs unit of density is the gram per cubic centimeter, g/cm3, where
\[1\; g/cm^{3} = 1000\; kg/m^{3} \ldotp\]
The metric system was originally devised so that water would have a density of 1 g/cm3, equivalent to 103 kg/m3. Thus, the basic mass unit, the kilogram, was first devised to be the mass of 1000 mL of water, which has a volume of 1000 cm3.
Table 14.1 - Densities of Some Common Substances
| Solids | (0.0 °C) | Liquids | (0.0 °C) | Gases | (0.0 °C, 101.3 kPa) |
|---|---|---|---|---|---|
| Substance | \(\rho\)(kg/m3) | Substance | \(\rho\)(kg/m3) | Substance | \(\rho\)(kg/m3) |
| Aluminum | 2.70 x 103 | Benzene | 8.79 x 102 | Air | 1.29 x 100 |
| Bone | 1.90 x 103 | Blood | 1.05 x 103 | Carbon dioxide | .1.98 x 100 |
| Brass | 8.44 x 103 | Ethyl alcohol | 8.06 x 102 | Carbon monoxide | 1.25 x 100 |
| Concrete | 2.40 x 103 | Gasoline | 6.80 x 102 | Helium | 1.80 x 10-1 |
| Copper | 8.92 x 103 | Glycerin | 1.26 x 103 | Hydrogen | 9.00 x 10-2 |
| Cork | 2.40 x 102 | Mercury | 1.36 x 104 | Methane | 7.20 x 10-2 |
| Earth's crust | 3.30 x 103 | Olive oil | 9.20 x 102 | Nitrogen | 1.25 x 100 |
| Glass | 2.60 x 103 | Nitrous oxide | 1.98 x 100 | ||
| Granite | 2.70 x 103 | Oxygen | 1.43 x 100 | ||
| Iron | 7.86 x 103 | ||||
| Lead | 1.13 x 104 | ||||
| Oak | 7.10 x 102 | ||||
| Pine | 3.73 x 102 | ||||
| Platinum | 2.14 x 104 | ||||
| Polystyrene | 1.00 x 102 | ||||
| Tungsten | 1.93 x 104 | ||||
| Uranium | 1.87 x 103 |
As you can see by examining Table 14.1, the density of an object may help identify its composition. The density of gold, for example, is about 2.5 times the density of iron, which is about 2.5 times the density of aluminum. Density also reveals something about the phase of the matter and its substructure. Notice that the densities of liquids and solids are roughly comparable, consistent with the fact that their atoms are in close contact. The densities of gases are much less than those of liquids and solids, because the atoms in gases are separated by large amounts of empty space. The gases are displayed for a standard temperature of 0.0 °C and a standard pressure of 101.3 kPa, and there is a strong dependence of the densities on temperature and pressure. The densities of the solids and liquids displayed are given for the standard temperature of 0.0 °C and the densities of solids and liquids depend on the temperature. The density of solids and liquids normally increase with decreasing temperature.
Table 14.2 shows the density of water in various phases and temperature. The density of water increases with decreasing temperature, reaching a maximum at 4.0 °C, and then decreases as the temperature falls below 4.0 °C. This behavior of the density of water explains why ice forms at the top of a body of water.
Table 14.2 - Densities of Water
| Substance | \(\rho\)(kg/m3) |
|---|---|
| Ice (0 °C) | 9.17 x 102 |
| Water (0 °C) | 9.998 x 102 |
| Water (4 °C) | 1.000 x 103 |
| Water (20 °C) | 9.982 x 102 |
| Water (100 °C) | 9.584 x 102 |
| Steam (100 °C, 101.3 kPa) | 1.670 x 102 |
| Sea water (0°C) | 1.030 x 103 |
The density of a substance is not necessarily constant throughout the volume of a substance. If the density is constant throughout a substance, the substance is said to be a homogeneous substance. A solid iron bar is an example of a homogeneous substance. The density is constant throughout, and the density of any sample of the substance is the same as its average density. If the density of a substance were not constant, the substance is said to be a heterogeneous substance. A chunk of Swiss cheese is an example of a heterogeneous material containing both the solid cheese and gas-filled voids. The density at a specific location within a heterogeneous material is called local density, and is given as a function of location, \(\rho\) = \(\rho\)(x, y, z) (Figure \(\PageIndex{3}\)).
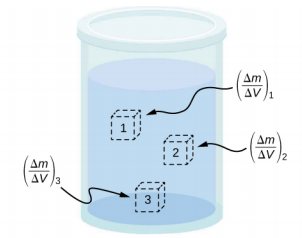
Local density can be obtained by a limiting process, based on the average density in a small volume around the point in question, taking the limit where the size of the volume approaches zero,
\[\rho = \lim_{\Delta V \rightarrow 0} \frac{\Delta m}{\Delta V} \label{14.2}\]
where \(\rho\) is the density, m is the mass, and V is the volume.
Since gases are free to expand and contract, the densities of the gases vary considerably with temperature, whereas the densities of liquids vary little with temperature. Therefore, the densities of liquids are often treated as constant, with the density equal to the average density.
Density is a dimensional property; therefore, when comparing the densities of two substances, the units must be taken into consideration. For this reason, a more convenient, dimensionless quantity called the specific gravity is often used to compare densities. Specific gravity is defined as the ratio of the density of the material to the density of water at 4.0 °C and one atmosphere of pressure, which is 1000 kg/m3:
\[Specific\; gravity = \frac{Density\; of\; material}{Density\; of\; water} \ldotp\]
The comparison uses water because the density of water is 1 g/cm3, which was originally used to define the kilogram. Specific gravity, being dimensionless, provides a ready comparison among materials without having to worry about the unit of density. For instance, the density of aluminum is 2.7 in g/cm3 (2700 in kg/m3), but its specific gravity is 2.7, regardless of the unit of density. Specific gravity is a particularly useful quantity with regard to buoyancy, which we will discuss later in this chapter.
Pressure
You have no doubt heard the word ‘pressure’ used in relation to blood (high or low blood pressure) and in relation to weather (high- and low-pressure weather systems). These are only two of many examples of pressure in fluids. (Recall that we introduced the idea of pressure in Static Equilibrium and Elasticity, in the context of bulk stress and strain.)
Pressure (p) is defined as the normal force F per unit area A over which the force is applied, or
\[p = \frac{F}{A} \ldotp \label{14.3}\]
To define the pressure at a specific point, the pressure is defined as the force dF exerted by a fluid over an infinitesimal element of area dA containing the point, resulting in p = \(\frac{dF}{dA}\).
A given force can have a significantly different effect, depending on the area over which the force is exerted. For instance, a force applied to an area of 1 mm2 has a pressure that is 100 times as great as the same force applied to an area of 1 cm2 . That is why a sharp needle is able to poke through skin when a small force is exerted, but applying the same force with a finger does not puncture the skin (Figure \(\PageIndex{4}\)).
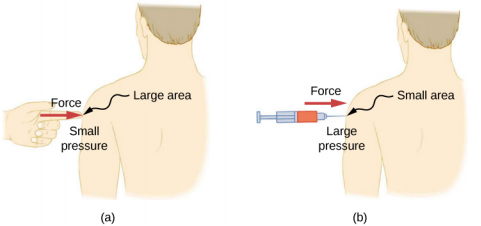
Note that although force is a vector, pressure is a scalar. Pressure is a scalar quantity because it is defined to be proportional to the magnitude of the force acting perpendicular to the surface area. The SI unit for pressure is the pascal (Pa), named after the French mathematician and physicist Blaise Pascal (1623–1662), where
\[1\; Pa = 1\; N/m^{2} \ldotp\]
Several other units are used for pressure, which we discuss later in the chapter.