17.9: Shock Waves
- Page ID
- 4737
- Explain the mechanism behind sonic booms
- Describe the difference between sonic booms and shock waves
- Describe a bow wake
When discussing the Doppler effect of a moving source and a stationary observer, the only cases we considered were cases where the source was moving at speeds that were less than the speed of sound. Recall that the observed frequency for a moving source approaching a stationary observer is fo = fs\(\left(\dfrac{v}{v - v_{s}}\right)\). As the source approaches the speed of sound, the observed frequency increases. According to the equation, if the source moves at the speed of sound, the denominator is equal to zero, implying the observed frequency is infinite. If the source moves at speeds greater than the speed of sound, the observed frequency is negative.
What could this mean? What happens when a source approaches the speed of sound? It was once argued by some scientists that such a large pressure wave would result from the constructive interference of the sound waves, that it would be impossible for a plane to exceed the speed of sound because the pressures would be great enough to destroy the airplane. But now planes routinely fly faster than the speed of sound. On July 28, 1976, Captain Eldon W. Joersz and Major George T. Morgan flew a Lockheed SR-71 Blackbird #61-7958 at 3529.60 km/h (2193.20 mi/h), which is Mach 2.85. The Mach number is the speed of the source divided by the speed of sound:
\[M = \frac{v_{s}}{v} \ldotp \label{17.21}\]
You will see that interesting phenomena occur when a source approaches and exceeds the speed of sound.
Doppler Effect and High Velocity
What happens to the sound produced by a moving source, such as a jet airplane, that approaches or even exceeds the speed of sound? The answer to this question applies not only to sound but to all other waves as well. Suppose a jet plane is coming nearly straight at you, emitting a sound of frequency fs. The greater the plane’s speed vs, the greater the Doppler shift and the greater the value observed for fo (Figure \(\PageIndex{1}\)).
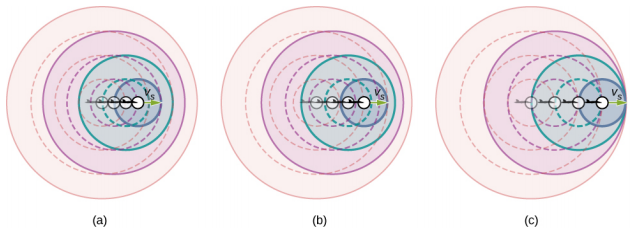
Now, as vs approaches the speed of sound, fo approaches infinity, because the denominator in fo = fs \(\left(\dfrac{v}{v \mp v_{s}}\right)\) approaches zero. At the speed of sound, this result means that in front of the source, each successive wave interferes with the previous one because the source moves forward at the speed of sound. The observer gets them all at the same instant, so the frequency is infinite [part (c) of the figure].
Shock Waves and Sonic Booms
If the source exceeds the speed of sound, no sound is received by the observer until the source has passed, so that the sounds from the approaching source are mixed with those from it when receding. This mixing appears messy, but something interesting happens—a shock wave is created (Figure \(\PageIndex{2}\)).
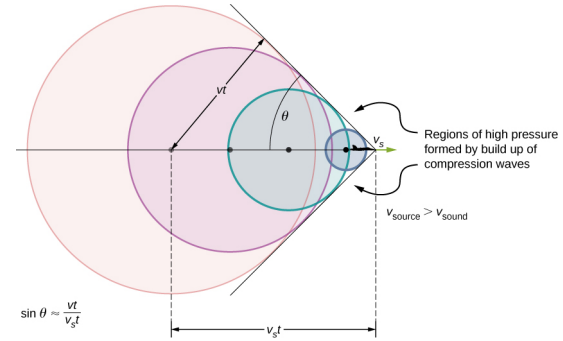
Constructive interference along the lines shown (a cone in three dimensions) from similar sound waves arriving there simultaneously. This superposition forms a disturbance called a shock wave, a constructive interference of sound created by an object moving faster than sound. Inside the cone, the interference is mostly destructive, so the sound intensity there is much less than on the shock wave. The angle of the shock wave can be found from the geometry. In time t the source has moved vst and the sound wave has moved a distance vt and the angle can be found using sin \(\theta\) = \(\frac{vt}{v_{s} t} = \frac{v}{v_{s}}\). Note that the Mach number is defined as \(\frac{v_{s}}{v}\) so the sine of the angle equals the inverse of the Mach number,
\[\sin \theta = \frac{v}{w_{s}} = \frac{1}{M} \ldotp \label{17.22}\]
You may have heard of the common term ‘sonic boom.’ A common misconception is that the sonic boom occurs as the plane breaks the sound barrier; that is, accelerates to a speed higher than the speed of sound. Actually, the sonic boom occurs as the shock wave sweeps along the ground.
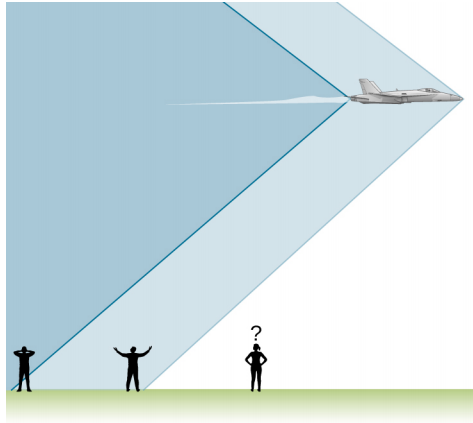
An aircraft creates two shock waves, one from its nose and one from its tail (Figure \(\PageIndex{3}\)). During television coverage of space shuttle landings, two distinct booms could often be heard. These were separated by exactly the time it would take the shuttle to pass by a point. Observers on the ground often do not see the aircraft creating the sonic boom, because it has passed by before the shock wave reaches them, as seen in the figure. If the aircraft flies close by at low altitude, pressures in the sonic boom can be destructive and break windows as well as rattle nerves. Because of how destructive sonic booms can be, supersonic flights are banned over populated areas.
Shock waves are one example of a broader phenomenon called bow wakes. A bow wake, such as the one in Figure \(\PageIndex{4}\), is created when the wave source moves faster than the wave propagation speed. Water waves spread out in circles from the point where created, and the bow wake is the familiar V-shaped wake, trailing the source. A more exotic bow wake is created when a subatomic particle travels through a medium faster than the speed of light travels in that medium. (In a vacuum, the maximum speed of light is c = 3.00 × 108 m/s; in the medium of water, the speed of light is closer to 0.75c.) If the particle creates light in its passage, that light spreads on a cone with an angle indicative of the speed of the particle, as illustrated in Figure \(\PageIndex{5}\). Such a bow wake is called Cerenkov radiation and is commonly observed in particle physics.




