18.16: Waves
( \newcommand{\kernel}{\mathrm{null}\,}\)
$Check Your Understanding
16.1. The wavelength of the waves depends on the frequency and the velocity of the wave. The frequency of the sound wave is equal to the frequency of the wave on the string. The wavelengths of the sound waves and the waves on the string are equal only if the velocities of the waves are the same, which is not always the case. If the speed of the sound wave is different from the speed of the wave on the string, the wavelengths are different. This velocity of sound waves will be discussed in Sound.
16.2. In a transverse wave, the wave may move at a constant propagation velocity through the medium, but the medium oscillates perpendicular to the motion of the wave. If the wave moves in the positive x-direction, the medium oscillates up and down in the y-direction. The velocity of the medium is therefore not constant, but the medium’s velocity and acceleration are similar to that of the simple harmonic motion of a mass on a spring.
16.3. Yes, a cosine function is equal to a sine function with a phase shift, and either function can be used in a wave function. Which function is more convenient to use depends on the initial conditions. In Figure 16.11, the wave has an initial height of y(0.00, 0.00) = 0 and then the wave height increases to the maximum height at the crest. If the initial height at the initial time was equal to the amplitude of the wave y(0.00, 0.00) = +A, then it might be more convenient to model the wave with a cosine function.
16.4. This wave, with amplitude A = 0.5 m, wavelength λ = 10.00 m, period T = 0.50 s, is a solution to the wave equation with a wave velocity v = 20.00 m/s.
16.5. Since the speed of a wave on a taunt string is proportional to the square root of the tension divided by the linear density, the wave speed would increase by √2.
16.6. At first glance, the time-averaged power of a sinusoidal wave on a string may look proportional to the linear density of the string because P = 12μA2ω2v; however, the speed of the wave depends on the linear density. Replacing the wave speed with √FTμ shows that the power is proportional to the square root of tension and proportional to the square root of the linear mass density: P=12μA2ω2v=12μA2ω2√FTμ=12A2ω2√μFT.
16.7. Yes, the equations would work equally well for symmetric boundary conditions of a medium free to oscillate on each end where there was an antinode on each end. The normal modes of the first three modes are shown below. The dotted line shows the equilibrium position of the medium.
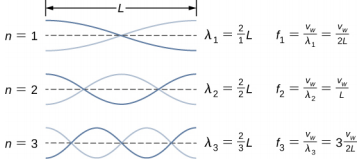
Note that the first mode is two quarters, or one half, of a wavelength. The second mode is one quarter of a wavelength, followed by one half of a wavelength, followed by one quarter of a wavelength, or one full wavelength. The third mode is one and a half wavelengths. These are the same result as the string with a node on each end. The equations for symmetrical boundary conditions work equally well for fixed boundary conditions and free boundary conditions. These results will be revisited in the next chapter when discussing sound wave in an open tube.
Conceptual Questions
1. A wave on a guitar string is an example of a transverse wave. The disturbance of the string moves perpendicular to the propagation of the wave. The sound produced by the string is a longitudinal wave where the disturbance of the air moves parallel to the propagation of the wave.
3. Propagation speed is the speed of the wave propagating through the medium. If the wave speed is constant, the speed can be found by v = λT = λf. The frequency is the number of wave that pass a point per unit time. The wavelength is directly proportional to the wave speed and inversely proportional to the frequency.
5. No, the distance you move your hand up and down will determine the amplitude of the wave. The wavelength will depend on the frequency you move your hand up and down, and the speed of the wave through the spring.
7. Light from the Sun and stars reach Earth through empty space where there is no medium present.
9. The wavelength is equal to the velocity of the wave times the frequency and the wave number is equal to k = 2πλ, so yes, the wave number will depend on the frequency and also depend on the velocity of the wave propagating through the spring.
11. The medium moves in simple harmonic motion as the wave propagates through the medium, continuously changing speed, therefore it accelerates. The acceleration of the medium is due to the restoring force of the medium, which acts in the opposite direction of the displacement.
13. The wave speed is proportional to the square root of the tension, so the speed is doubled.
15. Since the speed of a wave on a string is inversely proportional to the square root of the linear mass density, the speed would be higher in the low linear mass density of the string.
17. The tension in the wire is due to the weight of the electrical power cable.
19. The time averaged power is P = EλT = 12μA2ω2λT=12μA2ω2v. If the frequency or amplitude is halved, the power decreases by a factor of 4.
21. As a portion on the string moves vertically, it exerts a force on the neighboring portion of the string, doing work on the portion and transferring the energy.
23. The intensity of a spherical wave is I = P4πr2, if no energy is dissipated the intensity will decrease by a factor of nine at three meters.
25. At the interface, the incident pulse produces a reflected pulse and a transmitted pulse. The reflected pulse would be out of phase with respect to the incident pulse, and would move at the same propagation speed as the incident pulse, but would move in the opposite direction. The transmitted pulse would travel in the same direction as the incident pulse, but at half the speed. The transmitted pulse would be in phase with the incident pulse. Both the reflected pulse and the transmitted pulse would have amplitudes less than the amplitude of the incident pulse.
27.
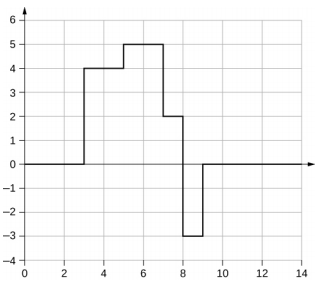
29. It may be as easy as changing the length and/or the density a small amount so that the parts do not resonate at the frequency of the motor.
31. Energy is supplied to the glass by the work done by the force of your finger on the glass. When supplied at the right frequency, standing waves form. The glass resonates and the vibrations produce sound.
33. For the equation y(x, t) = 4.00 cm sin(3 m−1 x)cos(4 s−1 t), there is a node because when x = 0.00 m , sin(3 m−1 (0.00 m)) = 0.00, so y(0.00 m, t) = 0.00 m for all time. For the equation y(x, t) = 4.00 cm sin(3 m−1 x + π2)cos(4 s−1 t), there is an antinode because when x = 0.00 m, sin(3 m−1 (0.00 m) + π2) = + 1.00, so y(0.00 m, t) oscillates between +A and −A as the cosine term oscillates between +1 and -1.
Problems
35. 2d = vt ⇒ d = 11.25 m
37. v = fλ, so that f = 0.125 Hz, so that N = 7.50 times
39. v = fλ⇒λ = 0.400 m
41. v = fλ⇒ f = 2.50 x 109 Hz
43. a. The P-waves outrun the S-waves by a speed of v = 3.20 km/s; therefore, Δd = 0.320 km.
b. Since the uncertainty in the distance is less than a kilometer, our answer to part (a) does not seem to limit the detection of nuclear bomb detonations. However, if the velocities are uncertain, then the uncertainty in the distance would increase and could then make it difficult to identify the source of the seismic waves.
45. v = 1900 m/s, Δt = 1.05 μs
47. y(x, t) = −0.037 cm
49. The pulse will move Δx = 6.00 m.
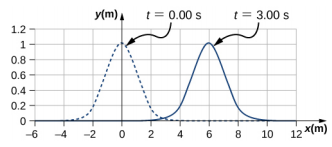
51. a. A = 0.25 m
b. k = 0.30 m−1
c. ω = 0.90 s−1
d. v = 3.0 m/s
e. ϕ = π3 rad
f. λ = 20.93 m
g. T = 6.98 s
53. A = 0.30 m, λ = 4.50 m, v = 18.00 m/s, f = 4.00 Hz, T = 0.25 s
55. y(x, t) = 0.23 m sin(3.49 m−1 x − 0.63 s−1 t)
57. They have the same angular frequency, frequency, and period. They are traveling in opposite directions and y2(x, t) has twice the wavelength as y1(x, t) and is moving at half the wave speed.
59. Each particle of the medium moves a distance of 4A each period. The period can be found by dividing the velocity by the wavelength: t = 10.42 s
61. a. μ = 0.040 kg/m
b. v = 15.75 m/s
63. v = 180 m/s
65. v = 547.723 m/s, Δt = 5.48 ms
67. vs = 347.56 m/s
69. v1t + v2t = 2.00 m, t = 1.69 ms
71. v = 288.68 m/s, λ = 0.73 m
73. a. A = 0.0125 cm
b. FT = 0.96 N
75. v = 74.54 m/s, Pλ = 91.85 W
77. I = 20.0 W/m2
b. I = PA, A = 10.0 m2 A = 4πr2, r = 0.892 m
79. I = 650 W/m2
81. P∝E∝I∝X2⇒P2P1=(X2X1)2
P2 = 2.50 kW
83. I∝X2⇒I1I2=(X1X2)2
I2 = 3.38 x 10−5 W/m2
85. f = 100.00 Hz, A = 1.10 cm
87. a. I2 = 0.063I1
b. I1 4πr12 = I24πr22, r2 = 3.16 m
89. 2πr1A12 = 2πr2A22, A1 = (r2r1)1/2, A1 = 0.17 m
91. y(x, t) = 0.76 m
93. AR = 2A cos(ϕ2), ϕ = 1.17 rad
95. yR = 1.90 cm
97. ω = 6.28 s−1, k = 3.00 m−1, ϕ = π8 rad, AR = 2A cos (ϕ2), A = 0.37 m
99. a.
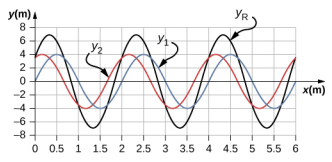
b. λ = 2.0 m, A = 4 m
c. λR = 2.0 m, AR = 6.93 m
101. yR (x, t) = 2A cos (ϕ2)cos(kx−ωt+ϕ2); The result is not surprising because cos(θ) = sin(θ+π2).
103. λn=2.00nL,fn=vλnλ1=4.00m,f1=12.5Hzλ2=2.00m,f2=25.00Hzλ3=1.33m,f3=37.59Hz
105. v = 158.11 m/s, λ= 4.44 m, f = 35.61 Hz, λs = 9.63 m
107. y(x, t) = [0.60 cm sin(3 m−1 x)]cos(4 s−1 t)
109. λ100=0.06mv=56.8m/s,fn=nf1,n=1,2,3,4,5…f100=947Hz
111. T = 2Δt, v = λT, λ = 2.12 m
113. λ1 = 6.00 m, λ2 = 3.00 m, λ3 = 2.00 m, λ4 = 1.50 m; v = 258.20 m/s = λf; f1 = 43.03 Hz, f2 = 86.07 Hz, f3 = 129.10 Hz, f4 = 172.13 Hz
115. v = 134.16 ms, λ = 1.4 m, f = 95.83 Hz, T = 0.0104 s
Additional Problems
117. λ = 0.10 m
119. a. f = 4.74 x 1014 Hz
b. λ = 422 nm
121. λ = 16.00 m, f = 0.10 Hz, T = 10.00 s, v = 1.6 m/s
123. λ = (vb + v)tb, v = 3.75 m/s, λ = 3.00 m
125. ∂2(y1+y2)∂t2=−Aω2sin(kx−ωt)−Aω2sin(kx−ωt+ϕ)∂2(y1+y2)∂x2=−Ak2sin(kx−ωt)−Ak2sin(kx−ωt+ϕ)∂2y(x,t)∂x2=1v2∂2y(x,t)∂t2−Aω2sin(kx−ωt)−Aω2sin(kx−ωt+ϕ)=(1v2)(−Ak2sin(kx−ωt)−Ak2sin(kx−ωt+ϕ))v=ωk
127. y(x, t) = 0.40 m sin(0.015 m−1 x + 1.5 s−1 t)
129. v = 223.61 m/s, k = 1.57 m−1, ω = 142.43 s−1
131. P = 12A2(2πf)2√μFT, μ = 2.00 x 10−4 kg/m
133. P = 12μA2ω2λT, μ = 0.0018 kg/m
135. a. AR = 2A cos(ϕ2), cos(ϕ2) = 1, ϕ = 0, 2π, 4π, ...
b. AR = 2A cos(ϕ2), cos(ϕ2) = 0, ϕ = 0, π, 3π, 5\(\pi), ...
137. yR(x, t) = 0.6 m sin(4 m−1)cos(3 s−1 t)
139. a. FT−20.00kg(9.80m/s2)cos45o=0m(9.80m/s2)−FT=0m=14.14kg
b. FT = 138.57 N, v = 74.45 m/s
141. FT = 2 N, v = 6.73 m/s
143. a. fn = nv2L, v = 2Lfn+1n+1, n+1n=2Lfn+12Lfn, 1 + 1n = 1.2, n = 5; λn = 2nL, λ5 = 1.6 m, λ6 = 1.33 m
b. FT = 245.76 N
Challenge Problems
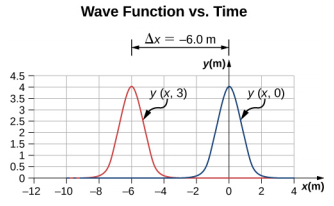
145. a. Moves in the negative x direction at a propagation speed of v = 2.00 m/s.
b. Δx = −6.00 m
c.
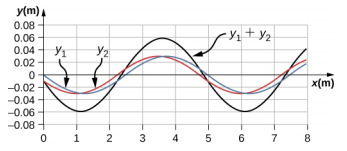
147. sin(kx−ωt)=sin(kx+ϕ2)cos(ωt+ϕ2)−cos(kx+ϕ2)sin(ωt+ϕ2)sin(kx−ωt+ϕ)=sin(kx+ϕ2)cos(ωt+ϕ2)+cos(kx+ϕ2)sin(ωt+ϕ2)sin(kx−ωt)+sin(kx−ωt+ϕ)=2sin(kx+ϕ2)cos(ωt+ϕ2)yR=2Asin(kx+ϕ2)cos(ωt+ϕ2)
149. sin(kx+ϕ2) = 0, kx + ϕ2 = 0, π, 2π, 1.26 m−1 x + π20 = π, 2π, 3π; x = 2.37 m, 4.86 m, 7.35 m
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


