18.3: Motion Along a Straight Line
( \newcommand{\kernel}{\mathrm{null}\,}\)
Check Your Understanding
3.1. (a) The rider’s displacement is \Deltax = xf − x0 = −1 km. (The displacement is negative because we take east to be positive and west to be negative.) (b) The distance traveled is 3 km + 2 km = 5 km. (c) The magnitude of the displacement is 1 km.
3.2. (a) Taking the derivative of x(t) gives v(t) = −6t m/s. (b) No, because time can never be negative. (c) The velocity is v(1.0 s) = −6 m/s and the speed is |v(1.0 s)| = 6 m/s.
3.3. Inserting the knowns, we have \bar{a} = \frac{\Delta v}{\Delta t} = \frac{2.0 \times 10^{7}\; m/s − 0}{10^{−4}\; s − 0} = 2.0 \times 10^{11}\; m/s^{2}.
3.4. If we take east to be positive, then the airplane has negative acceleration because it is accelerating toward the west. It is also decelerating; its acceleration is opposite in direction to its velocity.
3.5. To answer this, choose an equation that allows us to solve for time t, given only a , v0, and vv = v_{0} + at \ldotp Rearrange to solve for t:$$t = \frac{v − v_{0}}{a} = \frac{400\; m/s − 0\; m/s}{20\; m/s^{2}} = 20 s \ldotp\]
3.6. a = \frac{2}{3} m/s2.
3.7. It takes 2.47 s to hit the water. The quantity distance traveled increases faster.
3.8. a. The velocity function is the integral of the acceleration function plus a constant of integration. By Equation 3.91,v(t) = \int a(t)dt + C_{1} = \int (5 − 10t)dt + C_{1} = 5t − 5t^{2} + C_{1} \ldotp Since v(0) = 0, we have C1 = 0; so,v(t) = 5t − 5t^{2} \ldotp b. By Equation 3.93,x(t) = \int v(t)dt + C_{2} = \int (5t − 5t^{2})dt + C_{2} = \frac{5}{2} t^{2} − \frac{5}{3} t^{3} + C_{2} \ldotp Since x(0) = 0, we have C2 = 0, andx(t) = \frac{5}{2} t^{2} − \frac{5}{3} t^{3} \ldotp c. The velocity can be written as v(t) = 5t(1 – t), which equals zero at t = 0, and t = 1 s.
Conceptual Questions
1. You drive your car into town and return to drive past your house to a friend’s house.
3. If the bacteria are moving back and forth, then the displacements are canceling each other and the final displacement is small.
5. Distance traveled
7. Average speed is the total distance traveled divided by the elapsed time. If you go for a walk, leaving and returning to your home, your average speed is a positive number. Since Average velocity = Displacement/Elapsed time, your average velocity is zero.
9. Average speed. They are the same if the car doesn’t reverse direction.
11. No, in one dimension constant speed requires zero acceleration.
13. A ball is thrown into the air and its velocity is zero at the apex of the throw, but acceleration is not zero.
15. Plus, minus
17. If the acceleration, time, and displacement are the knowns, and the initial and final velocities are the unknowns, then two kinematic equations must be solved simultaneously. Also if the final velocity, time, and displacement are the knowns then two kinematic equations must be solved for the initial velocity and acceleration.
19. a. At the top of its trajectory; b. yes, at the top of its trajectory; c. yes
21. Earthv = v_{0} − gt = −gt; Moonv′ = \frac{g}{6} t′ v = v′ − gt = − \frac{g}{6}t′ t′ = 6t; Earth y = − \frac{1}{2}gt^{2} Moon $$y′ = − \frac{1}{2} \frac{g}{6} (6t)^{2} = − \frac{1}{2} g6t^{2} = −6 \left(\dfrac{1}{2} gt^{2}\right) = −6y\]
Problems
25. a. \vec{x}_{1} = (−2.0 m) \hat{i}, \vec{x}_{2} = (5.0 m) \hat{i}
b. 7.0 m east
27. a. t = 2.0 s
b. x(6.0) − x(3.0) = −8.0 − (−2.0) = −6.0 m
29. a. 150.0 s, \vec{v} = 156.7 m/s
b. 45.7% the speed of sound at sea level
31.
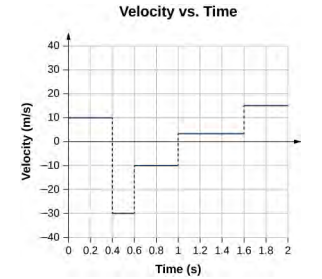
33.
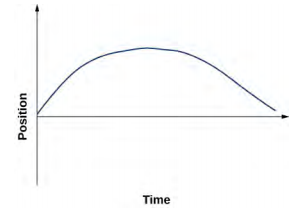
35. a. v(t) = (10 − 4t)m/s; v(2 s) = 2 m/s, v(3 s) = −2 m/s
b. |v(2 s)| = 2 m/s, |v(3 s)| = 2 m/s
c. \bar{v} = 0 m/s
37. a = 4.29 m/s2
39.
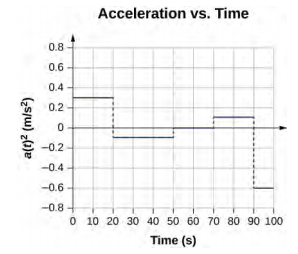
41. a = 11.1g
43. 150 m
45. a. 525 m
b. v = 180 m/s
47. a.
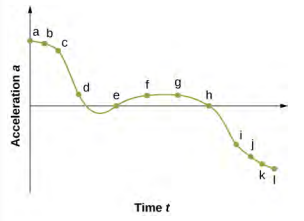
b. The acceleration has the greatest positive value at ta c. The acceleration is zero at te and th d. The acceleration is negative at ti, tj, tk, tl
49. a. a = −1.3 m/s2
b. v0 = 18 m/s
c. t = 13.8 s
51. v = 502.20 m/s
53. a.

b. Knowns: a = 2.40 m/s2, t = 12.0 s, v0 = 0 m/s , and x0 = 0 m; c. x = x0 + v0t + \frac{1}{2}at2 = \frac{1}{2}at2 = 2.40 m/s2 (12.0 s)2 = 172.80 m, the answer seems reasonable at about 172.8 m; d. v = 28.8 m/s
55. a.

b. Knowns: v = 30.0 cm/s, x = 1.80 cm
c. a = 250 cm/s2, t = 0.12 s
d. yes
57. a. 6.87 m/s2
b. x = 52.26 m
59. a. a = 8450 m/s2
b. t = 0.0077 s
61. a. a = 9.18g
b. t = 6.67 x 10−3 s
c. a = −40.0 m/s2, a = 4.08g
63. Knowns: x = 3 m, v = 0 m/s, v0 = 54 m/s. We want a, so we can use this equation: a = −486 m/s2.
65. a. a = 32.58 m/s2
b. v = 161.85 m/s
c. v > vmax, because the assumption of constant acceleration is not valid for a dragster. A dragster changes gears and would have a greater acceleration in first gear than second gear than third gear, and so on. The acceleration would be greatest at the beginning, so it would not be accelerating at 32.6 m/s2 during the last few meters, but substantially less, and the final velocity would be less than 162 m/s.
67. a. y = −8.23 m, v1 = −18.9 m/s
b. y = −18.9 m, v2 = 23.8 m/s
c. y = −32.0 m, v3 = −28.7 m/s
d. y = −47.6 m, v4 = −33.6 m/s
e. y = −65.6 m, v5 = −38.5 m/s
69. a. Knowns: a = −9.8 m/s2, v0 = −1.4 m/s, t = 1.8 s, y0 = 0 m
b. y = y0 + v0t − \frac{1}{2}gt2, y = v0t − \frac{1}{2}gt = −1.4 m/s (1.8 sec) − \frac{1}{2}(9.8)(1.8 s)2 = −18.4 m and the origin is at the rescuers, who are 18.4 m above the water.
71. a. v2 = v02 − 2g(y − y0), y0 = 0, v = 0, y = \frac{v_{0}^{2}}{2g} = \frac{(4.0 m/s)^{2}}{2(9.80)} = 0.82 m
b. To the apex v = 0.41 s times 2 to the board = 0.82 s from the board to the water y = y0 + v0t − \frac{1}{2}gt2, y = −1.80 m, y0 = 0, v0 = 4.0 m/s −1.8 = 4.0t − 4.9t2, 4.9t 2 − 4.0t − 1.80 = 0, solution to quadratic equation gives 1.13 s
c. v2 = v02 − 2g(y − y0)y0 = 0, v0 = 4.0 m/s, y = −1.80 m, v = 7.16 m/s
73. Time to the apex: t = 1.12 s times 2 equals 2.24 s to a height of 2.20 m. To 1.80 m in height is an additional 0.40 m.y = y_{0} + v_{0} t − \frac{1}{2} gt^{2}y = −0.40\; my_{0} = 0v_{0} = −11.0\; m/s−0.40 = −11.0t − 4.9t^{2}\; or\; 4.9t^{2} + 11.0t − 0.40 = 0 \ldotp Take the positive root, so the time to go the additional 0.4 m is 0.04 s. Total time is 2.24 s + 0.04 s = 2.28 s.
75. a. v2 = v02 − 2g(y − y0), y0 = 0, v = 0, y = 2.50 m,$$v_{0}^{2} = 2gy \Rightarrow v_{0} = \sqrt{2(9.80)(2.50)} = 7.0\; m/s;\]
b. t = 0.72 s times 2 gives 1.44 s in the air
77. a. v = 70.0 m/s
b. time heard after rock begins to fall: 0.75 s, time to reach the ground: 6.09 s
79. a. A = m/s2, B = m/s5/2
b. v(t) = \int a(t)dt + C1 = \int(A − Bt1/2)dt + C1 = At − \frac{2}{3}Bt3/2 + C1v(0) = 0 = C_{1}\; so\; v(t_{0}) = At_{0} − \frac{2}{3} Bt_{0}^{3/2};
c. x(t) = \intv(t)dt + C2 = \int(At − \frac{2}{3}\)Bt3/2)dt + C2 = \frac{1}{2}At2 − \frac{4}{15}Bt5/2 + C2x(0) = 0 = C_{2}\; so\; x(t_{0}) = \frac{1}{2} At_{0}^{2} − \frac{4}{15} Bt_{0}^{5/2}
81. a. $$\begin{split}a(t) & = 3.2 m/s^{2} \quad t \leq 5.0\; s \\ a(t) & = 1.5\; m/s^{2} \quad 5.0\; s \leq t \leq 11.0\; s \\ a(t) & = 0\; m/s^{2} \quad \quad t > 11.0\; s \end{split}\]
b. \begin{split} x(t) & = \int v(t)dt + C_{2} = \int 3.2tdt + C_{2} = 1.6t^{2} + C_{2} \quad t \leq 5.0\; s \\ x(0) & = 0 \Rightarrow C_{2} = 0\; therefore,\; x(2.0\; s) = 6.4\; m \\ x(t) & = \int v(t)dt + C_{2} = \int [16.0 − 1.5(t − 5.0)]dt + C_{2} = 16t − 1.5 \left(\dfrac{t^{2}}{2} − 5.0t \right) + C_{2} \quad 5.0\; s \leq t \leq 11.0\; s \\ x(5\; s) & = 1.6(5.0)^{2} = 40\; m = 16(5.0\; s) − 1.5 \left(\dfrac{5^{2}}{2} − 5.0(5.0) \right) + C_{2} \end{split}$$\begin{split}40 & = 98.75 + C_{2} \Rightarrow C_{2} = −58.75 \\ x(7.0 s) & = 16(7.0) − 1.5 \left(\dfrac{7^{2}}{2} − 5.0(7) \right) − 58.75 = 69\; m \\ x(t) & = \int 7.0dt + C_{2} = 7t + C_{2} \quad t \geq 11.0\; s \\ x(11.0\; s) & = 16(11) − 1.5 \left(\dfrac{11^{2}}{2} − 5.0(11) \right) − 58.75 = 109 = 7(11.0\; s) + C_{2} \Rightarrow C_{2} = 32\; m \\ x(t) & = 7t + 32\; m \quad x \geq 11.0\; s \Rightarrow x(12.0\; s) = 7(12) + 32 = 116\; m \end{split}\]
Additional Problems
83. Take west to be the positive direction. 1st plane: \bar{v} = 600 km/h; 2nd plane: \bar{v} = 667.0 km/h
85. a = \frac{v − v_{0}}{t − t_{0}}, t = 0, a = \frac{−3.4\; cm/s − v_{0}}{4\; s} = 1.2 cm/s2 \Rightarrow v0 = − 8.2 cm/s, v = v0 + at = − 8.2 + 1.2 t; v = −7.0 cm/s, v = −1.0 cm/s
87. a = −3 m/s2
89. a. v = 8.7 x 105 m/s
b. t = 7.8 x 10−8 s
91. 1 km = v0(80.0 s) + \frac{1}{2}a(80.0)2; 2 km = v0(200.0) + \frac{1}{2}a(200.0)2 solve simultaneously to get a = − \frac{0.1}{2400.0}km/s2 and v0 = 0.014167 km/s, which is 51.0 km/h. Velocity at the end of the trip is v = 21.0 km/h.
93. a = −0.9 m/s2
95. Equation for the speeding car: This car has a constant velocity, which is the average velocity, and is not accelerating, so use the equation for displacement with x0 = 0: x = x0 + \bar{v}t = \bar{v}t; Equation for the police car: This car is accelerating, so use the equation for displacement with x0 = 0 and v0 = 0, since the police car starts from rest: x = x0 + v0t + \frac{1}{2}at2 = \frac{1}{2}at2; Now we have an equation of motion for each car with a common parameter, which can be eliminated to find the solution. In this case, we solve for t. Step 1, eliminating x : x = \bar{v}t = \frac{1}{2}at2; Step 2, solving for t : t = \frac{2 \bar{v}}{a}. The speeding car has a constant velocity of 40 m/s, which is its average velocity. The acceleration of the police car is 4 m/s2. Evaluating t, the time for the police car to reach the speeding car, we have t = \frac{2 \bar{v}}{a} = \frac{2(40)}{4} = 20 s.
97. At this acceleration she comes to a full stop in t = \frac{−v_{0}}{a} = \frac{8}{0.5} = 16 s, but the distance covered is x = 8 m/s (16 s) − \frac{1}{2}(0.5)(16 s)2 = 64 m, which is less than the distance she is away from the finish line, so she never finishes the race.
99. x1 = \frac{3}{2}v0t; x2 = \frac{5}{3}x1
101. v0 = 7.9 m/s velocity at the bottom of the window. v = 7.9 m/s; v0 = 14.1 m/s
103. a. v = 5.42 m/s
b. v = 4.64 m/s
c. a = 2874.28 m/s2
d. (x − x0) = 5.11 x 10−3 m
105. Consider the players fall from rest at the height 1.0 m and 0.3 m. 0.9 s; 0.5 s
107. a. t = 6.37 s taking the positive root
b. v = 59.5 m/s
109. a. y = 4.9 m
b. v = 38.3 m/s; c. −33.3 m
111. h = \frac{1}{2}gt2, h = total height and time to drop to ground \frac{2}{3}h = \frac{1}{2}g(t − 1)2 in t – 1 seconds it drops \frac{2}{3}h\frac{2}{3} \left(\dfrac{1}{2} gt^{2}\right) = \frac{1}{2} g(t − 1)^{2}\; or\; \frac{t^{2}}{3} = \frac{1}{2} (t − 1)^{2}0 = t^{2} − 6t + 3,\; t = \frac{6 \pm \sqrt{62 − 4 \cdotp 3}}{2} = 3 \pm \frac{\sqrt{24}}{2} t = 5.45 s and h = 145.5 m. Other root is less than 1 s. Check for t = 4.45 s, h = \frac{1}{2}gt2 = 97.0 m = \frac{2}{3}(145.5)
Challenge Problems
113. a. v(t) = 10t − 12t2 m/s, a(t) = 10 − 24t m/s2
b. v(2 s) = −28 m/s, a(2 s) = −38m/s2
c. The slope of the position function is zero or the velocity is zero. There are two possible solutions: t = 0, which gives x = 0, or t = \frac{10.0}{12.0} = 0.83 s, which gives x = 1.16 m. The second answer is the correct choice
d. 0.83 s
e. 1.16 m
115. 96 km/h = 26.67 m/s, a = \frac{26.67\; m/s}{4.0\; s} = 6.67m/s2, 295.38 km/h = 82.05 m/s, t = 12.3 s time to accelerate to maximum speed; x = 504.55 m = distance covered during acceleration; 7495.44 m at a constant speed; \frac{7495.44\; m}{82.05\; m/s} = 91.35 s so total time is 91.35 s + 12.3 s = 103.65 s.


