10: Rotational Motion and Angular Momentum (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
10.1: Angular Acceleration
1. Analogies exist between rotational and translational physical quantities. Identify the rotational term analogous to each of the following: acceleration, force, mass, work, translational kinetic energy, linear momentum, impulse.
2. Explain why centripetal acceleration changes the direction of velocity in circular motion but not its magnitude.
3. In circular motion, a tangential acceleration can change the magnitude of the velocity but not its direction. Explain your answer.
4. Suppose a piece of food is on the edge of a rotating microwave oven plate. Does it experience nonzero tangential acceleration, centripetal acceleration, or both when: (a) The plate starts to spin? (b) The plate rotates at constant angular velocity? (c) The plate slows to a halt?
10.3: Dynamics of Rotational Motion: Rotational Inertia
5. The moment of inertia of a long rod spun around an axis through one end perpendicular to its length is ML2/3. Why is this moment of inertia greater than it would be if you spun a point mass M at the location of the center of mass of the rod (at L/2)? (That would be ML2/4.)
6. Why is the moment of inertia of a hoop that has a mass M and a radius R greater than the moment of inertia of a disk that has the same mass and radius? Why is the moment of inertia of a spherical shell that has a mass M and a radius R greater than that of a solid sphere that has the same mass and radius?
7. Give an example in which a small force exerts a large torque. Give another example in which a large force exerts a small torque.
8. While reducing the mass of a racing bike, the greatest benefit is realized from reducing the mass of the tires and wheel rims. Why does this allow a racer to achieve greater accelerations than would an identical reduction in the mass of the bicycle’s frame?

The image shows a side view of a racing bicycle. Can you see evidence in the design of the wheels on this racing bicycle that their moment of inertia has been purposely reduced? (credit: Jesús Rodriguez)
9. A ball slides up a frictionless ramp. It is then rolled without slipping and with the same initial velocity up another frictionless ramp (with the same slope angle). In which case does it reach a greater height, and why?
10.4: Rotational Kinetic Energy: Work and Energy Revisited
10. Describe the energy transformations involved when a yo-yo is thrown downward and then climbs back up its string to be caught in the user’s hand.
11. What energy transformations are involved when a dragster engine is revved, its clutch let out rapidly, its tires spun, and it starts to accelerate forward? Describe the source and transformation of energy at each step.
12. The Earth has more rotational kinetic energy now than did the cloud of gas and dust from which it formed. Where did this energy come from?

An immense cloud of rotating gas and dust contracted under the influence of gravity to form the Earth and in the process rotational kinetic energy increased. (credit: NASA)
10.5: Angular Momentum and Its Conservation
13. When you start the engine of your car with the transmission in neutral, you notice that the car rocks in the opposite sense of the engine’s rotation. Explain in terms of conservation of angular momentum. Is the angular momentum of the car conserved for long (for more than a few seconds)?
14. Suppose a child walks from the outer edge of a rotating merry-go round to the inside. Does the angular velocity of the merry-go-round increase, decrease, or remain the same? Explain your answer.
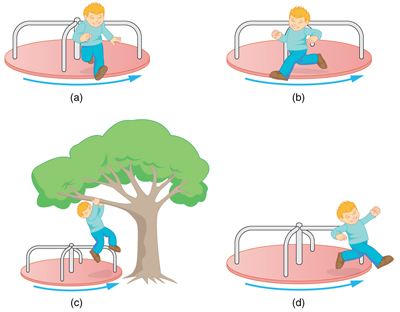
A child may jump off a merry-go-round in a variety of directions.
15. Suppose a child gets off a rotating merry-go-round. Does the angular velocity of the merry-go-round increase, decrease, or remain the same if:
(a) He jumps off radially?
(b) He jumps backward to land motionless?
(c) He jumps straight up and hangs onto an overhead tree branch?
(d) He jumps off forward, tangential to the edge? Explain your answers. (Refer to Figure).
16. Helicopters have a small propeller on their tail to keep them from rotating in the opposite direction of their main lifting blades. Explain in terms of Newton’s third law why the helicopter body rotates in the opposite direction to the blades.
17. Whenever a helicopter has two sets of lifting blades, they rotate in opposite directions (and there will be no tail propeller). Explain why it is best to have the blades rotate in opposite directions.
18. Describe how work is done by a skater pulling in her arms during a spin. In particular, identify the force she exerts on each arm to pull it in and the distance each moves, noting that a component of the force is in the direction moved. Why is angular momentum not increased by this action?
19. When there is a global heating trend on Earth, the atmosphere expands and the length of the day increases very slightly. Explain why the length of a day increases.
20. Nearly all conventional piston engines have flywheels on them to smooth out engine vibrations caused by the thrust of individual piston firings. Why does the flywheel have this effect?
21. Jet turbines spin rapidly. They are designed to fly apart if something makes them seize suddenly, rather than transfer angular momentum to the plane’s wing, possibly tearing it off. Explain how flying apart conserves angular momentum without transferring it to the wing.
22. An astronaut tightens a bolt on a satellite in orbit. He rotates in a direction opposite to that of the bolt, and the satellite rotates in the same direction as the bolt. Explain why. If a handhold is available on the satellite, can this counter-rotation be prevented? Explain your answer.
23. Competitive divers pull their limbs in and curl up their bodies when they do flips. Just before entering the water, they fully extend their limbs to enter straight down. Explain the effect of both actions on their angular velocities. Also explain the effect on their angular momenta.
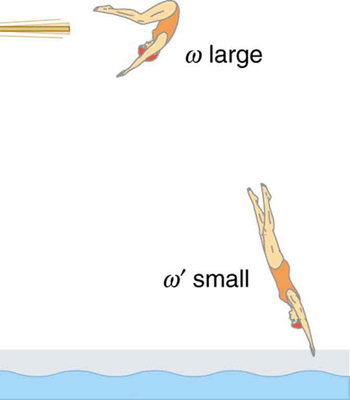
The diver spins rapidly when curled up and slows when she extends her limbs before entering the water.
24. Draw a free body diagram to show how a diver gains angular momentum when leaving the diving board.
25. In terms of angular momentum, what is the advantage of giving a football or a rifle bullet a spin when throwing or releasing it?

The image shows a view down the barrel of a cannon, emphasizing its rifling. Rifling in the barrel of a canon causes the projectile to spin just as is the case for rifles (hence the name for the grooves in the barrel). (credit: Elsie esq., Flickr)
10.6: Collisions of Extended Bodies in Two Dimensions
26. Describe two different collisions—one in which angular momentum is conserved, and the other in which it is not. Which condition determines whether or not angular momentum is conserved in a collision?
27. Suppose an ice hockey puck strikes a hockey stick that lies flat on the ice and is free to move in any direction. Which quantities are likely to be conserved: angular momentum, linear momentum, or kinetic energy (assuming the puck and stick are very resilient)?
28. While driving his motorcycle at highway speed, a physics student notices that pulling back lightly on the right handlebar tips the cycle to the left and produces a left turn. Explain why this happens.
10.7: Gyroscopic Effects: Vector Aspects of Angular Momentum
29. While driving his motorcycle at highway speed, a physics student notices that pulling back lightly on the right handlebar tips the cycle to the left and produces a left turn. Explain why this happens.
30. Gyroscopes used in guidance systems to indicate directions in space must have an angular momentum that does not change in direction. Yet they are often subjected to large forces and accelerations. How can the direction of their angular momentum be constant when they are accelerated?
Problem & Exercises
10.1: Angular Acceleration
31. At its peak, a tornado is 60.0 m in diameter and carries 500 km/h winds. What is its angular velocity in revolutions per second?
Solution
ω=0.737 rev/s
32. Integrated Concepts
An ultracentrifuge accelerates from rest to 100,000 rpm in 2.00 min.
(a) What is its angular acceleration in rad/s^2?
(b) What is the tangential acceleration of a point 9.50 cm from the axis of rotation?
(c) What is the radial acceleration in m/s^2 and multiples of g of this point at full rpm?
33. Integrated Concepts
You have a grindstone (a disk) that is 90.0 kg, has a 0.340-m radius, and is turning at 90.0 rpm, and you press a steel axe against it with a radial force of 20.0 N.
(a) Assuming the kinetic coefficient of friction between steel and stone is 0.20, calculate the angular acceleration of the grindstone.
(b) How many turns will the stone make before coming to rest?
Solution
(a) −0.26 rad/s^2
(b) 27rev
34. Unreasonable Results
You are told that a basketball player spins the ball with an angular acceleration of 100 rad/s^2.
(a) What is the ball’s final angular velocity if the ball starts from rest and the acceleration lasts 2.00 s?
(b) What is unreasonable about the result?
(c) Which premises are unreasonable or inconsistent?
10.2: Kinematics of Rotational Motion
35. With the aid of a string, a gyroscope is accelerated from rest to 32 rad/s in 0.40 s.
(a) What is its angular acceleration in rad/s2?
(b) How many revolutions does it go through in the process?
Solution
(a) 80rad/s^2
(b) 1.0 rev
36. Suppose a piece of dust finds itself on a CD. If the spin rate of the CD is 500 rpm, and the piece of dust is 4.3 cm from the center, what is the total distance traveled by the dust in 3 minutes? (Ignore accelerations due to getting the CD rotating.)
37. A gyroscope slows from an initial rate of 32.0 rad/s at a rate of 0.700 rad/s^2.
(a) How long does it take to come to rest?
(b) How many revolutions does it make before stopping?
Solution
(a) 45.7 s
(b) 116 rev
38. During a very quick stop, a car decelerates at 7.00 m/s^2.
(a) What is the angular acceleration of its 0.280-m-radius tires, assuming they do not slip on the pavement?
(b) How many revolutions do the tires make before coming to rest, given their initial angular velocity is 95.0 rad/s?
(c) How long does the car take to stop completely?
(d) What distance does the car travel in this time?
(e) What was the car’s initial velocity?
(f) Do the values obtained seem reasonable, considering that this stop happens very quickly?

Yo-yos are amusing toys that display significant physics and are engineered to enhance performance based on physical laws. (credit: Beyond Neon, Flickr)
39. Everyday application: Suppose a yo-yo has a center shaft that has a 0.250 cm radius and that its string is being pulled.
(a) If the string is stationary and the yo-yo accelerates away from it at a rate of 1.50 m/s^2, what is the angular acceleration of the yo-yo?
(b) What is the angular velocity after 0.750 s if it starts from rest?
(c) The outside radius of the yo-yo is 3.50 cm. What is the tangential acceleration of a point on its edge?
Solution
a) 600 rad/s^2
b) 450 rad/s
c) 21.0 m/s
10.3: Dynamics of Rotational Motion: Rotational Inertia
40. This problem considers additional aspects of example Calculating the Effect of Mass Distribution on a Merry-Go-Round.
(a) How long does it take the father to give the merry-go-round an angular velocity of 1.50 rad/s?
(b) How many revolutions must he go through to generate this velocity?
(c) If he exerts a slowing force of 300 N at a radius of 1.35 m, how long would it take him to stop them?
Solution
(a) 0.338 s
(b) 0.0403 rev
(c) 0.313 s
41. Calculate the moment of inertia of a skater given the following information.
(a) The 60.0-kg skater is approximated as a cylinder that has a 0.110-m radius.
(b) The skater with arms extended is approximately a cylinder that is 52.5 kg, has a 0.110-m radius, and has two 0.900-m-long arms which are 3.75 kg each and extend straight out from the cylinder like rods rotated about their ends.
42. The triceps muscle in the back of the upper arm extends the forearm. This muscle in a professional boxer exerts a force of 2.00×10^3N with an effective perpendicular lever arm of 3.00 cm, producing an angular acceleration of the forearm of 120rad/s^2. What is the moment of inertia of the boxer’s forearm?
Solution
0.50 kg⋅m^2
43. A soccer player extends her lower leg in a kicking motion by exerting a force with the muscle above the knee in the front of her leg. She produces an angular acceleration of 30.00 rad/s^2 and her lower leg has a moment of inertia of 0.750 kg⋅m^2. What is the force exerted by the muscle if its effective perpendicular lever arm is 1.90 cm?
44. Suppose you exert a force of 180 N tangential to a 0.280-m-radius 75.0-kg grindstone (a solid disk).
(a)What torque is exerted?
(b) What is the angular acceleration assuming negligible opposing friction?
(c) What is the angular acceleration if there is an opposing frictional force of 20.0 N exerted 1.50 cm from the axis?
Solution
(a) 50.4 N⋅m
(b) 17.1rad/s^2
(c) 17.0rad/s^2
45. Consider the 12.0 kg motorcycle wheel shown in Figure. Assume it to be approximately an annular ring with an inner radius of 0.280 m and an outer radius of 0.330 m. The motorcycle is on its center stand, so that the wheel can spin freely.
(a) If the drive chain exerts a force of 2200 N at a radius of 5.00 cm, what is the angular acceleration of the wheel?
(b) What is the tangential acceleration of a point on the outer edge of the tire?
(c) How long, starting from rest, does it take to reach an angular velocity of 80.0 rad/s?
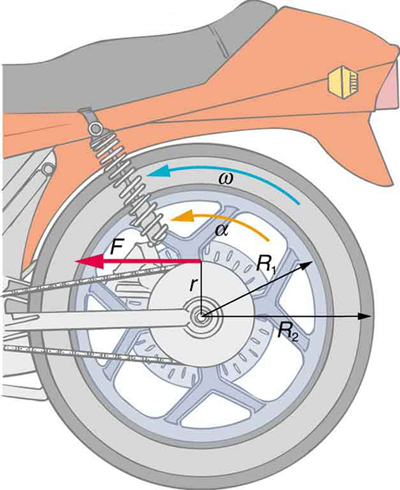
A motorcycle wheel has a moment of inertia approximately that of an annular ring.
46. Zorch, an archenemy of Superman, decides to slow Earth’s rotation to once per 28.0 h by exerting an opposing force at and parallel to the equator. Superman is not immediately concerned, because he knows Zorch can only exert a force of 4.00×10^7N (a little greater than a Saturn V rocket’s thrust). How long must Zorch push with this force to accomplish his goal? (This period gives Superman time to devote to other villains.) Explicitly show how you follow the steps found in Problem-Solving Strategy for Rotational Dynamics.
Solution
3.96×10^{18}s or 1.26×10^{11}y
47. An automobile engine can produce 200 N ∙ m of torque. Calculate the angular acceleration produced if 95.0% of this torque is applied to the drive shaft, axle, and rear wheels of a car, given the following information. The car is suspended so that the wheels can turn freely. Each wheel acts like a 15.0 kg disk that has a 0.180 m radius. The walls of each tire act like a 2.00-kg annular ring that has inside radius of 0.180 m and outside radius of 0.320 m. The tread of each tire acts like a 10.0-kg hoop of radius 0.330 m. The 14.0-kg axle acts like a rod that has a 2.00-cm radius. The 30.0-kg drive shaft acts like a rod that has a 3.20-cm radius.
48. Starting with the formula for the moment of inertia of a rod rotated around an axis through one end perpendicular to its length (I=Mℓ^2/3) , prove that the moment of inertia of a rod rotated about an axis through its center perpendicular to its length is I=Mℓ^2/12. You will find the graphics in Figure useful in visualizing these rotations.
Solution
I_{end}=I_{center}+m(\frac{l}{2})^2
Thus,I_{center}=I_{end}−\frac{1}{4}ml^2=\frac{1}{3}ml^2−\frac{1}{4}ml^2=\frac{1}{12}ml^2
49. Unreasonable Results
A gymnast doing a forward flip lands on the mat and exerts a 500-N ∙ m torque to slow and then reverse her angular velocity. Her initial angular velocity is 10.0 rad/s, and her moment of inertia is 0.050kg⋅m^2.
(a) What time is required for her to exactly reverse her spin?
(b) What is unreasonable about the result?
(c) Which premises are unreasonable or inconsistent?
Solution
(a) 2.0 ms
(b) The time interval is too short.
(c) The moment of inertia is much too small, by one to two orders of magnitude. A torque of 500 N⋅m is reasonable.
50. Unreasonable Results
An advertisement claims that an 800-kg car is aided by its 20.0-kg flywheel, which can accelerate the car from rest to a speed of 30.0 m/s. The flywheel is a disk with a 0.150-m radius.
(a) Calculate the angular velocity the flywheel must have if 95.0% of its rotational energy is used to get the car up to speed.
(b) What is unreasonable about the result?
(c) Which premise is unreasonable or which premises are inconsistent?
Solution
(a) 17,500 rpm
(b) This angular velocity is very high for a disk of this size and mass. The radial acceleration at the edge of the disk is > 50,000 gs.
(c) Flywheel mass and radius should both be much greater, allowing for a lower spin rate (angular velocity).
10.4: Rotational Kinetic Energy: Work and Energy Revisited
51. This problem considers energy and work aspects of [link]—use data from that example as needed.
(a) Calculate the rotational kinetic energy in the merry-go-round plus child when they have an angular velocity of 20.0 rpm.
(b) Using energy considerations, find the number of revolutions the father will have to push to achieve this angular velocity starting from rest.
(c) Again, using energy considerations, calculate the force the father must exert to stop the merry-go-round in two revolutions
Solution
(a) 185 J
(b) 0.0785 rev
(c) W=9.81 N
52. What is the final velocity of a hoop that rolls without slipping down a 5.00-m-high hill, starting from rest?
53. (a) Calculate the rotational kinetic energy of Earth on its axis. (b) What is the rotational kinetic energy of Earth in its orbit around the Sun?
Solution
(a) 2.57×10^{29}J
(b) KE_{rot}=2.65×10^{33}J
54. Calculate the rotational kinetic energy in the motorcycle wheel ([link]) if its angular velocity is 120 rad/s. Assume M = 12.0 kg, R_1 = 0.280 m, and R_2 = 0.330 m.
55. A baseball pitcher throws the ball in a motion where there is rotation of the forearm about the elbow joint as well as other movements. If the linear velocity of the ball relative to the elbow joint is 20.0 m/s at a distance of 0.480 m from the joint and the moment of inertia of the forearm is 0.500 kg⋅m^2, what is the rotational kinetic energy of the forearm?
Solution
KE_{rot}=434 J
56. While punting a football, a kicker rotates his leg about the hip joint. The moment of inertia of the leg is 3.75 kg⋅m^2 and its rotational kinetic energy is 175 J.
(a) What is the angular velocity of the leg?
(b) What is the velocity of tip of the punter’s shoe if it is 1.05 m from the hip joint?
(c) Explain how the football can be given a velocity greater than the tip of the shoe (necessary for a decent kick distance).
57. A bus contains a 1500 kg flywheel (a disk that has a 0.600 m radius) and has a total mass of 10,000 kg.
(a) Calculate the angular velocity the flywheel must have to contain enough energy to take the bus from rest to a speed of 20.0 m/s, assuming 90.0% of the rotational kinetic energy can be transformed into translational energy.
(b) How high a hill can the bus climb with this stored energy and still have a speed of 3.00 m/s at the top of the hill? Explicitly show how you follow the steps in the Problem-Solving Strategy for Rotational Energy.
Solution
(a) 128 rad/s
(b) 19.9 m
58. A ball with an initial velocity of 8.00 m/s rolls up a hill without slipping. Treating the ball as a spherical shell, calculate the vertical height it reaches.
(b) Repeat the calculation for the same ball if it slides up the hill without rolling.
59. While exercising in a fitness center, a man lies face down on a bench and lifts a weight with one lower leg by contacting the muscles in the back of the upper leg.
(a) Find the angular acceleration produced given the mass lifted is 10.0 kg at a distance of 28.0 cm from the knee joint, the moment of inertia of the lower leg is 0.900 kg⋅m^2, the muscle force is 1500 N, and its effective perpendicular lever arm is 3.00 cm.
(b) How much work is done if the leg rotates through an angle of 20.0º with a constant force exerted by the muscle?
Solution
(a) 10.4 rad/s^2
(b) net W=6.11 J
60. To develop muscle tone, a woman lifts a 2.00-kg weight held in her hand. She uses her biceps muscle to flex the lower arm through an angle of 60.0º.
(a) What is the angular acceleration if the weight is 24.0 cm from the elbow joint, her forearm has a moment of inertia of 0.250 kg⋅m^2, and the net force she exerts is 750 N at an effective perpendicular lever arm of 2.00 cm?
(b) How much work does she do?
61. Consider two cylinders that start down identical inclines from rest except that one is frictionless. Thus one cylinder rolls without slipping, while the other slides frictionlessly without rolling. They both travel a short distance at the bottom and then start up another incline.
(a) Show that they both reach the same height on the other incline, and that this height is equal to their original height.
(b) Find the ratio of the time the rolling cylinder takes to reach the height on the second incline to the time the sliding cylinder takes to reach the height on the second incline.
(c) Explain why the time for the rolling motion is greater than that for the sliding motion.
62. What is the moment of inertia of an object that rolls without slipping down a 2.00-m-high incline starting from rest, and has a final velocity of 6.00 m/s? Express the moment of inertia as a multiple of MR^2, where M is the mass of the object and R is its radius.
63. Suppose a 200-kg motorcycle has two wheels like, the one described in Problem 10.15 and is heading toward a hill at a speed of 30.0 m/s.
(a) How high can it coast up the hill, if you neglect friction?
(b) How much energy is lost to friction if the motorcycle only gains an altitude of 35.0 m before coming to rest?
64. In softball, the pitcher throws with the arm fully extended (straight at the elbow). In a fast pitch the ball leaves the hand with a speed of 139 km/h.
(a) Find the rotational kinetic energy of the pitcher’s arm given its moment of inertia is 0.720 kg⋅m^2 and the ball leaves the hand at a distance of 0.600 m from the pivot at the shoulder.
(b) What force did the muscles exert to cause the arm to rotate if their effective perpendicular lever arm is 4.00 cm and the ball is 0.156 kg?
Solution
(a) 1.49 kJ
(b) 2.52×10^4N
65. Construct Your Own Problem
Consider the work done by a spinning skater pulling her arms in to increase her rate of spin. Construct a problem in which you calculate the work done with a “force multiplied by distance” calculation and compare it to the skater’s increase in kinetic energy.
10.5: Angular Momentum and Its Conservation
66. (a) Calculate the angular momentum of the Earth in its orbit around the Sun.
(b) Compare this angular momentum with the angular momentum of Earth on its axis.
Solution
(a) 2.66×10^{40}kg⋅m^2/s
(b) 7.07×10^{33}kg⋅m^2/s
The angular momentum of the Earth in its orbit around the Sun is 3.77×10^6 times larger than the angular momentum of the Earth around its axis.
67. (a) What is the angular momentum of the Moon in its orbit around Earth?
(b) How does this angular momentum compare with the angular momentum of the Moon on its axis? Remember that the Moon keeps one side toward Earth at all times.
(c) Discuss whether the values found in parts (a) and (b) seem consistent with the fact that tidal effects with Earth have caused the Moon to rotate with one side always facing Earth.
68. Suppose you start an antique car by exerting a force of 300 N on its crank for 0.250 s. What angular momentum is given to the engine if the handle of the crank is 0.300 m from the pivot and the force is exerted to create maximum torque the entire time?
Solution
22.5 kg⋅m^2/s
69. A playground merry-go-round has a mass of 120 kg and a radius of 1.80 m and it is rotating with an angular velocity of 0.500 rev/s. What is its angular velocity after a 22.0-kg child gets onto it by grabbing its outer edge? The child is initially at rest.
70. Three children are riding on the edge of a merry-go-round that is 100 kg, has a 1.60-m radius, and is spinning at 20.0 rpm. The children have masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg moves to the center of the merry-go-round, what is the new angular velocity in rpm?
Solution
25.3 rpm
71. (a) Calculate the angular momentum of an ice skater spinning at 6.00 rev/s given his moment of inertia is 0.400kg⋅m^2.
(b) He reduces his rate of spin (his angular velocity) by extending his arms and increasing his moment of inertia. Find the value of his moment of inertia if his angular velocity decreases to 1.25 rev/s.
(c) Suppose instead he keeps his arms in and allows friction of the ice to slow him to 3.00 rev/s. What average torque was exerted if this takes 15.0 s?
72. Construct Your Own Problem
Consider the Earth-Moon system. Construct a problem in which you calculate the total angular momentum of the system including the spins of the Earth and the Moon on their axes and the orbital angular momentum of the Earth-Moon system in its nearly monthly rotation. Calculate what happens to the Moon’s orbital radius if the Earth’s rotation decreases due to tidal drag. Among the things to be considered are the amount by which the Earth’s rotation slows and the fact that the Moon will continue to have one side always facing the Earth.
10.6: Collisions of Extended Bodies in Two Dimensions
73. Repeat Example in which the disk strikes and adheres to the stick 0.100 m from the nail.
Solution
(a) 0.156 rad/s
(b) 1.17×10^{−2}J
(c) 0.188 kg⋅m/s
74. Repeat Example in which the disk originally spins clockwise at 1000 rpm and has a radius of 1.50 cm.
75. Twin skaters approach one another as shown in Figure and lock hands.
(a) Calculate their final angular velocity, given each had an initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg, and each has a center of mass located 0.800 m from their locked hands. You may approximate their moments of inertia to be that of point masses at this radius.
(b) Compare the initial kinetic energy and final kinetic energy.
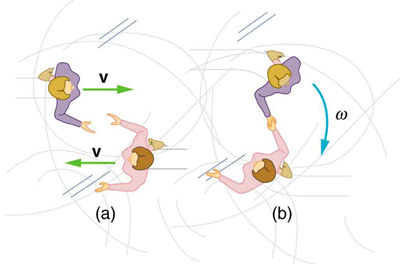
Twin skaters approach each other with identical speeds. Then, the skaters lock hands and spin.
Solution
(a) 3.13 rad/s
(b) Initial KE = 438 J, final KE = 438 J
76. Suppose a 0.250-kg ball is thrown at 15.0 m/s to a motionless person standing on ice who catches it with an outstretched arm as shown in Figure.
(a) Calculate the final linear velocity of the person, given his mass is 70.0 kg.
(b) What is his angular velocity if each arm is 5.00 kg? You may treat the ball as a point mass and treat the person's arms as uniform rods (each has a length of 0.900 m) and the rest of his body as a uniform cylinder of radius 0.180 m. Neglect the effect of the ball on his center of mass so that his center of mass remains in his geometrical center.
(c) Compare the initial and final total kinetic energies.
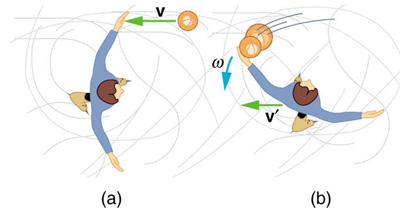
The figure shows the overhead view of a person standing motionless on ice about to catch a ball. Both arms are outstretched. After catching the ball, the skater recoils and rotates.
77. Repeat Example in which the stick is free to have translational motion as well as rotational motion.
Solution
(a) 1.70 rad/s
(b) Initial KE = 22.5 J, final KE = 2.04 J
(c) 1.50 kg⋅m/s
10.7: Gyroscopic Effects: Vector Aspects of Angular Momentum
78. Integrated Concepts
The axis of Earth makes a 23.5° angle with a direction perpendicular to the plane of Earth’s orbit. As shown in Figure, this axis precesses, making one complete rotation in 25,780 y.
(a) Calculate the change in angular momentum in half this time.
(b) What is the average torque producing this change in angular momentum?
(c) If this torque were created by a single force (it is not) acting at the most effective point on the equator, what would its magnitude be?
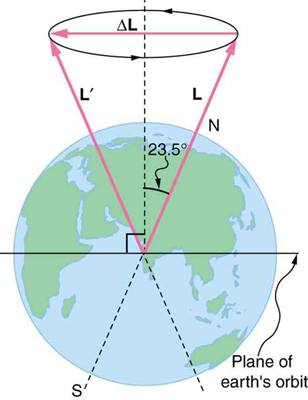
The Earth’s axis slowly precesses, always making an angle of 23.5° with the direction perpendicular to the plane of Earth’s orbit. The change in angular momentum for the two shown positions is quite large, although the magnitude L size 12{L} {} is unchanged.
Solution
(a) 5.64×10^{33}kg⋅m^2/s
(b) 1.39×10^{22}N⋅m
(c) 2.17×10^{15}N
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

