Skip to main content
Physics LibreTexts

11.4: Other Applications

  1. Last updated
  2. Save as PDF
  • Page ID
    14504
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    learning objectives

    • Predict if flow will be laminar or turbulent

    It is possible to predict if flow will be laminar or turbulent. At low velocity, flow in a very smooth tube or around a smooth, streamlined object will be laminar. At high velocity, even the flow in a smooth tube or around a smooth object will experience turbulence. However, between low and high velocity, flow is more difficult to predict. In fact, at intermediate velocities, flow may oscillate back and forth indefinitely between laminar and turbulent.

    An occlusion (narrowing) of an artery, such as shown in, is likely to cause turbulence because of the irregularity of the blockage, as well as the complexity of blood as a fluid. Turbulence in the circulatory system (such as aneurysms, or ballooning of arteries) is noisy and can sometimes be detected with a stethoscope (such as when measuring diastolic pressure in the upper arm’s partially collapsed brachial artery). These turbulent sounds, at the onset of blood flow when the cuff pressure becomes sufficiently small, are called Korotkoff sounds. Heart murmurs, consistent with their name, are sounds produced by turbulent flow around damaged and insufficiently closed heart valves. Another method of detecting this type of turbulence is ultrasound, used as a medical indicator in a process analogous to Doppler-shift radar (used to detect storms).

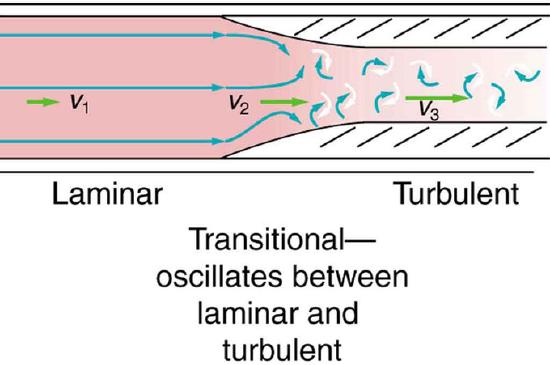
    image

    Turbulent Flow in an Artery: Flow is laminar in the large part of this blood vessel and turbulent in the part narrowed by plaque, where velocity is high. In the transition region, the flow can oscillate chaotically between laminar and turbulent flow.

    Turbulence manifests in other areas, with varying causes. During an airplane flight, for example, the turbulence experienced is due to the mixing of warm and cold air in the atmosphere, causing the airplane to shake. The mixing currents in oceans creates a similar effect.

    The phenomenon of turbulent air flow must be accounted for in many applications. For example, race cars are unable to follow each other around fast corners because the leading car creates turbulent air flow in its wake (this can lead to under-steering).

    Industrial equipment, such as pipes, ducts, and heat exchangers are often designed to induce the flow regime of interest (laminar or turbulent). When flow is turbulent, particles exhibit additional transverse motion. This enhances the rate of energy and momentum exchange between them, increasing the heat transfer. Turbulent flow is thus desirable in applications where a relatively cool fluid is mixed with a warmer fluid to reduce the temperature of the warmer fluid.

    It is imperative to take into account turbulent flow when designing certain structures, such as a bridge support, as shown in. In the late summer and fall, when river flow is slow, water flows smoothly around the support legs. In the spring, when the flow is faster, the flow may start off laminar but it is quickly separated from the leg and becomes turbulent. The bridge supports must be designed so that they can withstand the turbulent flow of the water in the spring.

    image

    Longtown Bridge: Turbulent flow is visible around the bridge supports of the Longtown bridge.

    Motionof an Object in a Viscous Field

    Objects moving in a viscous fluid feel a resistive force proportional to the viscosity of the fluid.

    learning objectives

    • Assess the relationship of the parameters to one another in determining the inertia of an object moving in fluid

    Overview

    A moving object in a viscous fluid is equivalent to a stationary object in a flowing fluid stream. (For example, when you ride a bicycle at 10 m/s in still air, you feel the air in your face exactly as if you were stationary in a 10-m/s wind. ) Flow of the stationary fluid around a moving object may be laminar, turbulent, or a combination of the two. Just as with flow in tubes, it is possible to predict when a moving object creates turbulence. We use another form of the Reynolds number N′R, defined for an object moving in a fluid to be

    \[\mathrm{N‘R=\dfrac{ρvL}{η}}\]

    where L is a characteristic length of the object (a sphere’s diameter, for example), the fluid density, its viscosity, and v the object’s speed in the fluid. If N′R is less than about 1, flow around the object can be laminar, particularly if the object has a smooth shape. The transition to turbulent flow occurs for N′R between 1 and about 10, depending on surface roughness and so on. Depending on the surface, there can be a turbulent wake behind the object with some laminar flow over its surface. For an N′R between 10 and 10^6, the flow may be either laminar or turbulent and may oscillate between the two. For N′R greater than about 10^6, the flow is entirely turbulent, even at the surface of the object. (See. ) Laminar flow occurs mostly when the objects in the fluid are small, such as raindrops, pollen, and blood cells in plasma.

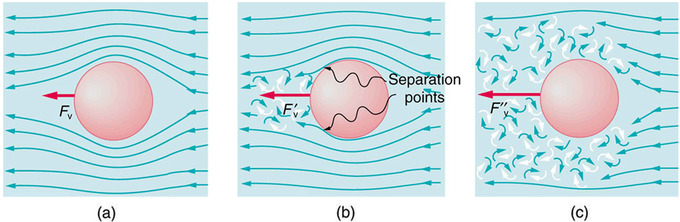
    image

    Motion of an object in a viscous fluid.: (a) Motion of this sphere to the right is equivalent to fluid flow to the left. Here the flow is laminar with N′R less than 1. There is a force, called viscous drag FV, to the left on the ball due to the fluid’s viscosity. (b) At a higher speed, the flow becomes partially turbulent, creating a wake starting where the flow lines separate from the surface. Pressure in the wake is less than in front of the sphere, because fluid speed is less, creating a net force to the left F′V that is significantly greater than for laminar flow. Here N′R is greater than 10. (c) At much higher speeds, where N′R is greater than 10^6, flow becomes turbulent everywhere on the surface and behind the sphere. Drag increases dramatically.

    Viscous Drag

    One of the consequences of viscosity is a resistance force called viscous drag FVFV that is exerted on a moving object. This force typically depends on the object’s speed (in contrast with simple friction). Experiments have shown that for laminar flow (N′R less than about one) viscous drag is proportional to speed, whereas for N′R between about 10 and 106, viscous drag is proportional to speed squared. (This relationship is a strong dependence and is pertinent to bicycle racing, where even a small headwind causes significantly increased drag on the racer. Cyclists take turns being the leader in the pack for this reason. ) For N′R greater than 106, drag increases dramatically and behaves with greater complexity. For laminar flow around a sphere, FVFV is proportional to fluid viscosity, the object’s characteristic size L, and its speed v. All of which makes sense—the more viscous the fluid and the larger the object, the more drag we expect. Recall Stoke’s law FS=6πrηvFS=6πrηv. For the special case of a small sphere of radius R, moving slowly in a fluid of viscosity, the drag force FSFS is given by

    FS=6πRηvFS=6πRηv.

    Molecular Transport Phenomena

    Molecular transport phenomena are ways in which molecules are transported from one region to another. These include diffusion and osmosis.

    learning objectives

    • Predict the role diffusion plays in blood transport throughout the body

    Diffusion

    Atoms and molecules are in constant motion at any temperature. In fluids they move about randomly even in the absence of macroscopic flow.

    Diffusion is the movement of substances due to random thermal molecular motion. Fluids, like fish fumes or odors entering ice cubes, can even diffuse through solids. Diffusion is a slow process over macroscopic distances. The densities of common materials are great enough that molecules cannot travel very far before having a collision that can scatter them in any direction, including straight backward. More massive molecules diffuse more slowly.

    Another interesting point is that the diffusion rate for oxygen in air is much greater than for oxygen in water. In water, an oxygen molecule makes many more collisions in its random walk and is slowed considerably. In water, an oxygen molecule moves only about 40μm in 1 s. (Each molecule actually collides about 1010 times per second!). Finally, note that diffusion constants increase with temperature, because average molecular speed increases with temperature. This is because the average kinetic energy of molecules, 1/2mv2, is proportional to absolute temperature. Because diffusion is typically very slow, its most important effects occur over small distances. For example, the cornea of the eye gets most of its oxygen by diffusion through the thin tear layer covering it.

    If you very carefully place a drop of food coloring in a still glass of water, it will slowly diffuse into the colorless surroundings until its concentration is the same everywhere. This type of diffusion is called free diffusion, because there are no barriers inhibiting it. Let us examine its direction and rate. Molecular motion is random in direction, and so simple chance dictates that more molecules will move out of a region of high concentration than into it. The net rate of diffusion is higher initially than after the process is partially completed. The rate of diffusion is proportional to the concentration difference. Many more molecules will leave a region of high concentration than will enter it from a region of low concentration. In fact, if the concentrations were the same, there would be no net movement. The rate of diffusion is also proportional to the diffusion constant D, which is determined experimentally. Many of the factors that affect the rate are hidden in the diffusion constant D. For example, temperature and cohesive and adhesive forces all affect values of D. Diffusion is the dominant mechanism by which the exchange of nutrients and waste products occur between the blood and tissue, and between air and blood in the lungs. In the evolutionary process, as organisms became larger, they needed quicker methods of transportation than net diffusion, because of the larger distances involved in the transport, leading to the development of circulatory systems. Less sophisticated, single-celled organisms still rely totally on diffusion for the removal of waste products and the uptake of nutrients.

    image

    Food Coloring: Food coloring spreading on a thin water film.

    Osmosis and Dialysis – Diffusion Across Different Membranes

    Some of the most interesting examples of diffusion occur through barriers that affect the rates of diffusion. For example, when you soak a swollen ankle in Epsom salt, water diffuses through your skin. Many substances regularly move through cell membranes; oxygen moves in, carbon dioxide moves out, nutrients go in, and wastes go out, for example. Because membranes are thin structures (typically 6.5×10−9 to 10×10−9 m across) diffusion rates through them can be high.

    Diffusion through membranes is an important method of transport. Membranes are generally selectively permeable, or semipermeable. In other types of membranes, the molecules may actually dissolve in the membrane or react with molecules in the membrane while moving across. Membrane function, in fact, is the subject of much current research, involving not only physiology but also chemistry and physics. Osmosis is driven by the imbalance in water concentration. For example, water is more concentrated in your body than in Epsom salt. When you soak a swollen ankle in Epsom salt, the water moves out of your body into the lower-concentration region in the salt. Similarly, dialysis is the transport of any other molecule through a semipermeable membrane due to its concentration difference. Both osmosis and dialysis are used by the kidneys to cleanse the blood.

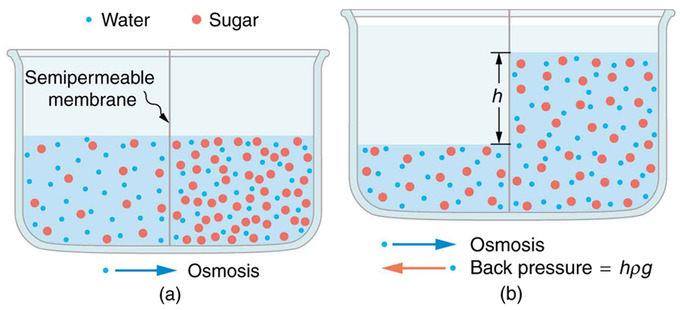
    image

    Diffusion: (a) Two sugar-water solutions of different concentrations, separated by a semipermeable membrane that passes water but not sugar. Osmosis will be to the right, since water is less concentrated there. (b) The fluid level rises until the back pressure ρgh equals the relative osmotic pressure; then, the net transfer of water is zero.

    Pumps and the Heart

    The heart pumps blood through the body by contracting and relaxing, increasing and decreasing the pressure.

    learning objectives

    • Contrast systole and diastole in cardiovascular circulation

    The Heart and its Parts

    The heart is made up of four chambers. Two atria at the top of the heart receive blood and two ventricles at the bottom of the heart pump blood out of the heart. The septum divides the left and right side of the heart, while the valves of the heart ensure that blood only flows in one direction.They include the tricuspid valve-found between the right atrium and the right ventricle-and the mitral valve-found between the left atrium and the left ventricle. The list of heart valves also includes the semi-lunar valves, which are located at the bottom of the aorta and pulmonary artery. Strong tendinous chords attached to valves prevent them from turning inside out when they close.

    The human heart will undergo over 3 billion contraction cycles during a normal lifetime. A complete cardiac cycle is one round of the heart pumping blood and consists of two parts: systole (contraction of the heart muscle) and diastole (relaxation of the heart muscle). During the cycle, the top half of the heart works as one unit, while the bottom half of the heart works as one unit.

    The heart beat can be heard as a sound that the valves make when they close. The ‘lub’ sound is made when the atrio ventricular valves close and the ‘dub’ sound is made when the semi lunar valves close. Blood pressure is produced by the left ventricle contractions.The rhythm of ventricle diastole, often just referred to as diastole, causes the pulse, which can be felt by holding two fingers to the side of the throat.

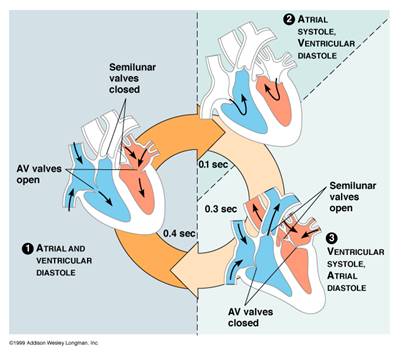
    image

    Cardiac Cycle: The heart pumps blood through the body.

    Key Points

    • For low velocity, flow in a smooth tube will be laminar.
    • At higher velocities or if there are obstructions, the flow turns turbulent.
    • Turbulent flow is very chaotic, with rapid variations in velocity and pressure.
    • Viscous fluids exert a resitive force on objects attempting to move through them.
    • This resistive force is called viscous drag and is proportional to the viscosity of the fluid and the motion of the object.
    • An object moving in a fluid can be thought of as a stationary object in a moving fluid.
    • Diffusion is the movement of molecules due to random thermal motion.
    • Osmosis is the movement of molecules due to different concentrations. Molecules will move from regions of high concentrations to lower concentrations.
    • These transport phenomena can take place through membranes if the pressure is great enough.

    Key Terms

    • turbulent: Being in, or causing, disturbance or unrest.
    • streamlined: Designed to offer little resistance to the flow of fluid, especially by having sleek, graceful lines.
    • laminar: Of fluid motion, smooth and regular, flowing as though in different layers.
    • viscosity: A quantity expressing the magnitude of internal friction in a fluid, as measured by the force per unit area resisting uniform flow.
    • turbulence: Disturbance in a gas or fluid, characterized by evidence of internal motion or unrest.
    • diffusion: the intermingling of the molecules of a fluid due to random thermal agitation
    • ventricle: One of two lower chambers of the heart.
    • contraction: A reversible reduction in size.
    • atrium: An upper chamber of the heart that receives blood from the veins and forces it into a ventricle. In higher vertebrates, the right atrium receives blood from the superior vena cava and inferior vena cava, and the left atrium receives blood from the left and right pulmonary veins.

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    This page titled 11.4: Other Applications is shared under a not declared license and was authored, remixed, and/or curated by Boundless.