Skip to main content
Physics LibreTexts

16.2: Sound Intensity and Level

  1. Last updated
  2. Save as PDF
  • Page ID
    14537
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    learning objectives

    • Calculate sound intensity from power

    Overview of Intensity

    Sound Intensity is the power per unit area carried by a wave. Power is the rate that energy is transferred by a wave.

    Sound Intensity and Decibels

    The equation used to calculate this intensity, I, is:I\(\mathrm{I=\frac{P}{A}}\)Where P is the power going through the area, A. The SI unit for intensity is watts per meter squared or,Wm2Wm2. This is the general intensity formula, but lets look at it from a sound perspective.

    Sound Intensity

    Sound intensity can be found from the following equation: \(\mathrm{I=\frac{Δp^2}{2ρv_w}}\). Δp – change in pressure, or amplitudeρ – density of the material the sound is traveling throughvw – speed of observed sound.Now we have a way to calculate the sound intensity, so lets talk about observed intensity. The pressure variation, amplitude, is proportional to the intensity, So it is safe to say that the larger your sound wave oscillation, the more intense your sound will be. This figure shows this concept.

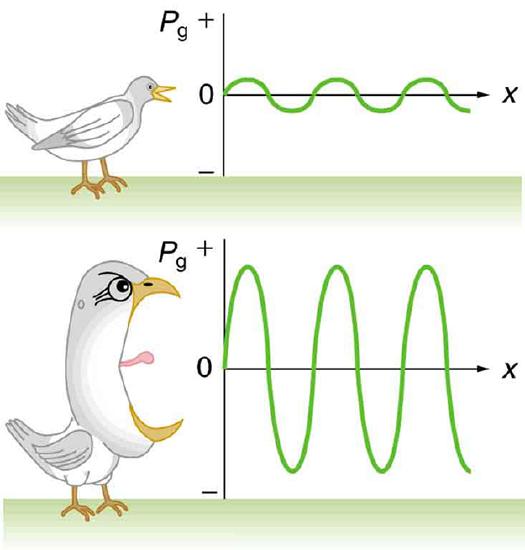
    image

    Sound Intensity: Graphs of the gauge pressures in two sound waves of different intensities. The more intense sound is produced by a source that has larger-amplitude oscillations and has greater pressure maxima and minima. Because pressures are higher in the greater-intensity sound, it can exert larger forces on the objects it encounters

    Although the units for sound intensity are technically watts per meter squared, it is much more common for it to be referred to as decibels, dB. A decibel is a ratio of the observed amplitude, or intensity level to a reference, which is 0 dB. The equation for this is: \(\mathrm{β=10 \log _{10} \frac{I}{I_0}β}\) – decibel levelI – Observed intensityI0– Reference intensity.For more on decibels, please refer to the Decibel Atom.

    For a reference point on intensity levels, below are a list of a few different intensities:

    • 0 dB, I = 1×10-12 –> Threshold of human hearing
    • 10 dB, I = 1×10-11 –> Rustle of leaves
    • 60 dB, I = 1×10-6 –> Normal conversation
    • 100 dB, I = 1×10-2 –> Loud siren
    • 160 dB, I = 1×104–> You just burst your eardrums

    Human Perception of Sound

    The study of human perception of sound is called psychoacoustics.

    Skills to Develop

    • Explain how frequency is perceived by humans

    The study of the human perception of sound is called psychoacoustics. Many factors go into hearing, including wave properties, sensory and brain processes. First, the wave has to be made, and it has a specific wavelength and frequency. Then the sound wave reaches the human ear, and is processed through many areas. Finally, the sound wave makes it through the ear and to the human brain, where even more action happens. You might think that when something makes a noise that you hear it instantaneously but, in reality, it goes through many steps first.

    Wave Properties

    We are not going to go into too much detail about the wave’s physical properties, since it is out of the scope of this atom, but remember:

    • Frequency is perceived by humans as pitch;
    • The sound intensity is the amplitude;
    • Humans can only hear a specific range of sound, usually from 20 Hz to 20,000 Hz;
    • The factors that go into a sound are its intensity, frequency and overtones (which are like interference, or background noises).

    The Human Ear

    The human ear is made up of three main sections, as shown in:

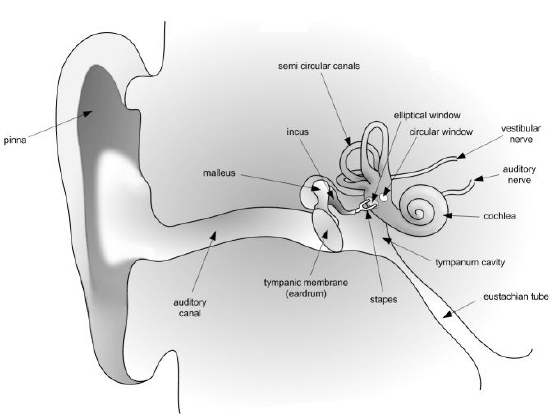
    image

    The Human Ear: A detailed diagram of the human ear.

    1. The outer ear
    2. The middle ear
    3. The inner ear

    We are going to start where a sound wave would start and follow it on its journey from outside your ear all the way to your brain. When you look at someone’s ear, you are really only seeing the pinna, the outer most portion of the ear. It collects and focuses the sound wave. The wave then goes through your ear canal to the eardrum. The sound waves cause the eardrum to vibrate. Then we are in the middle ear, which has three very, very small bones: the malleus, incus and stapes. These can also be referred to as the hammer, anvil and stirrup, respectively. These three bones transmit the signal to the elliptical window. This is the beginning of the inner ear. The sound waves are then transmitted from the elliptical window through the inner ear’s semicircular canals, the cochlea, and the audio nerve, which is filled with fluid. This fluid is what allows the body to detect movements and maintain balance. Your cochlea is shaped like a snail, and is full of teeny tiny hairs. These hairs vibrate differently depending on the frequencies. These vibrations release electrical impulses to the auditory nerve and are then sent to your brain, where they are understood as sound. So while this seems to happen very quickly, sound waves have to travel a long way before you ever hear anything!

    Decibels

    The decibel is a logarithmic unit used to quantify sound levels, by comparing a physical quantity to a reference level.

    Skills to Develop

    • Identify how decibel is quantified in acoustics

    The decibel, dB, is commonly used to quantify sound levels, although it is not a unit of sound, but a unit of pressure. The decibel is a logarithmic unit that indicates the ratio if a physical quantity to a reference level. It is one tenth of a Bel, which was named after the inventor of the telephone, Alexander Graham Bell. The word decibell comes from the prefix, deci, that is 1/10 of the word it precedes For more information on how to convert units, refer to the unit conversion atom. Although the decibel can be used to talk about a number of different subjects, in this atom we are going to cover its use in acoustics and sound level.

    In acoustics, the decibel is quantified relative to a reference which has been set at a sound pressure level of 20 micropascals, and is called a 0 dB. This reference level is a typical threshold of human hearing perception. The following equation is used to calculate the sound pressure level, or amplitude: \(\mathrm{amplitude[dB]=20 \log _{10}\frac{s}{s_o}}\)so is the reference pressure which is 20 micropascals or 0 dB, and s is the observed sound pressure.The human ear has a standard sound threshold of 120 dB, which expressed logarithmically is around 1012. This is a standard threshold, but it also depends on frequency. Loudness is a measure of sound intensity taking frequency into account, and is called a A-weighted decibel, dB(A), or a phon. This figure shows The Fletcher Munson Chart, which demonstrates the different sound frequencies and decibels that the human ear perceives as the same.

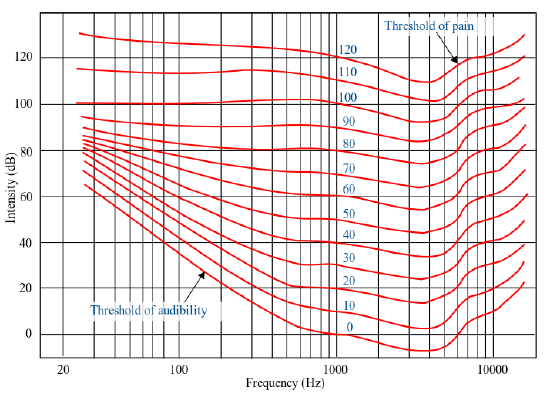
    image

    The Fletcher Munson Chart: The Fletcher-Munson equal-loudness contours. Phons are labelled in blue

    Key Points

    • Sound intensity can be found from the following equation: \(\mathrm{I=\frac{Δp^2}{2ρv_w}}\). Δ p – change in pressure, or amplitude ρ – density of the material the sound is traveling through vw– speed of observed sound.
    • The larger your sound wave oscillation, the more intense your sound will be.
    • Although the units for sound intensity are technically watts per meter squared, it is much more common for it to be referred to as decibels, dB.
    • Frequency is perceived by humans as pitch. The sound intensity is what humans can hear, and is generally only a specific range of sound, usually from 20 Hz to 20,000 Hz. The factors that go into a sound are its intensity, frequency and overtones (which are like interference or background noises).
    • Your ear is made up of three major sections: the inner, middle and outer ear.
    • Your cochlea, which is in your inner ear, not only transmits sound waves to your brain, but also contains a liquid that helps humans maintain their balance.
    • In acoustics, the decibel is quantified relative to a reference which has been set at a sound pressure level of 20 micropascals, and is called a 0 dB.
    • The following equation is used to calculate the sound pressure level, or amplitude: \(\mathrm{amplitude[dB]=20 \log_{10} \frac{s}{s_o}}\). \(\mathrm{s_o}\) is the reference pressure which is 20 micropascals or 0 dB, and s is the observed sound pressure.
    • The human ear has a standard sound threshold of 120 dB, which expressed logarithmically is around 1012. This is a standard threshold, but it also depends on frequency. Loudness is a measure of sound intensity taking frequency into account, and is called a A-weighted decibel, dB(A), or a phon.

    Key Terms

    • decibel: A common measure of sound intensity that is one tenth of a bel on the logarithmic intensity scale. It is defined as \(\mathrm{dB=10 \log_{10}(P_1/P_2)}\), where \(\mathrm{P_1}\) and \(\mathrm{P_2}\) are the relative powers of the sound.
    • amplitude: The maximum absolute value of some quantity that varies.
    • eardrum: A thin membrane that separates the outer ear from the middle ear and transmits sound from the air to the malleus.
    • cochlea: The complex, spirally coiled, tapered cavity of the inner ear in which sound vibrations are converted into nerve impulses.
    • phon: A unit of apparent loudness, equal in number to the intensity in decibels of a 1,000-hertz tone judged to be as loud as the sound being measured.

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    This page titled 16.2: Sound Intensity and Level is shared under a not declared license and was authored, remixed, and/or curated by Boundless.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      Boundless
      Show TOC
      no
    2. Tags
      1. Amplitude
      2. cochlea
      3. decibels (units)
      4. eardrum
      5. phon