Skip to main content
Physics LibreTexts

16.5: Further Topics

  1. Last updated
  2. Save as PDF
  • Page ID
    14540
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    learning objectives

    • Identify sources of spherical and plane wave patterns

    Spherical Waves

    Christiaan Huygens was a Dutch scientist who developed a useful technique for determining how and where waves propagate. In 1678, he proposed that every point that a luminous disturbance touches becomes itself a source of a spherical wave; the sum of these secondary waves determines the form of the wave at any subsequent time. The Huygen-Fresnel Principle shows that as the waves interact with each other, they interfere either constructively or destructively. Constructive interference occurs when waves are completely in phase with each other and amplifies the waves. Destructive interference occurs when waves are exactly out of phase with either other, and if waves are perfectly out of phase with each other, the wave will be canceled out completely. Since the waves all come from one point source, the waves happen in a spherical pattern. All the waves come from a single point source and are spherical.

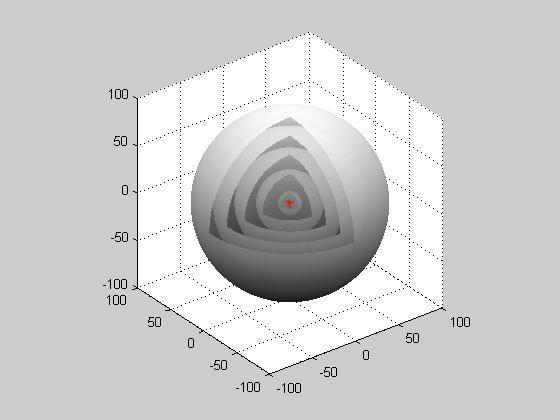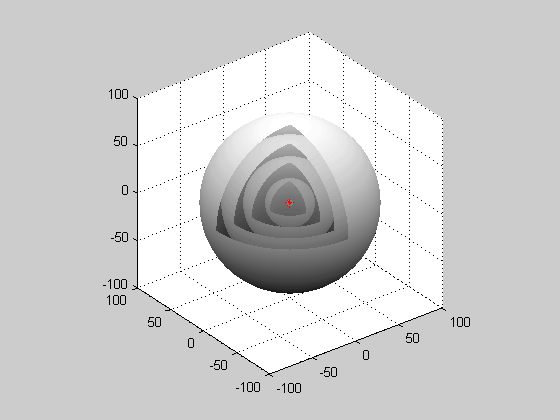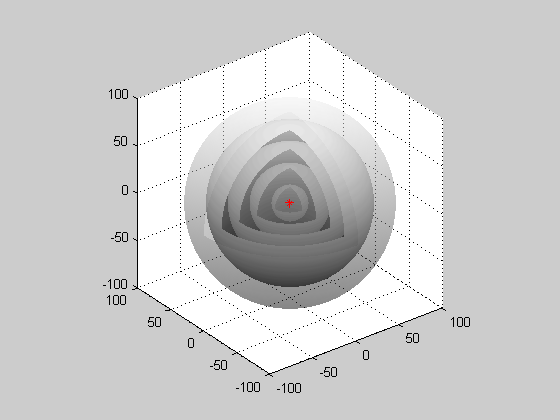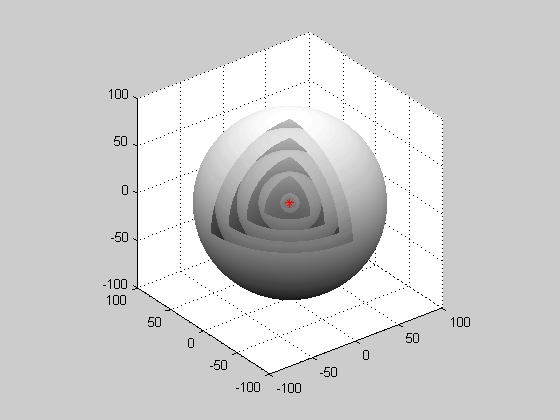
    image

    Spherical Wave: When waves are produced from a point source, they are spherical waves.

    image

    Huygen-Fresnel Principle: The Huygen-Fresnel Principle uses the law of refraction. Each point on the wave produces waves which interfere with each other either constructively or destructively.

    Plane Waves

    A plane wave is a constant-frequency wave whose wavefronts (surfaces of constant phase) are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector. It is not possible in practice to have a true plane wave; only a plane wave of infinite extent will propagate as a plane wave. However, many waves are approximately plane waves in a localized region of space. For example, a localized source such as an antenna produces a field that is approximately a plane wave far from the antenna in its far-field region. Similarly, if the length scales are much longer than the wave’s wavelength, as is often the case for light in the field of optics, one can treat the waves as light rays which correspond locally to plane waves.

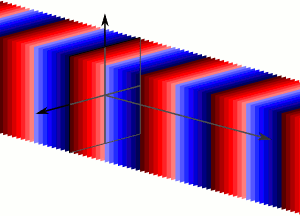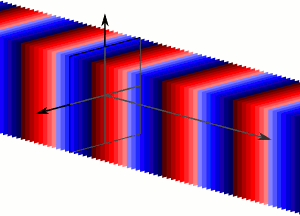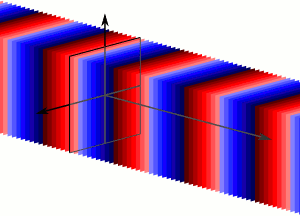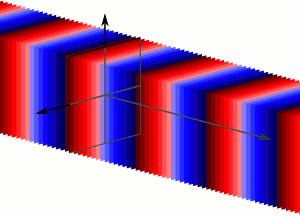
    image

    Plane Wave: Plane waves are an infinite number of wavefronts normal to the direction of the propogation.

    Standing Waves on a String

    Standing wave occurs due to the interference when transverse waves in strings are reflected and the incident and reflected waves meet.

    learning objectives

    • Identify when a standing wave occurs

    A standing wave is a wave that appears stationary, meaning it remains in a constant position. In a string, a standing wave is a type of transverse wave—where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. A standing wave can occur when two identical waves moving in different directions along the string interfere.

    There are two scenarios of waves in strings: the string is fixed at both ends, or the string is fixed at one end and free at the other. A transverse wave will move along the string until it reaches the other end. It is then reflected from that end and starts to move back towards the original direction; at this point interference occurs. shows a transverse wave that is reflected from a fixed end. When a transverse wave meets a fixed end, the wave is reflected, but inverted. This swaps the peaks with the troughs and the troughs with the peaks. diagrams a transverse wave on a string that meets a free end. The wave is reflected, but unlike a transverse wave with a fixed end, it is not inverted.

    image

    Free End Reflection: The wave is reflected, but unlike a transverse wave with a fixed end, it is not inverted.

    image

    Fixed End Reflection: When a transverse wave meets a fixed end, the wave is reflected, but inverted.

    Standing Waves

    When either of the two scenarios of wave reflection occurs, the incident wave meets the reflected wave. These waves move past each other in opposite directions, causing interference. When these two waves have the same frequency, the product of this is called the standing waves. Standing waves appear to be standing still, hence the name. illustrates a very slow moving standing wave. (One application of the principle of standing waves is in music with the concept of resonance—and how many musical instruments, like guitars and pianos, get their sound. ) Let us now examine how standing waves occur.

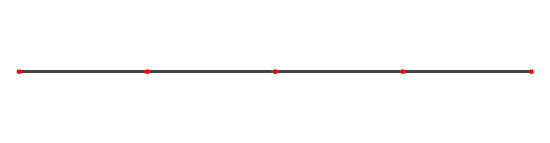
    image

    Standing Wave on a String: This is what a standing wave would look like if you were to slow it down. The wave is caused by an incident wave on a string being reflected and then traveling back in the direction it came from. The two waves then meet and interfere with each other causing this phenomenon.

    Constructive vs. Destructive Interference

    When the incident wave and reflected wave first meet, both waves have an amplitude is zero. As the waves continue to move past each other they continue to interfere with each other, either constructively of destructively. As discussed in previous atoms, when waves are completely in phase and interfere with each other constructively they are amplified, and when they are completely out of phase and interfere destructively they cancel out. As the waves continue to move past each other, and are reflected from the opposite end, they continue to interfere both ways; a standing wave is produced. Every point in the medium containing a standing wave oscillates up and down, and the amplitude of the oscillations depends on the location of the point. When we observe a standing wave on strings, it appears the wave is not moving but standing still. In summary:

    • The points which reach the maximum oscillation height are called antinodes, and are results of complete constructive interference.
    • The points in a standing wave that appear to remain flat and do not move are called nodes. These are due to complete destructive interference.

    Standing Waves in Air Columns

    Standing waves in air columns is the physical phenomenon that gives wind instruments their resonance and, therefore, sound.

    learning objectives

    • Identify the type of a standing wave in an air column

    Standing Waves

    A standing wave is a wave that appears to be stationary, meaning it remains in a constant position. In an air column, a standing wave can form as either a longitudinal or transverse wave. A transverse wave, you may remember, is a wave where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. A longitudinal wave, on the other hand, is parallel to the direction of propagation. A standing wave can occur when two identical waves moving in different directions interfere.

    Air Columns

    When a standing wave is formed in a tube, the standing wave has a maximum air displacement at the open end called an antinode. Here, the motion is unconstrained. At the closed end, there is no displacement; this is called a node, and the air is halted. The distance from a node to antinode is 1/4 of a wavelength, and is equal to the length of the tube.

    shows that this resonance can be produced by a vibration introduced at or near the closed end of the tube as well. This is considered to be a natural vibration of the air column independently of how it is induced. Given that maximum air displacements are possible at the open end and none at the closed end, there are other, shorter wavelengths that can resonate in the tube. For example, a standing wave can have three-fourths of its wavelength in the tube, or L=(3/4)λ. This can be rendered as follows:

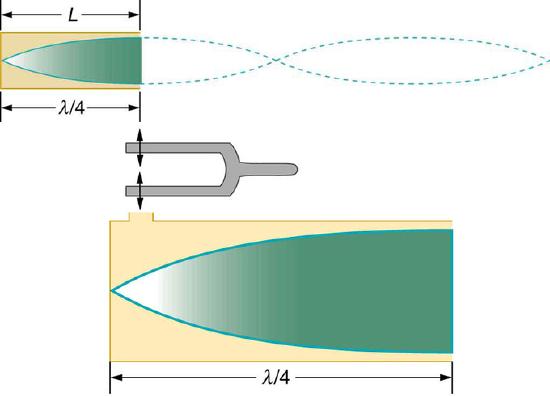
    image

    Standing Wave in Air Column: The same standing wave is created in the tube by a vibration introduced near its closed end.

    \[\lambda ^ { \prime } = \dfrac { 4 \mathrm { L } } { 3 }\]

    Continuing this process reveals a whole series of shorter-wavelength and higher-frequency sounds that resonate in the tube. We use specific terms for the resonances in any system. The lowest resonant frequency is called the fundamental, while all higher resonant frequencies are called overtones. All resonant frequencies are integral multiples of the fundamental, and they are collectively called harmonics. The fundamental is the first harmonic, the first overtone is the second harmonic, and so on. shows hows the fundamental and the first three overtones (the first four harmonics) in a tube closed at one end.

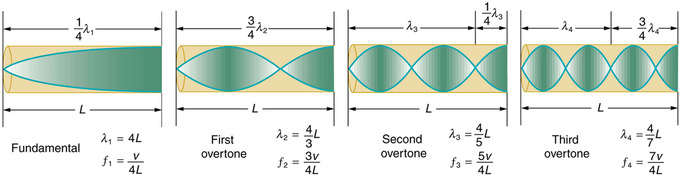
    image

    The First Four Harmonics: The fundamental and three lowest overtones for a tube closed at one end. All have maximum air displacements at the open end and none at the closed end.

    Now let us look for a pattern in the resonant frequencies for a simple tube that is closed at one end. The fundamental has =4L, and frequency is related to wavelength and the speed of sound as given by the following:

    \[\mathbf { v } _ { \mathrm { w } } = \mathrm { f } \lambda\]

    Solving for f in this equation gives a more helpful form:

    \[\mathrm { f } = \dfrac { \mathrm { v } _ { \mathrm { w } } } { \lambda } = \dfrac { \mathbf { v } _ { \mathrm { w } } } { 4 \mathrm { L } }\]

    Here, f is frequency, vw is speed of sound in air, λ is wavelength, and L is the length of the air column. The first overtone has = 4L/3. From this, we can deduce the following:

    \[\mathrm { f } ^ {\prime } = 3 \dfrac { v _ { \mathrm { w } } } { 4 \mathrm { L } } = 3 \mathrm { f }\]

    Because f′ = 3f, we call the first overtone the third harmonic. Continuing this process, we see a pattern that can be generalized in a single expression. The resonant frequencies of a tube closed at one end are:

    \[\mathrm { f } _ { \mathrm { n } } = \mathrm { n } \dfrac { \mathrm { vw } } { 4 \mathrm { L } } , \mathrm { n } = 1,3,5\]

    Here, f1 is the fundamental, f3 is the first overtone, and so on. It is interesting that the resonant frequencies depend on the speed of sound and, hence, on temperature. This dependence poses a noticeable problem for organs in old unheated cathedrals, and it is also the reason why musicians commonly bring their wind instruments to room temperature before playing them.

    Example \(\PageIndex{1}\):

    The fundamental and overtones can be present simultaneously in a variety of combinations. For example, middle C on a trumpet has a sound distinctively different from middle C on a clarinet, both instruments being modified versions of a tube closed at one end. The fundamental frequency is the same (and usually the most intense), but the overtones and their mix of intensities are different and subject to shading by the musician. This mix is what gives various musical instruments (and human voices) their distinctive characteristics, whether they have air columns, strings, sounding boxes, or drumheads. In fact, much of our speech is determined by shaping the cavity formed by the throat and mouth and positioning the tongue to adjust the fundamental and combination of overtones. Simple resonant cavities can be made to resonate with the sound of the vowels, for example.

    Forced Vibrations and Resonance

    The phenomenon of driving a system with a frequency equal to its natural frequency is called resonance.

    learning objectives

    • Explain the relationship between the resonance curve and damping

    Forced Vibration and Resonance

    Many people have played with toys involving an object supported by an elastic band: something like the paddle ball suspended from a finger in. Say a person drives the paddle ball by moving his or her finger up and down at a certain frequency. In this example, he or she is causing a forced oscillation (or vibration). At first the finger is held steady, and the ball bounces up and down with a small amount of damping. If the finger is moved up and down slowly, the ball will follow along without bouncing much on its own.

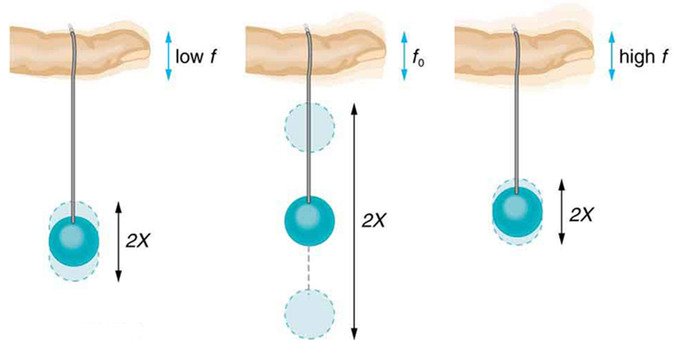
    image

    Paddle Balls and Frequencies: The paddle ball on its rubber band moves in response to the finger supporting it. If the finger moves with the natural frequency f0 of the ball on the rubber band, then a resonance is achieved, and the amplitude of the ball’s oscillations increases dramatically. At higher and lower driving frequencies, energy is transferred to the ball less efficiently, and it responds with lower-amplitude oscillations.

    As the frequency at which the finger is moved up and down increases, the ball will respond by oscillating with increasing amplitude. After driving the ball at its natural frequency, the ball’s oscillations increase in amplitude with each oscillation for as long as it is driven. The phenomenon of driving a system with a frequency equal to its natural frequency is called resonance. As the driving frequency gets progressively higher than the resonant or natural frequency, the amplitude of the oscillations becomes smaller until the oscillations nearly disappear and the finger simply moves up and down with little effect on the ball.

    Effects of Damping

    In real life, most oscillators have damping present in the system. It is interesting that the widths of the resonance curves shown in depend on damping: the less the damping, the narrower the resonance. For a driven oscillator to resonate at a very specific frequency, there needs to be as little damping as possible, as is the case for piano strings and many other musical instruments. Conversely, for small-amplitude oscillations, such as in a car’s suspension system, there needs to be heavy damping. Heavy damping reduces the amplitude, but the tradeoff is that the system responds at more frequencies.

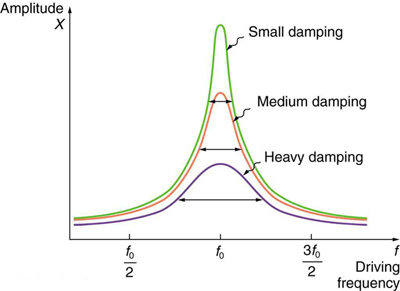
    image

    Damping: The amplitude of a harmonic oscillator is a function of the frequency of the driving force. The curves represent the same oscillator with the same natural frequency but with different amounts of damping. Resonance occurs when the driving frequency equals the natural frequency, and the greatest response is for the least amount of damping. The narrowest response is also for the least amount of damping.

    Example \(\PageIndex{2}\):

    These features of driven harmonic oscillators apply to a huge variety of systems. When tuning a radio, for example, people are adjusting the resonant frequency of the radio circuit so that it only oscillates to the desired station’s broadcast (or driving) frequency. The more selective the radio is in discriminating between stations, the smaller its damping. A child on a swing is driven by a parent at the swing’s natural frequency to achieve maximum amplitude. In all of these cases, the efficiency of energy transfer from the driving force into the oscillator is best at resonance. On gravel roads that are corrugated, if people travel at the ‘wrong’ speed, the bumps are very noticeable. At other speeds, it is difficult to feel the bumps at all. shows a photograph of a famous example (the Tacoma Narrows Bridge) of the destructive effects of a driven harmonic oscillation. Unfortunately, heavy winds happened to drive the bridge at its natural frequency, leading to the collapse.

    image

    Collapse of the Tacoma Narrows Bridge: In 1940, the Tacoma Narrows Bridge in Washington state collapsed. Heavy cross winds drove the bridge into oscillations at its resonant frequency. The damping decreased when support cables broke loose and started to slip over the towers, allowing increasingly greater amplitudes until the structure failed. (credit: PRI’s Studio 360, via Flickr)

    Key Points

    • The waves either interfere with each other constructively or destructively, which will either amplify or minimize the wave, respectively.
    • Spherical waves are emitted from a single point source in a spherical shape.
    • A plane wave is a constant-frequency wave whose wavefronts (surfaces of constant phase ) are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector.
    • Although it is not possible in practice to have a true plane wave, many waves approximate plane wave behavior.
    • The reflected wave is inverted from the incident wave when a transverse wave on a string is fixed at the end point. The reflected wave is not inverted from the incident wave when a transverse wave on a string is free at the end point.
    • A standing wave occurs when an incident wave meets a reflected wave on a string.
    • A standing wave contains nodes (points that remain flat due to the destructive interference ) and antinodes (points with maximum oscillation due to the constructive interference ).
    • Every point in the string oscillates up and down and the amplitude of the oscillations depends on the location of the point.
    • A standing wave has some points that remain flat due to destructive interference. These are called antinodes.
    • The points on a standing wave that have reached maximum oscillation do so from constructive interference, and are called nodes.
    • A standing wave in an air column is a transverse wave.
    • A node occurs at the closed end of an air tube where there is no wave displacement.
    • An antinode occurs at the open end of the air tube where the maximum displacement occurs.
    • The resonant frequencies of a tube closed at one end are as follows: \(\mathrm { f } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { vw } } { 4 \mathrm { L } }\), n=1,3,5.
    • Any oscillator has a natural frequency. Driven at the natural frequency, oscillations increase in amplitude with each oscillation.
    • The widths of the resonance curves depend on damping: less damping corresponds to a narrower resonance. With less damping, the resonance peak becomes more pronounced.
    • The relationship between resonance and damping applies to a huge variety of systems. Damping is often reduced or enhanced to induce the desired response of an oscillator.

    Key Terms

    • wavefront: An imaginary surface passing through points of a medium oscillating in phase.
    • destructive interference: Occurs when waves interfere with each other crest to trough (peak to valley) and are exactly out of phase with each other.
    • constructive interference: Occurs when waves interfere with each other crest to crest and the waves are exactly in phase with each other.
    • transverse wave: Any wave in which the direction of disturbance is perpendicular to the direction of travel.
    • natural frequency: The frequency at which a system vibrates on its own. For a spring (spring constant k) with an object of mass m attached, the natural frequency is given as \(\mathrm { f } _ { \mathrm { n } } = \frac { 1 } { 2 \pi } \sqrt { \frac { \mathrm { k } } { \mathrm { m } } }\).
    • damping: The reduction in the magnitude of oscillations by the dissipation of energy

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    This page titled 16.5: Further Topics is shared under a not declared license and was authored, remixed, and/or curated by Boundless.