Skip to main content
Physics LibreTexts

20.4: Voltmeters and Ammeters

  1. Last updated
  2. Save as PDF
  • Page ID
    14567
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    learning objectives

    • Compare circuit connection of an ammeter and a voltmeter

    Voltmeters and ammeters measure the voltage and current, respectively, of a circuit. Some meters in automobile dashboards, digital cameras, cell phones, and tuner-amplifiers are voltmeters or ammeters.

    Voltmeters and Ammeters: A brief introduction to voltmeters and ammeters for introductory physics students.

    Voltmeters

    A voltmeter is an instrument that measures the difference in electrical potential between two points in an electric circuit. An analog voltmeter moves a pointer across a scale in proportion to the circuit’s voltage; a digital voltmeter provides a numerical display. Any measurement that can be converted to voltage can be displayed on a meter that is properly calibrated; such measurements include pressure, temperature, and flow.

    image

    Voltmeter: Demonstration voltmeter from a physics class

    In order for a voltmeter to measure a device’s voltage, it must be connected in parallel to that device. This is necessary because objects in parallel experience the same potential difference.

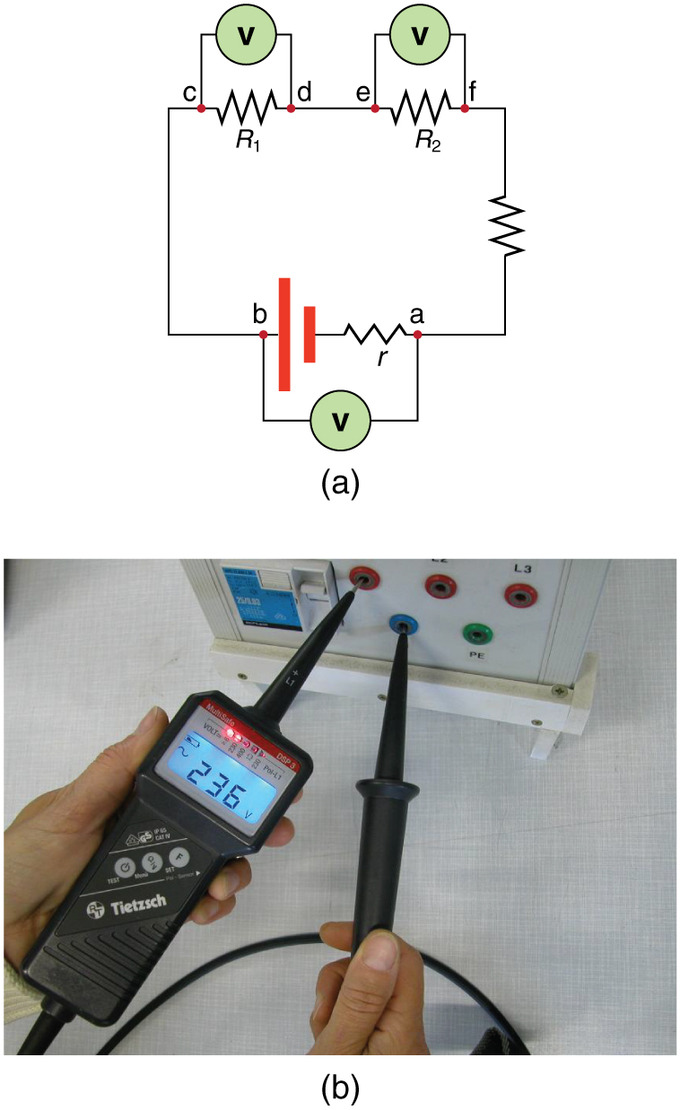
    image

    Voltmeter in Parallel: (a) To measure the potential difference in this series circuit, the voltmeter (V) is placed in parallel with the voltage source or either of the resistors. Note that terminal voltage is measured between points a and b. It is not possible to connect the voltmeter directly across the EMF without including its internal resistance, r. (b) A digital voltmeter in use

    Ammeters

    An ammeter measures the electric current in a circuit. The name is derived from the name for the SI unit for electric current, amperes (A).

    In order for an ammeter to measure a device’s current, it must be connected in series to that device. This is necessary because objects in series experience the same current. They must not be connected to a voltage source — ammeters are designed to work under a minimal burden, (which refers to the voltage drop across the ammeter, typically a small fraction of a volt).

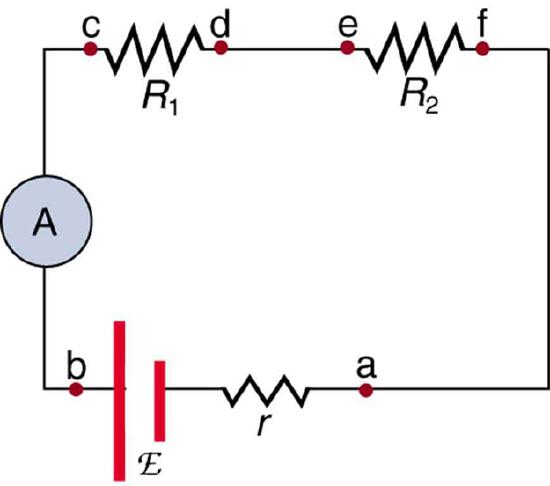
    image

    Ammeter in Series: An ammeter (A) is placed in series to measure current. All of the current in this circuit flows through the meter. The ammeter would have the same reading if located between points d and e or between points f and a, as it does in the position shown. (Note that the script capital E stands for EMF, and r stands for the internal resistance of the source of potential difference. )

    Galvanometers (Analog Meters)

    Analog meters have needles that swivel to point at numbers on a scale, as opposed to digital meters, which have numerical readouts.The heart of most analog meters is a device called a galvanometer, denoted by G. Current flow through a galvanometer, IG, produces a proportional movement, or deflection, of the needle.

    The two crucial characteristics of any galvanometer are its resistance and its current sensitivity. Current sensitivity is the current that gives a full-scale deflection of the galvanometer’s needle — in other words, the maximum current that the instrument can measure. For example, a galvanometer with a current sensitivity of 50 μA has a maximum deflection of its needle when 50 μA flows through it, is at the scale’s halfway point when 25 μA flows through it, and so on.

    If such a galvanometer has a 25-Ω resistance, then a voltage of only \(\mathrm{V = IR = (50 \mu A)(25 \Omega)=1.25 \; mV}\) produces a full-scale reading. By connecting resistors to this galvanometer in different ways, you can use it as either a voltmeter or ammeter to measure a broad range of voltages or currents.

    Galvanometers as Voltmeters

    A galvanometer can function as a voltmeter when it is connected in series with a large resistance R. The value of R is determined by the maximum voltage that will be measured. Suppose you want 10 V to produce a full-scale deflection of a voltmeter containing a 25-Ω galvanometer with a 50-μA sensitivity. Then 10 V applied to the meter must produce a current of 50 μA. The total resistance must be:

    \[\mathrm { R } _ { \mathrm { tot } } = \mathrm { R } + \mathrm { r } = \dfrac { \mathrm { V } } { \mathrm { I } } = \frac { 10 \mathrm { V } } { 50 \mu \mathrm { A } } = 200 \mathrm { k } \Omega\]

    or:

    \[\mathrm { R } = \mathrm { R } _ { \mathrm { tot } } - \mathrm { r } = 200 \mathrm { k } \Omega - 25 \Omega \approx 200 \mathrm { k } \Omega\]

    (R is so large that the galvanometer resistance, r, is nearly negligible. ) Note that 5 V applied to this voltmeter produces a half-scale deflection by sending a 25-μA current through the meter, and so the voltmeter’s reading is proportional to voltage, as desired. This voltmeter would not be useful for voltages less than about half a volt, because the meter deflection would be too small to read accurately. For other voltage ranges, other resistances are placed in series with the galvanometer. Many meters allow a choice of scales, which involves switching an appropriate resistance into series with the galvanometer.

    Galvanometers as Ammeters

    The same galvanometer can also function as an ammeter when it is placed in parallel with a small resistance R, often called the shunt resistance. Since the shunt resistance is small, most of the current passes through it, allowing an ammeter to measure currents much greater than those that would produce a full-scale deflection of the galvanometer.

    Suppose, for example, we need an ammeter that gives a full-scale deflection for 1.0 A and that contains the same 25-Ω galvanometer with 50-μA sensitivity. Since R and r are in parallel, the voltage across them is the same.

    These IR drops are: IR = IGr

    so that: \(\mathrm { IR } = \frac { \mathrm { I } _ { \mathrm { G } } } { \mathrm { I } } = \frac { \mathrm { R } } { \mathrm { r } }\).

    Solving for R, and noting that IG is 50 μA and I is 0.999950 A, we have:

    \[\mathrm { R } = \mathrm { r } \frac { \mathrm { I } _ { \mathrm { G } } } { \mathrm { I } } = ( 25 \Omega ) \frac { 50 \mu \mathrm { A } } { 0.999950 \mathrm { A } } = 1.25 \times 10 ^ { - 3 } \Omega\]

    Null Measurements

    Null measurements balance voltages so there is no current flowing through the measuring devices that would interfere with the measurement.

    learning objectives

    • Explain why null measurements are employed

    Null Measurements

    Standard measurements of voltage and current alter circuits, introducing numerical uncertainties. Voltmeters draw some extra current, whereas ammeters reduce current flow. Null measurements balance voltages, so there is no current flowing through the measuring device and the circuit is unaltered. Null measurements are generally more accurate but more complex than standard voltmeters and ammeters. Their precision is still limited.

    The Potentiometer

    When measuring the EMF of a battery and connecting the battery directly to a standard voltmeter, as shown in, the actual quantity measured is the terminal voltage V. Voltage is related to the EMF of the battery by V=emf−Ir, where I is the current that flows and r is the internal resistance of the battery.

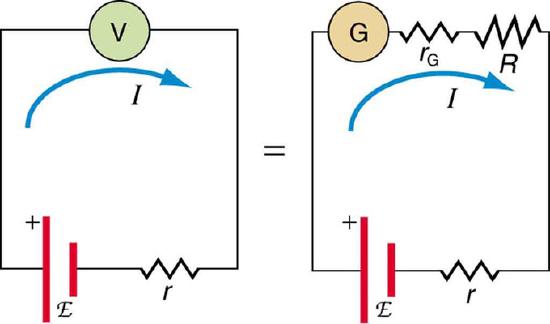
    image

    Voltmeter Connected to Battery: An analog voltmeter attached to a battery draws a small but nonzero current and measures a terminal voltage that differs from the EMF of the battery. (Note that the script capital E symbolizes electromotive force, or EMF. ) Since the internal resistance of the battery is not known precisely, it is not possible to calculate the EMF precisely.

    The EMF could be accurately calculated if r were known, which is rare. If the current I could be made zero, then V=emf, and EMF could be directly measured. However, standard voltmeters need a current to operate.

    A potentiometer is a null measurement device for measuring potentials (voltages). A voltage source is connected to resistor R, passing a constant current through it. There is a steady drop in potential (IR drop) along the wire, so a variable potential is obtained through contact along the wire.

    An unknown emfx (represented by script Ex) connected in series with a galvanometer is shown in. Note that emfx opposes the other voltage source. The location of the contact point is adjusted until the galvanometer reads zero. When the galvanometer reads zero, emfx=IRx, where Rxis the resistance of the wire section up to the contact point. Since no current flows through the galvanometer, none flows through the unknown EMF, and emfx is sensed.

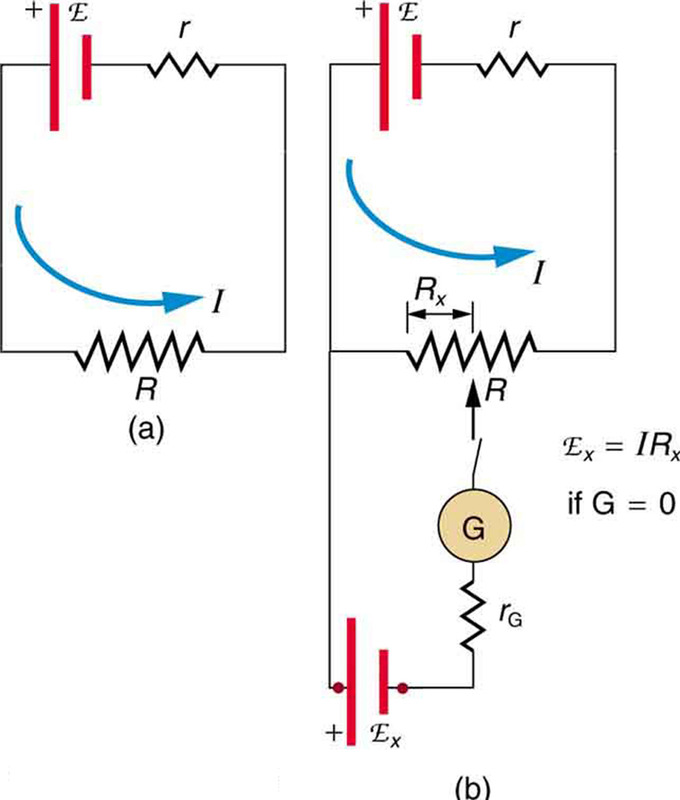
    image

    Potentiometer: The potentiometer is a null measurement device. (a. ) A voltage source connected to a long wire resistor passes a constant current I through it. (b.) An unknown EMF (labeled script Ex) is connected as shown, and the point of contact along R is adjusted until the galvanometer reads zero. The segment of wire has a resistance Rx and script Ex=IRx, where I is unaffected by the connection, since no current flows through the galvanometer. The unknown EMF is thus proportional to the resistance of the wire segment.

    Standard EMF is substituted for emfx, and the contact point is adjusted until the galvanometer reads zero, so that emfs=IRs. In both cases, no current passes through the galvanometer. The current Ithrough the long wire is identical. Taking the ratio emfx/emfs, Icancels, and solving for emfx gives what is seen in.

    Because a long uniform wire is used for R, the ratio of resistances Rx/Rs is the same as the ratio of the lengths of wire that zero the galvanometer for each EMF. The three quantities on the right-hand side of the equation are now known or measured, and emfx can be calculated. There is often less uncertainty in this calculation than when using a voltmeter directly, but it is not zero. There is always some uncertainty in the ratio of resistances Rx/Rsand in the standard EMFs. Furthermore, it is not possible to tell when the galvanometer reads exactly zero, which introduces error into both Rx and Rs, and may also affect the current I.

    Resistance Measurements

    Many so-called ohmmeters measure resistance. Most common ohmmeters apply a voltage to a resistance, measure the current, and calculate the resistance using Ohm ‘s law. Their readout is this calculated resistance. Simple configurations using standard voltmeters and ammeters have limited accuracy, because the meters alter both the voltage applied to the resistor and the current flowing through it. The Wheatstone bridge is a null measurement device for calculating resistance by balancing potential drops in a circuit. The device is called a bridge because the galvanometer forms a bridge between two branches. A variety of bridge devicesare used to make null measurements in circuits. Resistors R1 and R2 are precisely known, while the arrow through R3indicates that it is a variable resistance. The value of R3 can be precisely read. With the unknown resistance Rx in the circuit, R3 is adjusted until the galvanometer reads zero.

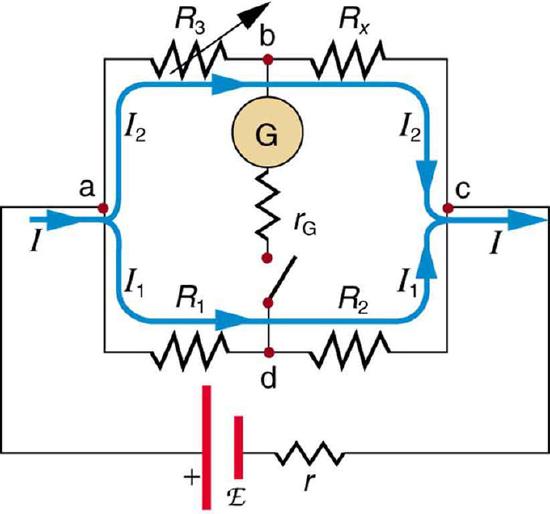
    image

    Wheatstone Bridge: The Wheatstone bridge is used to calculate unknown resistances. The variable resistance R3 is adjusted until the galvanometer reads zero with the switch closed. This simplifies the circuit, allowing Rx to be calculated based on the IR drops.

    The potential difference between points b and d is then zero, meaning that b and d are at the same potential. With no current running through the galvanometer, it has no effect on the rest of the circuit. So the branches abc and adc are in parallel, and each branch has the full voltage of the source. Since b and d are at the same potential, the IR drop along ad must equal the IR drop along ab. Again, since b and d are at the same potential, the IR drop along dcmust equal the IR drop along bc. This equation is used to calculate the unknown resistance when current through the galvanometer is zero. This method can be very accurate, but it is limited by two factors. First, it is not possible for the current through the galvanometer to be exactly zero. Second, there are always uncertainties in R1, R2, and R3, which contribute to the uncertainty in Rx.

    Key Points

    • A voltmeter is an instrument used for measuring electrical potential difference between two points in an electric circuit.
    • An ammeter is a measuring device used to measure the electric current in a circuit.
    • A voltmeter is connected in parallel with a device to measure its voltage, while an ammeter is connected in series with a device to measure its current.
    • At the heart of most analog meters is a galvanometer, an instrument that measures current flow using the movement, or deflection, of a needle. The needle deflection is produced by a magnetic force acting on a current-carrying wire.
    • Measurements of voltages and current with standard voltmeters and ammeters alter the circuit being measured, introducing uncertainties. Voltmeters draw some extra current, whereas ammeters reduce current flow.
    • Null measurements are employed to reduce the uncertainty in the measured voltage and current.
    • The potentiometer and the Wheatstone bridge are two methods for making null measurements.
    • The potentiometer is an instrument that measures an unknown voltage by opposing with a known voltage, without drawing current from the voltage source being measured.
    • A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component.

    Key Terms

    • shunt resistance: a small resistance R placed in parallel with a galvanometer G to produce an ammeter; the larger the current to be measured, the smaller R must be; most of the current flowing through the meter is shunted through R to protect the galvanometer
    • galvanometer: An analog measuring device, denoted by G, that measures current flow using a needle deflection caused by a magnetic field force acting upon a current-carrying wire.
    • null measurements: methods of measuring current and voltage more accurately by balancing the circuit so that no current flows through the measurement device
    • potentiometer: an instrument that measures a voltage by opposing it with a precise fraction of a known voltage, and without drawing current from the unknown source.
    • Wheatstone bridge: An instrument used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component.

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    This page titled 20.4: Voltmeters and Ammeters is shared under a not declared license and was authored, remixed, and/or curated by Boundless.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      Boundless
      Show TOC
      no
    2. Tags
      1. galvanometer
      2. null measurements
      3. potentiometer
      4. Shunt resistance
      5. Wheatstone bridge