21.3: Magnetic Force on a Moving Electric Charge
( \newcommand{\kernel}{\mathrm{null}\,}\)
Magnitude of the Magnetic Force
How does one magnet attracts another? The answer relies on the fact that all magnetism relies on current, the flow of charge. Magnetic fields exert forces on moving charges, and so they exert forces on other magnets, all of which have moving charges.
The magnetic force on a moving charge is one of the most fundamental known. The magnetic force is as important as the electrostatic or Coulomb force. Yet the magnetic force is more complex, in both the number of factors that affects it and in its direction, than the relatively simple Coulomb force. The magnitude of the magnetic force F on a charge q moving at a speed v in a magnetic field of strength B is given by:
F=qvBsin(θ)
where θ is the angle between the directions of v and B. This formula is used to define the magnetic strength B in terms of the force on a charged particle moving in a magnetic field. The SI unit for magnitude of the magnetic field strength is called the tesla (T) in honor of the brilliant and eccentric inventor Nikola Tesla (1856–1943), who made great contributions to our understanding of magnetic fields and their practical applications. To determine how the tesla relates to other SI units, we solve F=qvBsin(θ) for B:
B=Fqvsin(θ)
Because sinθ is unitless, the tesla is
1T=1NC×m/s=1NA×m
Another smaller unit, called the gauss (G), where 1 G=10−4 T, is sometimes used. The strongest permanent magnets have fields near 2 T; superconducting electromagnets may attain 10 T or more. The Earth’s magnetic field on its surface is only about 5×10−5 T, or 0.5 G.
The direction of the magnetic force F is perpendicular to the plane formed by v and B as determined by the right hand rule, which is illustrated in Figure 1. It states that, to determine the direction of the magnetic force on a positive moving charge, you point the thumb of the right hand in the direction of v, the fingers in the direction of B, and a perpendicular to the palm points in the direction of F. One way to remember this is that there is one velocity, and so the thumb represents it. There are many field lines, and so the fingers represent them. The force is in the direction you would push with your palm. The force on a negative charge is in exactly the opposite direction to that on a positive charge.
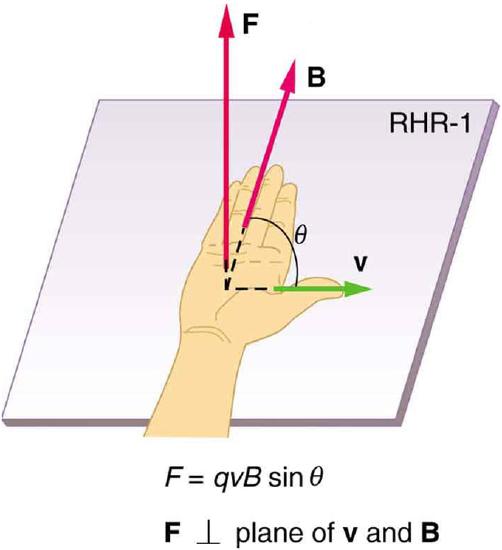
Right Hand Rule: Magnetic fields exert forces on moving charges. This force is one of the most basic known. The direction of the magnetic force on a moving charge is perpendicular to the plane formed by v and B and follows right hand rule–1 (RHR-1) as shown. The magnitude of the force is proportional to q, v, B, and the sine of the angle between v and B.
Direction of the Magnetic Force: The Right Hand Rule
The right hand rule is used to determine the direction of the magnetic force on a positive charge.
learning objectives
- Apply the right hand rule to determine the direction of the magnetic force on a charge
Direction of the Magnetic Force: The Right Hand Rule
So far we have described the magnitude of the magnetic force on a moving electric charge, but not the direction. The magnetic field is a vector field, thus the force applied will be oriented in a particular direction. There is a clever way to determine this direction using nothing more than your right hand. The direction of the magnetic force F is perpendicular to the plane formed by v and B, as determined by the right hand rule, which is illustrated in the figure above. The right hand rule states that: to determine the direction of the magnetic force on a positive moving charge, ƒ, point the thumb of the right hand in the direction of v, the fingers in the direction of B, and a perpendicular to the palm points in the direction of F.
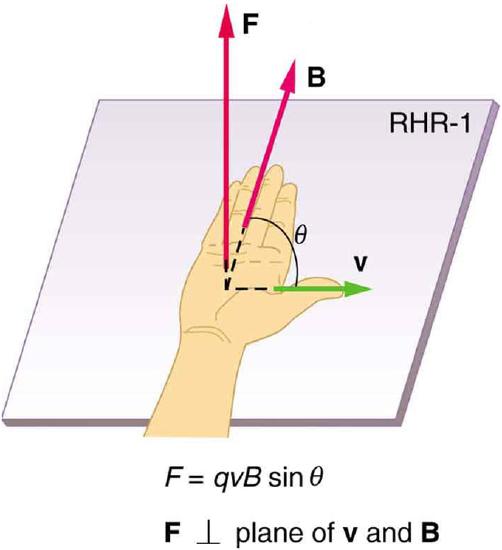
Right Hand Rule: Magnetic fields exert forces on moving charges. This force is one of the most basic known. The direction of the magnetic force on a moving charge is perpendicular to the plane formed by v and B and follows right hand rule–1 (RHR-1) as shown. The magnitude of the force is proportional to q, v, B, and the sine of the angle between v and B.
One way to remember this is that there is one velocity, represented accordingly by the thumb. There are many field lines, represented accordingly by the fingers. The force is in the direction you would push with your palm. The force on a negative charge is in exactly the opposite direction to that on a positive charge. Because the force is always perpendicular to the velocity vector, a pure magnetic field will not accelerate a charged particle in a single direction, however will produce circular or helical motion (a concept explored in more detail in future sections). It is important to note that magnetic field will not exert a force on a static electric charge. These two observations are in keeping with the rule that magnetic fields do no work.
Key Points
- Magnetic fields exert forces on charged particles in motion.
- The direction of the magnetic force F is perpendicular to the plane formed by v and B as determined by the right hand rule.
- The SI unit for magnitude of the magnetic field strength is called the tesla (T), which is equivalent to one Newton per ampere-meter. Sometimes the smaller unit gauss (10-4 T) is used instead.
- When the expression for the magnetic force is combined with that for the electric force, the combined expression is known as the Lorentz force.
- When considering the motion of a charged particle in a magnetic field, the relevant vectors are the magnetic field B, the velocity of the particle v, and the magnetic force exerted on the particle F. These vectors are all perpendicular to each other.
- The right hand rule states that, to find the direction of the magnetic force on a positive moving charge, the thumb of the right hand point in the direction of v, the fingers in the direction of B, and the force (F) is directed perpendicular to the right hand palm.
- The direction of the force F on a negative charge is in the opposite sense to that above (so pointed away from the back of your hand).
Key Terms
- Coulomb force: the electrostatic force between two charges, as described by Coulomb’s law
- magnetic field: A condition in the space around a magnet or electric current in which there is a detectable magnetic force, and where two magnetic poles are present.
- tesla: In the International System of Units, the derived unit of magnetic flux density or magnetic inductivity. Symbol: T
- right hand rule: Direction of angular velocity ω and angular momentum L in which the thumb of your right hand points when you curl your fingers in the direction of rotation.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- magnetic field. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/magnetic_field. License: CC BY-SA: Attribution-ShareAlike
- Magnetic force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Magnetic_force. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42372/latest/?collection=col11406/1.7. License: CC BY: Attribution
- tesla. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/tesla. License: CC BY-SA: Attribution-ShareAlike
- Coulomb force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Coulomb_force. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42372/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42372/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Magnetic force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Magnetic_force. License: CC BY-SA: Attribution-ShareAlike
- Right hand rule. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Right_hand_rule. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/right-hand-rule. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42372/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 14, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42372/latest/?collection=col11406/1.7. License: CC BY: Attribution

