22.4: Magnetic Fields and Maxwell Revisited
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe behavior of an inductor when the current is changed, and express energy stored in a magnetic field in a form of equation
When a conductor carries a current, a magnetic field surrounding the conductor is produced. The resulting magnetic flux is proportional to the current. If the current changes, the change in magnetic flux is proportional to the time-rate of change in current by a factor called inductance (L). Since nature abhors rapid change, a voltage (electromotive force , EMF) produced in the conductor opposes the change in current, which is also proportional to the change in magnetic flux. Thus, inductors oppose change in current by producing a voltage that,in turn, creates a current to oppose the change in magnetic flux; the voltage is proportional to the change in current.
Energy Stored in Inductor
Due to energy conservation, the energy needed to drive the original current must have an outlet. For an inductor, that outlet is the magnetic field—the energy stored by an inductor is equal to the work needed to produce a current through the inductor. The formula for this energy is given as:
\mathrm { E } = \frac { 1 } { 2 } \mathrm { LI } ^ { 2 }
(Eq. 1), where L is the inductance in units of Henry and I is the current in units of Ampere.
Energy Stored in Magnetic Field
Let’s consider Fig 1, an example of a solenoid (ℓ: length, N: number of turns, I: current, A: cross-section area) that works as an inductor. From Eq. 1, the energy stored in the magnetic field created by the solenoid is:

Magnetic Field Created By A Solenoid: Magnetic field created by a solenoid (cross-sectional view) described using field lines. Energy is “stored” in the magnetic field.
\mathrm { E } = \dfrac { 1 } { 2 } \mathrm { L } \mathrm { I } ^ { 2 } = \dfrac { 1 } { 2 } \dfrac { \mu \mathrm { N } ^ { 2 } \mathrm { A } } { \mathrm { L } } \dfrac { \mathrm { B } ^ { 2 } \mathrm { L } ^ { 2 } } { \mu ^ { 2 } \mathrm { N } ^ { 2 } } = \dfrac { \mathrm { B } ^ { 2 } } { 2 \mu } \mathrm { AL }
(We used the relation \mathrm { L } = \frac { \mu \mathrm { I } ^ { 2 } \mathrm { A } } { 1 } and B=μNI/LB=μNI/L. )
Therefore, the energy density \mathrm{uB=energy/volume} of a magnetic field B is written as \mathrm { B } = \mu \mathrm { NI } / \mathrm { L }μ.
Maxwell’s Predictions and Hertz’ Confirmation
Maxwell’s prediction of the electromagnetic force was confirmed by Hertz who generated and detected electromagnetic waves.
learning objectives
- Explain how Maxwell’s prediction of the electromagnetic force was confirmed by Hertz
Maxwell’s Predictions and Hertz’ Confirmation
Combining the work of physicists including Oersted, Coulomb, Gauss, and Faraday, and adding his own insights, James Clerk Maxwell developed a complete and overarching theory showing electric and magnetic forces are not separate, but different forms of the same thing: the electromagnetic force. In 1865, he did this in the form of four equations that state the following:
- Electric field lines originate on positive charges and terminate on negative charges, and the electric field is defined as the force per unit charge on a test charge. The strength of the force is related to the electric constant ε0, also known as the permitivity of free space.
- Magnetic field lines are continuous, having no beginning or end. No magnetic monopoles are known to exist.
- A changing magnetic field induces an electromotive force (emf) and, hence, an electric field. The direction of the emf opposes the change.
- Magnetic fields are generated by moving charges or by changing electric fields.
Maxwell’s equations predict that regardless of wavelength and frequency, every light wave has the same structure. This means Maxwell’s equations predicted that radio and x-ray waves existed, even though they hadn’t actually been discovered yet.
Proving Maxwell’s Equations
Simple and brilliant in their insight, Maxwell’s famous equations would still be hard to prove. Since changing electric fields create relatively weak magnetic fields, they could not be easily detected at the time of Maxwell’s hypothesis.
It was not until 1888 that Maxwell’s prediction passed an important test when Heinrich Hertz generated and detected certain types of electromagnetic waves in the laboratory. He performed a series of experiments that not only confirmed the existence of electromagnetic waves, but also verified that they travel at the speed of light.
Hertz used an AC RLC (resistor-inductor-capacitor) circuit that resonates at a known frequency and connected it to a loop of wire as shown in. High voltages induced across the gap in the loop produced sparks that were visible evidence of the current in the circuit and that helped generate electromagnetic waves. Across the laboratory, Hertz had another loop attached to another RLC circuit, which could be tuned (as the dial on a radio) to the same resonant frequency as the first and could, thus, be made to receive electromagnetic waves. This loop also had a gap across which sparks were generated, giving solid evidence that electromagnetic waves had been received.
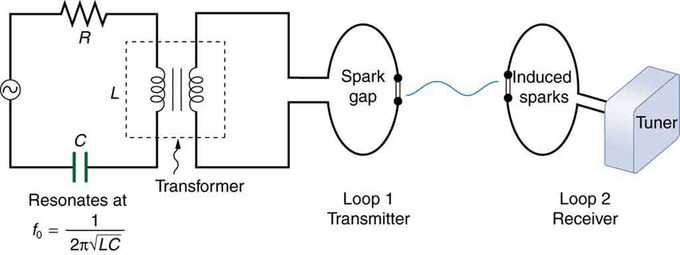
Apparatus Used by Hertz: The apparatus used by Hertz in 1887 to generate and detect electromagnetic waves. An RLC circuit connected to the first loop caused sparks across a gap in the wire loop and generated electromagnetic waves. Sparks across a gap in the second loop located across the laboratory gave evidence that the waves had been received.
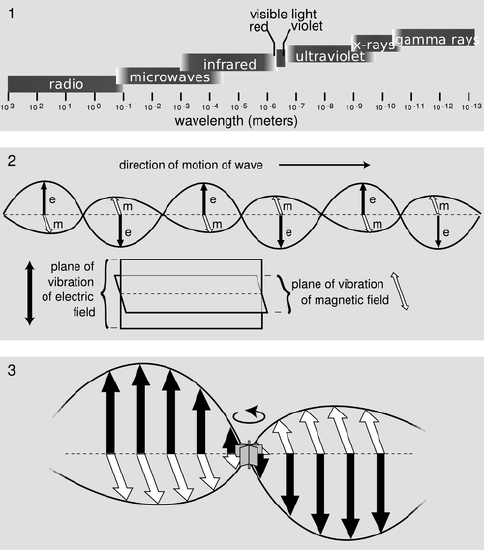
EM Wave: The propogation of an electromagnetic wave as predicted by Maxwell and confirmed by Hertz.
Key Points
- The formula for the energy stored in a magnetic field is E = 1/2 LI2.
- The energy stored in a magnetic field is equal to the work needed to produce a current through the inductor.
- Energy is stored in a magnetic field. Energy density can be written as \mathrm { u } _ { \mathrm { B } } = \frac { \mathrm { B } ^ { 2 } } { 2 \mu }.
- Maxwell predicted that electric and magnetic forces are linked.
- Maxwell’s equations predict that regardless of wavelength and frequency, every light wave has the same structure.
- Hertz was able to confirm Maxwell’s equation experimentally by generating and detecting certain types of electromagnetic waves in the laboratory.
Key Terms
- inductor: A device or circuit component that exhibits significant self-inductance; a device which stores energy in a magnetic field.
- electric field: A region of space around a charged particle, or between two voltages; it exerts a force on charged objects in its vicinity.
- magnetic field: A condition in the space around a magnet or electric current in which there is a detectable magnetic force, and where two magnetic poles are present.
- electromotive force: (EMF)—The voltage generated by a battery or by the magnetic force according to Faraday’s Law. It is measured in units of volts, not newtons, and thus, is not actually a force.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Fields. Provided by: Light and Matter. Located at: http://www.lightandmatter.com/html_books/7cp/ch06/ch06.html#Section6.2. License: CC BY-SA: Attribution-ShareAlike
- Inductor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Inductor. License: CC BY-SA: Attribution-ShareAlike
- Inductor. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Inductor. License: CC BY-SA: Attribution-ShareAlike
- inductor. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/inductor. License: CC BY-SA: Attribution-ShareAlike
- Solenoid. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Solenoid. License: CC BY: Attribution
- magnetic field. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/magnetic+field. License: CC BY-SA: Attribution-ShareAlike
- electric field. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electric+field. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42437/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42437/latest/?collection=col11406/latest. License: CC BY: Attribution
- electromotive force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/electromotive%20force. License: CC BY-SA: Attribution-ShareAlike
- Solenoid. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Solenoid. License: CC BY: Attribution
- Provided by: Light and Matter. Located at: http://www.lightandmatter.com/html_books/7cp/ch06/figs/emspectrum.png. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Maxwellu2019s Equations: Electromagnetic Waves Predicted and Observed. March 1, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42437/latest/Figure%2025_01_02a.jpg. License: CC BY: Attribution

