14.9: Problems

1. An alternate way to modify the energy-momentum relation while maintaining relativistic invariance is with a “potential mass”, \(H(x)\): \[ E^{2}=p^{2} c^{2}+(m+H)^{2} c^{4}\]

   If \(|H| \ll m \text { and } p^{2} \ll m^{2} c^{2}\), show how this equation may be approximated as \[ E=\text { something }+p^{2} /(2 m)\] and determine the form of “\(something\) ” in terms of \(H\). Is this theory distinguishable from the theory involving potential energy at nonrelativistic velocities?

2. For a given channel length \(L\) and particle speed in figure 14.1, determine the possible values of potential momentum \(\pm Q\) in the two channels that result in destructive interference between the two parts of the particle wave.
3. Show that equations (14.14) and (14.15) are indeed recovered from equations (14.12) and (14.13) when \(Q\) points in the \(y \) direction and is a function only of \(x\).
4. Show that the force \(F\) = \(v\) × \(P\) is perpendicular to the velocity \(v\). Does this force do any work on the particle? Is this consistent with the fact that the force doesn’t change the particle’s kinetic energy?
5. Show that the potential momentum illustrated in figure 14.2 satisfies the Lorenz condition, assuming that \(U \) = 0. Would the Lorenz condition be satisfied in this case if \(Q\) depended only on \(x \) and pointed in the \(x\) direction?
6. A mass \(m \) moves at non-relativistic speed around a circular track of radius \(R \) as shown in figure 14.7. The mass is subject to a potential momentum vector of magnitude \(Q \) pointing counterclockwise around the track.
   1. If the particle moves at speed \(v\), does it have a longer wavelength when it is moving clockwise or counterclockwise? Explain.
   2. Quantization of angular momentum is obtained by assuming that an integer number of wavelengths \(n \) fits into the circumference of the track. For given |\(n\) |, determine the speed of the mass (i) if it is moving clockwise (\(n < \) 0), and (ii) if it is moving counterclockwise (\(n > \) 0).
   3. Determine the kinetic energy of the mass as a function of \(n\).

   

   Figure 14.7: The particle is constrained to move along the illustrated track under the influence of a potential momentum \(Q\).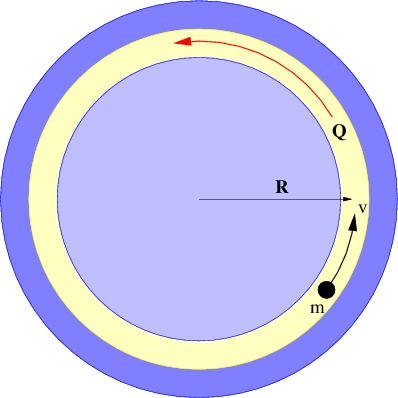
7. Suppose momentum were conserved for action at a distance in a particular reference frame between particles 1 cm apart as in the left panel of figure 14.4 in the text. If you are moving at velocity 2 × 10⁸ m s^-1 relative to this reference frame, for how long a time interval is momentum apparently not conserved? Hint: The 1 cm interval is the invariant distance between the kinks in the world lines.
8. An electron moving to the right at speed \(v \) collides with a positron (an antielectron) moving to the left at the same speed as shown in figure 14.8. The two particles annihilate, forming a virtual photon, which then decays into a proton-antiproton pair. The mass of the electron is \(m \) and the mass of the proton is \(M \) = 1830\(m\).
   1. What is the mass of the virtual photon? Hint: It is not 2\(m\). Why?
   2. What is the maximum possible lifetime of the virtual photon by the uncertainty principle?
   3. What is the minimum \(v \) the electron and positron need to have to make this reaction energetically possible? Hint: How much energy must exist in the proton-antiproton pair?

   

   Figure 14.8: Electron-positron annihilation leading to proton-antiproton production.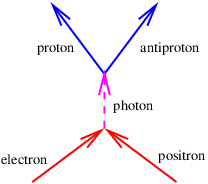
9. A muon (mass \(m\) ) interacts with a proton as shown in figure 14.9, so that the velocity of the muon before the interaction is \(v\), while after the interaction it is \(-v / 2\), all in the \(x\) direction. The interaction is mediated by a single virtual photon. Assume that \(v \ll c\) for simplicity.
   1. What is the momentum of the photon?
   2. What is the energy of the photon?

   

   Figure 14.9: Collision of a muon with a proton, mediated by the exchange of a virtual photon.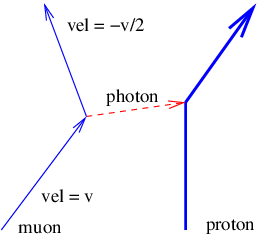
10. A photon with energy \(E \) and momentum \(E / c\) collides with an electron with momentum \(p=-E / c\) in the \(x \) direction and mass \(m\). The photon is absorbed, creating a virtual electron. Later the electron emits a photon in the \(x\) direction with energy \(E \) and momentum -\(E ∕ c\). (This process is called Compton scattering and is illustrated in figure 14.10.)
    1. Compute the energy of the electron before it absorbs the photon.
    2. Compute the mass of the virtual electron, and hence the maximum proper time it can exist before emitting a photon.
    3. Compute the velocity of the electron before it absorbs the photon.
    4. Using the above result, compute the energies of the incoming and outgoing photons in a frame of reference in which the electron is initially at rest. Hint: Using \(E_{\text {photon }}=\hbar \omega\) and the above velocity, use the Doppler shift formulas to get the photon frequencies, and hence energies in the new reference frame.

    

    Figure 14.10: Compton scattering.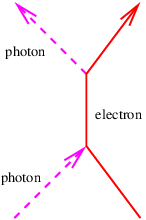
11. The dispersion relation for a negative energy relativistic particle is \[\omega=-\left(k^{2} c^{2}+\mu^{2}\right)^{1 / 2}\]

    Compute the group velocity of such a particle. Convert the result into an expression in terms of momentum rather than wavenumber. Compare this to the corresponding expression for a positive energy particle and relate it to Feynman’s explanation of negative energy states.

12. The potential energy of a charged particle in a scalar electromagnetic potential \(ϕ\) is the charge times the scalar potential. The total energy of such a particle at rest is therefore \[ E=\pm m c^{2}+q \phi \]

    where \(q \) is the charge on the particle and \(\pm m c^{2}\) is the rest energy, with the ± corresponding to positive and negative energy states. Assume that \(|q \phi| \ll m c^{2}\).

    1. Given that a particle with energy \(E<0\) is equivalent to the corresponding antiparticle with energy equal to \(-E>0\), what is the potential energy of the antiparticle?
    2. From this, what can you conclude about the charge on the antiparticle?

    Hint: Recall that the total energy is always rest energy plus kinetic energy (zero in this case) plus potential energy.