22.4: Problems

1. The George Washington bridge, which spans the Hudson River between New York and New Jersey, is 4760 feet long and is made out of steel. How much does it expand in length between winter and summer? (Pick reasonable winter and summer temperatures.)
2. A volume coefficient of expansion \(\beta\) can be defined for solids as well as liquids. Show that \(\beta=3 a\) in this case, where α is the linear coefficient of expansion. Hint: Imagine a cube that increases the length of a side by a fractional amount \(\alpha \Delta \mathrm{T} \ll 1\) when the temperature increases by \(\Delta \mathrm{T}\). Compute the fractional change in the volume of the cube.
3. Equal masses of brass and glass are put in the same insulating container, the brass initially at 300 K, the glass at 350 K. Assuming that the interior of the container has negligible heat capacity, what temperature does the material in the container reach after coming to equilibrium?
4. The gravitational potential energy of water going over Niagara Falls (60 m high) is converted to kinetic energy in the fall and then dissipated at the bottom. How much warmer does the water get as a result?
5. A normal-sized house has concrete walls and roof 0.1 m thick. About how much does it cost per month to heat the house electrically if electricity costs $0.10 per kilowatt-hour? Estimate the wall and roof areas of a typical house and typical inside-outside temperature differences in winter.
6. Compute the thermal frequency ω_thermal and the power per unit area emitted by a surface with emissivity ϵ = 1 for
   1. T = 3 K (cosmic background temperature),
   2. T = 300 K (earth’s temperature),
   3. T = 6000 K (sun’s surface),
   4. and T = 2 × 10⁷ K (sun’s interior).
7. Derive an equation for the light pressure (force per unit area) acting on the walls of a box whose interior is at temperature T. Assume for simplicity that all photons being emitted and absorbed by a wall move in a direction normal to the wall. Compute this pressure for the interior of the sun. Hint: Recall that a photon with energy E has momentum E∕c, and that both emitted and absorbed photons transfer momentum to the wall.
8. Imagine two plates, each at temperature T as in figure 22.4, except that the left plate has emissivity ϵ_L and the right plate has emissivity ϵ_R, so that we cannot assume a priori that J_TOT is the same going to the left and to the right. Show that the radiative energy flux incident on each plate from the other is still σT⁴.
9. Two parallel plates facing each other, one at temperature \(T_{1}\), the other at temperature \(T_{2}\), each have emissivity ϵ = 1. Assuming that T₁ = 200 K and T₂ = 300 K, compute the net radiative transfer of energy per unit area per unit time from plate 2 to plate 1. 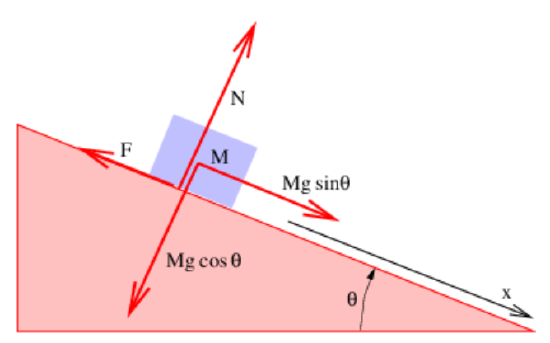Figure 22.7: Mass M subject to gravity, friction (F), and a normal force (N) on a ramp tilted at an angle θ with respect to the horizontal.
10. Imagine a mass sliding on a ramp subject to frictional and normal forces as shown in figure 22.7.
    1. If the coefficient of kinetic friction is μ_k, determine the acceleration down the ramp.
    2. Suppose the mass has been given a push so that it is sliding up the ramp. Determine its acceleration down the ramp.
    3. If the coefficient of static friction is μ_s, compute the maximum angle for which the mass in figure 22.7 will remain stationary.
11. Consider a layer of water at 20^∘ C between two plates, the bottom one stationary and the top one moving to the right, as shown in figure 22.6. The spacing between the plates is 1 mm and the top plate is moving at \(10 \mathrm{~m} \mathrm{~s}^{-1}\).
    1. Compute the drag force per unit area on the top plate.
    2. Compute the increase in temperature of the water after 100 s. Assume all work done by the plate is dissipated in the water. The density of water is \(1000 \mathrm{~kg} \mathrm{~m}^{-3}\)