1.9: Group Velocity

We now ask the following question: How fast do wave packets move? Surprisingly, we often find that wave packets move at a speed very different from the phase speed, \(c=\omega / k\) of the wave composing the wave packet.

We shall find that the speed of motion of wave packets, referred to as the group velocity, is given by

\[u=\left.\frac{d \omega}{d k}\right|_{k=k_{0}} \quad \text { (group velocity). }\label{1.36}\]

The derivative of \(\omega(k)\) with respect to \(k\) is first computed and then evaluated at \(k=k_{0}\) the central wavenumber of the wave packet of interest.

The relationship between the angular frequency and the wavenumber for a wave, \(\omega=\omega(k)\) depends on the type of wave being considered. Whatever this relationship turns out to be in a particular case, it is called the dispersion relation for the type of wave in question.

As an example of a group velocity calculation, suppose we want to find the velocity of deep ocean wave packets for a central wavelength of \(\lambda_{0}=60 \mathrm{~m}\). This corresponds to a central wavenumber of \(k_{0}=2 \pi \lambda_{0} \approx 0.1 \mathrm{~m}^{-1}\). The phase speed of deep ocean waves is \(c=(g / k)^{12}\). However, since \(c \equiv \omega / k,\) we find the frequency of deep ocean waves to be \(\omega=(g k)^{1 / 2}\). The group velocity is therefore \(u \equiv d \omega / d k=(g / k)^{12} / 2=c / 2\). For the specified central wavenumber, we find that \(u \approx\left(9.8 \mathrm{~m} \mathrm{~s}^{-2} / 0.1 \mathrm{~m}^{-1}\right)^{12} / 2 \approx 5 \mathrm{~m} \mathrm{~s}^{-1}\). By contrast, the phase speed of deep ocean waves with this wavelength is c ≈ 10 m s^-1.

Dispersive waves are waves in which the phase speed varies with wavenumber. It is easy to show that dispersive waves have unequal phase and group velocities, while these velocities are equal for non-dispersive waves.

Derivation of Group Velocity Formula

We now derive Equation \ref{1.36}. It is easiest to do this for the simplest wave packets, namely those constructed out of the superposition of just two sine waves. We will proceed by adding two waves with full space and time dependence:

\[h=\sin \left(k_{1} x-\omega_{1} t\right)+\sin \left(k_{2} x-\omega_{2} t\right)\label{1.37}\]

After algebraic and trigonometric manipulations familiar from earlier sections, we find

\[h=2 \sin \left(k_{0} x-\omega_{0} t\right) \cos (\Delta k x-\Delta \omega t)\label{1.38}\]

where as before we have \(k_{0}=\left(k_{1}+k_{2}\right) 2, \omega_{0}=\left(\omega_{1}+\omega_{2}\right) 2, \Delta k=\left(k_{2}-k_{1}\right) 2, \text { and } \Delta \omega=\left(\omega_{2}-\omega_{1}\right) 2\).

Figure \(\PageIndex{1}\): (left) Net displacement of the sum of two traveling sine waves plotted in the x - t plane. The white indicates where the displacement is large and positive, while the black indicates where it is large and negative. Non-dispersive case with u_p = u_g = 1.. (right) Plot of wave displacement as a function of \(x\) at time \(t = 0\).

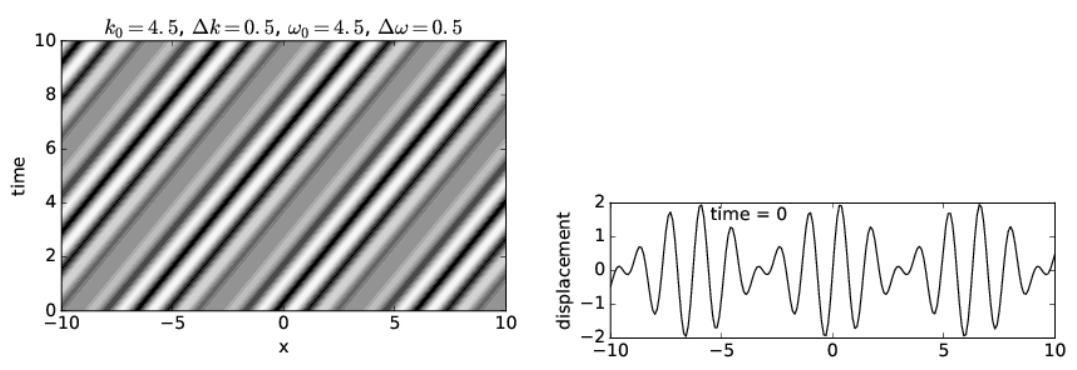
Again think of this as a sine wave of frequency ω₀ and wavenumber k₀ modulated by a cosine function. In this case the modulation pattern moves with a speed so as to keep the argument of the cosine function constant:

\[\Delta k x-\Delta \omega t=\text { const. }\label{1.39}\]

Differentiating this with respect to t while holding Δk and Δω constant yields

\[u \equiv \frac{d x}{d t}=\frac{\Delta \omega}{\Delta k}\label{1.40}\]

In the limit in which the deltas become very small, this reduces to the derivative

\[u=\frac{d \omega}{d k},\label{1.41}\]

which is the desired result.

Examples

We now illustrate some examples of phase speed and group velocity by showing the displacement resulting from the superposition of two sine waves, as given by Equation \ref{1.38}, in the x-t plane. This is an example of a space time diagram, of which we will see many examples later on.

Figure \(\PageIndex{2}\): (A; left) As in the upper panel of figure 1.16 except a dispersive case with u_p = 1, u_g = 2. (B; right) As in the upper panel of figure 1.16 except a dispersive case with phase and group velocities in opposite directions, u_p = 1, u_g = -1.

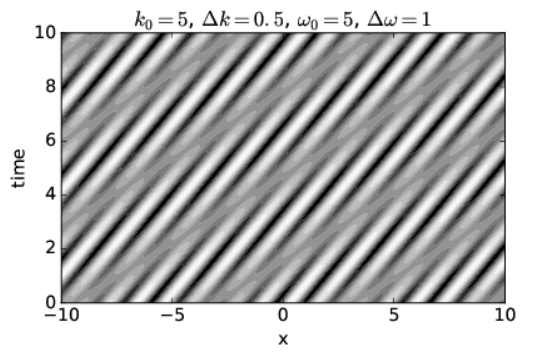
The upper panel of Figure \(\PageIndex{2A}\) shows a non-dispersive case in which the phase speed equals the group velocity. The white and black regions indicate respectively strong wave crests and troughs (i. e., regions of large positive and negative displacements), with grays indicating a displacement near zero. Regions with large displacements indicate the location of wave packets. The positions of waves and wave packets at any given time may therefore be determined by drawing a horizontal line across the graph at the desired time and examining the variations in wave displacement along this line. The lower panel of this figure shows the wave displacement as a function of \(x\) at time \(t = 0\) as an aid to interpretation of the upper panel.

Notice that as time increases, the crests move to the right. This corresponds to the motion of the waves within the wave packets. Note also that the wave packets, i. e., the broad regions of large positive and negative amplitudes, move to the right with increasing time as well.

Since velocity is distance moved Δx divided by elapsed time Δt, the slope of a line in Figure \(\PageIndex{2A}\), \(\Delta t / \Delta x\), is one over the velocity of whatever that line represents. The slopes of lines representing crests are the same as the slopes of lines representing wave packets in this case, which indicates that the two move at the same velocity. Since the speed of movement of wave crests is the phase speed and the speed of movement of wave packets is the group velocity, the two velocities are equal and the non-dispersive nature of this case is confirmed.

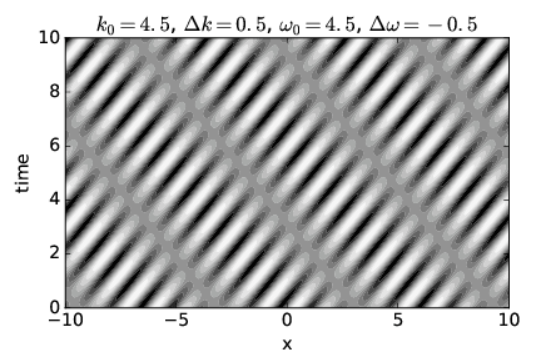
Figure \(\PageIndex{2A}\) shows a dispersive wave in which the group velocity is twice the phase speed, while Figure \(\PageIndex{2B}\) shows a case in which the group velocity is actually opposite in sign to the phase speed. See if you can confirm that the phase and group velocities seen in each figure correspond to the values for these quantities calculated from the specified frequencies and wavenumbers.