1.8: Math Review — Derivatives

Last updated
Save as PDF

Page ID: 33144

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

This section provides a quick review of the idea of the derivative. Often we are interested in the slope of a line tangent to a function y(x) at some value of x. This slope is called the derivative and is denoted dy∕dx. Since a tangent line to the function can be defined at any point x, the derivative itself is a function of x:

\[g(x)=\frac{d y(x)}{d x}\label{1.25}\]

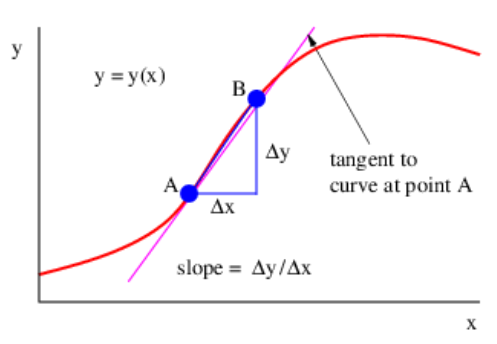
As figure 1.15 illustrates, the slope of the tangent line at some point on the function may be approximated by the slope of a line connecting two points, A and B, set a finite distance apart on the curve:

\[\frac{d y}{d x} \approx \frac{\Delta y}{\Delta x}\label{1.26}\]

As B is moved closer to A, the approximation becomes better. In the limit when B moves infinitely close to A, it is exact.

Figure \(\PageIndex{1}\): Estimation of the derivative, which is the slope of the tangent line. When point B approaches point A, the slope of the line AB approaches the slope of the tangent to the curve at point A.

Derivatives of some common functions are now given. In each case a is a constant.

\[\frac{d x^{a}}{d x}=a x^{a-1}\label{1.27}\]

\[\frac{d}{d x} \exp (a x)=a \exp (a x)\label{1.28}\]

\[\frac{d}{d x} \log (a x)=\frac{1}{x}\label{1.29}\]

\[\frac{d}{d x} \sin (a x)=a \cos (a x)\label{1.30}\]

\[\frac{d}{d x} \cos (a x)=-a \sin (a x)\label{1.31}\]

\[\frac{d a f(x)}{d x}=a \frac{d f(x)}{d x}\label{1.32}\]

\[\frac{d}{d x}[f(x)+g(x)]=\frac{d f(x)}{d x}+\frac{d g(x)}{d x}\label{1.33}\]

\[\frac{d}{d x} f(x) g(x)=\frac{d f(x)}{d x} g(x)+f(x) \frac{d g(x)}{d x} \quad \text { (product rule) }\label{1.34}\]

\[\frac{d}{d x} f(y)=\frac{d f}{d y} \frac{d y}{d x} \quad(\text { chain rule })\label{1.35}\]

The product and chain rules are used to compute the derivatives of complex functions. For instance,

\(\frac{d}{d x}(\sin (x) \cos (x))=\frac{d \sin (x)}{d x} \cos (x)+\sin (x) \frac{d \cos (x)}{d x}=\cos ^{2}(x)-\sin ^{2}(x)\)

and

\(\frac{d}{d x} \log (\sin (x))=\frac{1}{\sin (x)} \frac{d \sin (x)}{d x}=\frac{\cos (x)}{\sin (x)}\).