4.3: Postulates of Special Relativity
- Page ID
- 32942
As we learned previously, the principle of relativity states that the laws of physics are the same in all inertial reference frames. The principle of relativity applies to Einsteinian relativity just as it applies to Galilean relativity.
Notice that the constancy of the speed of light in all reference frames is consistent with the principle of relativity. However, as noted above, it is inconsistent with our notions as to how velocities add, or alternatively, how we think the world should look from reference frames moving at different speeds. We have called the classical way of understanding the view from different reference frames Galilean relativity. The new way that reconciles the behavior of objects moving at very high speeds is called Einsteinian relativity. Einstein’s great contribution was to discover the laws that tell us how the world looks from reference frames moving at high speeds relative to each other. These laws constitute a geometry of spacetime, and from them all of special relativity can be derived.
All of the observed facts about spacetime can be derived from two postulates:
- Whether two events are simultaneous depends on the reference frame from which they are viewed.
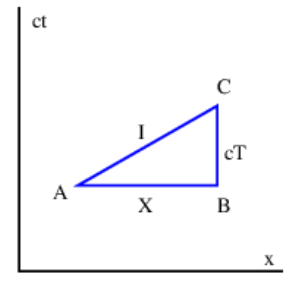
- Spacetime obeys a modified Pythagorean theorem, which gives the distance, I, in spacetime or spacetime interval as
\[I^{2}=X^{2}-c^{2} T^{2}\label{4.3}\]
where \(X\), \(T\), and \(I\) are defined in figure 4.4.
Let us discuss these postulates in turn.
Simultaneity
The classical way of thinking about simultaneity is so ingrained in our everyday habits that we have a great deal of difficulty adjusting to what special relativity has to say about this subject. Indeed, understanding how relativity changes this concept is the single most difficult part of the theory — once you understand this, you are well on your way to mastering relativity!
Before tackling simultaneity, let us first think about collocation. Two events (such as A and E in figure 4.5) are collocated if they have the same x value. However, collocation is a concept that depends on the reference frame. For instance, George is driving from Boston to Washington, with the line passing through events A and D being his world line. Just as he passes New York he sneezes (event A in figure 4.5). As he drives by Baltimore, he sneezes again (event D). In the reference frame of the earth, these two sneezes are not collocated, since they are separated by many kilometers. However, in the reference frame of George’s car, they occur in the same place — assuming that George hasn’t left the driver’s seat!
Notice that any two events separated by a timelike interval are collocated in some reference frame. The speed of the reference frame is given by equation (4.2.1), where the slope is simply the slope of the world line connecting the two events.
In Galilean relativity, if two events are simultaneous, we consider them to be simultaneous in all reference frames. For instance, if two clocks, one in New York and one in Los Angeles, strike the hour at the same time in the earth reference frame, then in Galilean relativity these events also appear to be simultaneous to instruments in the space shuttle as it flies over the United States. However, if the space shuttle is moving from west to east, i. e., from Los Angeles toward New York, careful measurements will show that the clock in New York strikes the hour before the clock in Los Angeles! Thus, the Galilean point of view is not accurate.
Just as collocation depends on one’s reference frame, this result shows that simultaneity also depends on the reference frame. Figure 4.5 shows how this works. In figure 4.5 events A and B are simultaneous in the rest or unprimed reference frame. However, in the primed reference frame, events A and C are simultaneous, and event B occurs at an earlier time. If A and B correspond to the clocks striking in Los Angeles and New York respectively, then it is clear that B must occur at an earlier time in the primed frame if indeed A and C are simultaneous in that frame.
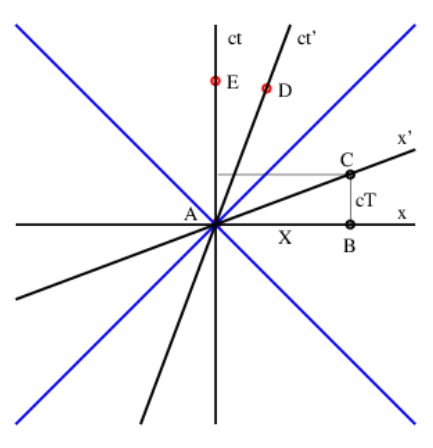
The tilted line passing through events A and C in figure 4.5 is called the line of simultaneity for the primed reference frame. Its slope is related to the speed, U, of the reference frame by
\[\text { slope }=U / c \quad \text { (line of simultaneity). }\label{4.4}\]
Notice that this is the inverse of the slope of the world line attached to the primed reference frame. There is thus a symmetry between the world line and the line of simultaneity of a moving reference frame — as the reference frame moves faster to the right, these two lines close like the blades of a pair of scissors on the 45∘ line.
In Galilean relativity it is fairly obvious what we mean by two events being simultaneous — it all boils down to coordinating portable clocks which are sitting next to each other, and then moving them to the desired locations. Two events separated in space are simultaneous if they occur at the same time on clocks located near each event, assuming that the clocks have been coordinated in the above manner.
In Einsteinian relativity this doesn’t work, because the very act of moving the clocks changes the rate at which the clocks run. Thus, it is more difficult to determine whether two distant events are simultaneous.
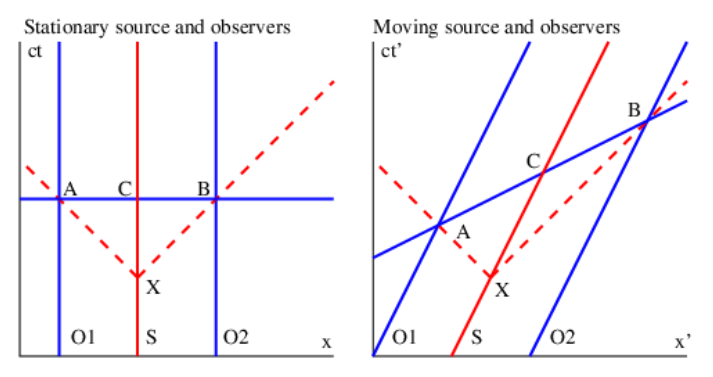
An alternate way of experimentally determining simultaneity is shown in figure 4.6. Since we know from observation that light travels at the same speed in all reference frames, the pulses of light emitted by the light sources in figure 4.6 will reach the two equidistant observers simultaneously in both cases. The line passing through these two events, A and B, defines a line of simultaneity for both stationary and moving observers. For the stationary observers this line is horizontal, as in Galilean relativity. For the moving observers the light has to travel farther in the rest frame to reach the observer receding from the light source, and it therefore takes longer in this frame. Thus, event B in the right panel of figure 4.6 occurs later than event A in the stationary reference frame and the line of simultaneity is tilted. We see that the postulate that light moves at the same speed in all reference frames leads inevitably to the dependence of simultaneity on reference frame.
Spacetime Pythagorean Theorem
The Pythagorean theorem of spacetime differs from the usual Pythagorean theorem in two ways. First, the vertical side of the triangle is multiplied by c. This is a trivial scale factor that gives time the same units as space. Second, the right side of equation (\ref{4.3}) has a minus sign rather than a plus sign. This highlights a fundamental difference between spacetime and the ordinary xyz space in which we live. Spacetime is said to have a non-Euclidean (but not curved) geometry — in other words, the normal rules of geometry that we learn in high school don’t always work for spacetime!
The main consequence of the minus sign in equation (\ref{4.3}) is that \(\mathrm{I}^{2}\) can be negative and therefore I can be imaginary. Furthermore, in the special case where \(\mathrm{X}=\pm \mathrm{cT}\), we actually have I = 0 even though X, \(\mathrm{T} \neq 0-\mathrm{i}\). e., the “distance” between two well-separated events can be zero. Clearly, spacetime has some weird properties!
The quantity I is usually called an interval in spacetime. Generally speaking, if \(\mathrm{I}^{2}\) is positive, the interval is called spacelike, while for a negative \(\mathrm{I}^{2}\), the interval is called timelike.
A concept related to the spacetime interval is the proper time τ. The proper time between the two events A and C in figure 4.4 is defined by the equation
\[\tau^{2}=T^{2}-X^{2} / c^{2}\label{4.5}\]
Notice that I and τ are related by
\[\tau^{2}=-I^{2} / c^{2}\label{4.6}\]
so the spacetime interval and the proper time are not independent concepts. However, I has the dimensions of length and is real when the events defining the interval are spacelike relative to each other, whereas τ has the dimensions of time and is real when the events are timelike relative to each other. Both equation (\ref{4.3}) and equation (\ref{4.5}) express the spacetime Pythagorean theorem.
If two events defining the end points of an interval have the same t value, then the interval is the ordinary space distance between the two events. On the other hand, if they have the same x value, then the proper time is just the time interval between the events. If the interval between two events is spacelike, but the events are not simultaneous in the initial reference frame, they can always be made simultaneous by choosing a reference frame in which the events lie on the same line of simultaneity. Thus, the meaning of the interval in that case is just the distance between the events in the new reference frame. Similarly, for events separated by a timelike interval, the proper time is just the time between two events in a reference frame in which the two events are collocated.