8.2: Potential Energy

We now address Newtonian mechanics in the case where the force on a particle is conservative. A conservative force is one that can be derived from a so-called potential energy U. We assume that the potential energy of the particle depends only on its position. The force is obtained from the potential energy by the equation

\[F=-\frac{d U}{d x}\label{8.2}\]

Using this equation we write Newton’s second law as

\[-\frac{d U}{d x}=m a\label{8.3}\]

We then notice that the acceleration can be written in terms of the x derivative along the particle’s trajectory of \(v^{2} / 2:\):

\[a=\frac{d v}{d t}=\frac{d v}{d x} \frac{d x}{d t}=\frac{d v}{d x} v=\frac{1}{2} \frac{d v^{2}}{d x}\label{8.4}\]

The last step in the above derivation can be verified by applying the product rule: \(\mathrm{dv}^{2} / \mathrm{dt}=\mathrm{d}(\mathrm{vv}) / \mathrm{dt}=\mathrm{v}(\mathrm{dv} / \mathrm{dt})+(\mathrm{dv} / \mathrm{dt}) \mathrm{v}=2 \mathrm{v}(\mathrm{dv} / \mathrm{dt})\). Putting equations (\ref{8.3}) and (\ref{8.4}) together, we find that \(\mathrm{d}\left(\mathrm{mv}^{2} / 2+\mathrm{U}\right) / \mathrm{dt}=0\), which implies that \(m v^{2} / 2+U\) is constant. We call this constant the total energy E and the quantity \(\mathrm{K}=\mathrm{mv}^{2} / 2\) the kinetic energy. We thus have the principle of conservation of energy for conservative forces:

\[E=K+U=\text { constant. }\label{8.5}\]

Figure 8.1: Example of spatially variable potential energy \(\mathrm{U}(\mathrm{x})\) for a particle with fixed total energy E. The kinetic energy \(\mathrm{K}=\mathrm{E}-\mathrm{U}\) is zero where the \(E\) and \(U\) lines cross. These points are called turning points. The thick part of the horizontal line indicates the allowed range for the particle with the given energy.

Recall that in quantum mechanics the momentum is related to the group velocity \(\mathrm{u}_{\mathrm{g}}\) by

\[\Pi=m u_{g} \quad \text { (momentum) }\label{8.6}\]

in the nonrelativistic case. Equating the group velocity to \(v\) and eliminating it in the kinetic energy results in an alternate expression for this quantity:

\[K \equiv \frac{1}{2} m u_{g}^{2}=\frac{\Pi^{2}}{2 m} \quad \text { (kinetic energy) }\label{8.7}\]

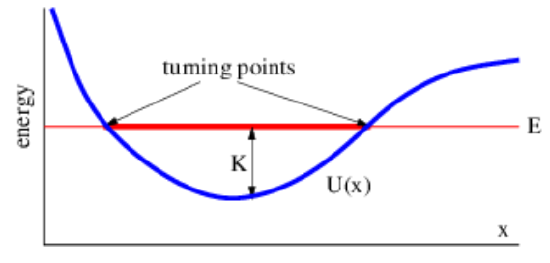
Since the total energy E is constant or conserved, increases in the potential energy coincide with decreases in the kinetic energy and vice versa, as is illustrated in figure 8.1. In classical mechanics the kinetic energy cannot be negative, since it is the product of half the mass and the square of the velocity, both of which are positive. Thus, a particle with total energy E and potential energy \(U\) is forbidden to venture into regions in which the kinetic energy \(\mathrm{K}=\mathrm{E}-\mathrm{U}\) is less than zero.

The points at which the kinetic energy is zero are called turning points. This is because a particle decreases in speed as it approaches a turning point, stops there for an instant, and reverses direction. Note also that a particle with a given total energy always has the same speed at some point x regardless of whether it approaches this point from the left or the right:

\[\text { speed }=\left|u_{g}\right|=\left|\pm[2(E-U) / m]^{1 / 2}\right|\label{8.8}\]

Gravity as a Conservative Force

An example of a conservative force is gravity. An object of mass m near the surface of the earth has the gravitational potential energy

\[U=m g z \quad \text { (gravity near earth's surface) }\label{8.9}\]

where \(z\) is the height of the object above some reference point such as the earth’s surface and \(g=9.8 \mathrm{~m} \mathrm{~s}^{-2}\) is the local value of the gravitational field near the surface. Notice that the gravitational potential energy increases upward. The speed of the object in this case is \(\left|u_{g}\right|=[2(E-m g z) / m]^{1 / 2}\). If \(\left|\mathrm{u}_{\mathrm{g}}\right|\) is known to equal the constant value \(\mathrm{u}_{0}\) at elevation z = 0, then equations (\ref{8.8}) and (\ref{8.9}) tell us that \(\mathrm{u}_{0}=(2 \mathrm{E} / \mathrm{m})^{1 / 2} \text { and }\left|\mathrm{u}_{\mathrm{g}}\right|=\left(\mathrm{u}_{0}^{2}-2 \mathrm{~g} \mathrm{z}\right)^{1 / 2}\).

There are certain types of questions which energy conservation cannot directly answer. For instance, if an object is released at elevation h with zero velocity at t = 0, at what time will it reach z = 0 under the influence of gravity? In such cases it is often easiest to return to Newton’s second law. Since the force on the object is F = -dU∕dz = -mg in this case, we find that the acceleration is \(a=F / m=-m g / m=-g\). However, \(a=d u / d t=d^{2} z / d t^{2}\), so

\[u=-g t+C_{1} \quad z=-g t^{2} / 2+C_{1} t+C_{2} \quad \text { (constant gravity) }\label{8.10}\]

where \(\mathrm{C}_{1} \text { and } \mathrm{C}_{2}\) are constants to be determined by the initial conditions. These results can be verified by differentiating to see if the original acceleration is recovered. Since \(\mathrm{u}=0 \text { and } z=\mathrm{h} \text { at } t=0\), we have \(\mathrm{C}_{1}=0 \text { and } \mathrm{C}_{2}=\mathrm{h}\). With these results it is easy to show that the object reaches \(z=0\) when \(\mathrm{t}=(2 \mathrm{~h} / \mathrm{g})^{1 / 2}\).