10.5: Rockets and Conveyor Belts

Normally when we define a system to which Newton’s second law is to be applied, the system is closed in the sense that mass cannot enter or exit the system. However, sometimes it is convenient to work with open systems for which this is not true. The classic example is the rocket, where exhaust gases leave the system, thus decreasing the mass of the rocket with time.

Open systems can be analyzed if momentum is considered to be a quantity which is accounted for much as money is accounted for in a bank account. The bank account can change in three ways: money can be deposited in the account, it can be withdrawn from the account, and the amount can grow or shrink as a consequence of interest payments or fees. Similarly, the amount of momentum in a system can change as the result of mass entering the system, mass leaving the system, and forces acting on the system. The time rate of change of momentum in a system is therefore

\[\frac{d p}{d t}=F+\left(\frac{d p}{d t}\right)_{i n}-\left(\frac{d p}{d t}\right)_{o u t}\label{10.16}\]

where F is the net force on the system, \((\mathrm{dp} / \mathrm{dt})_{\mathrm{in}}\) is the momentum per unit time added by mass entering the system, and \(\text { (dp /dt) }_{\text {out }}\) is the amount lost per unit time by mass exiting the system. In the non-relativistic case, \((\mathrm{dp} / \mathrm{dt})_{\mathrm{in}}=\mathrm{u}_{\mathrm{in}}(\mathrm{dm} / \mathrm{dt})_{\mathrm{in}} \text { and }(\mathrm{dp} / \mathrm{dt})_{\mathrm{out}}=\mathrm{u}_{\mathrm{out}}(\mathrm{dm} / \mathrm{dt})_{\mathrm{out}}\), where \((\mathrm{dm} / \mathrm{dt})_{\mathrm{in}}\) is the mass entering the system per unit time with velocity u_in and \((\mathrm{dm} / \mathrm{dt})_{\mathrm{out}}\) is the mass per unit time exiting the system with velocity \(\mathrm{u}_{\mathrm{out}}\).

For non-relativistic velocities, the momentum of the system can be written as \(p = mu\) so that

\[\frac{d p}{d t}=\frac{d m}{d t} u+m \frac{d u}{d t}\label{10.17}\]

To complete the analysis, we need an accounting of the mass entering and leaving the system:

\[\frac{d m}{d t}=\left(\frac{d m}{d t}\right)_{i n}-\left(\frac{d m}{d t}\right)_{o u t}\label{10.18}\]

Figure 10.5: Rocket moving with velocity V while expelling gas at a rate R with velocity V - u_x.

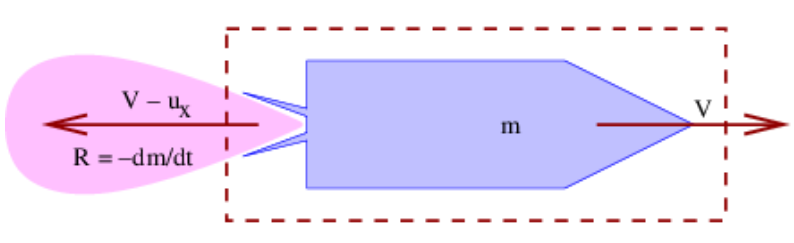
Let us see how to apply this to a rocket for which all velocities are non-relativistic. As figure 10.5 indicates, a rocket spews out a stream of exhaust gas. The system is defined by the dashed box and includes the rocket and the part of the exhaust gas inside the box. The reaction to the momentum carried off in this stream of gas is what causes the rocket to accelerate. We note that \((\mathrm{dm} / \mathrm{dt})_{\mathrm{in}}=0\) since no mass is entering the system, and \((\mathrm{dm} / \mathrm{dt})_{\mathrm{out}}=\mathrm{R}\), the rate at which mass is ejected by the rocket in the form of exhaust gas. The rocket is assumed to be moving to the right at speed V and the gas is ejected at a speed u_x relative to the rocket, which means that its actual velocity after ejection is V - u_x. We call u_x the exhaust velocity. Notice that V - u_x may be either positive or negative, depending on how big V is.

Equating the mass of the rocket to the system mass, we find that \(\mathrm{R}=-\mathrm{dm} / \mathrm{dt}\). The momentum balance equation (\ref{10.16}) becomes \(\mathrm{dp} / \mathrm{dt}=-\left(\mathrm{V}-\mathrm{u}_{\mathrm{x}}\right) \mathrm{R}\). The force on the rocket is actually zero, so the force term does not enter the momentum balance equation. This is non-intuitive, because we are used to acceleration being the result of a force. However, nothing, including the ejected gas, is actually pushing on the system, so we must indeed conclude that there is no force — all of the change in the system’s momentum arises from the ejection of gas with the opposite momentum.

Finally, we see that \(\mathrm{dp} / \mathrm{dt}=(\mathrm{dm} / \mathrm{dt}) \mathrm{V}+\mathrm{m}(\mathrm{dV} / \mathrm{dt})=-\mathrm{RV}+\mathrm{m}(\mathrm{dV} / \mathrm{dt})\). Equating this to the results of the momentum balance calculation gives us \(-\mathrm{RV}+\mathrm{m}(\mathrm{d} \mathrm{V} / \mathrm{dt})=-\left(\mathrm{V}-\mathrm{u}_{\mathrm{X}}\right) \mathrm{R}\). Solving for the acceleration \(\mathrm{dV} / \mathrm{dt}\) results in

\[\frac{d V}{d t}=\frac{u_{x} R}{m} \quad \text { (rocket acceleration) }\label{10.19}\]

Thus, the acceleration of the rocket depends on the exhaust velocity of the ejected gas, the rate at which the gas is being ejected, and the mass of the rocket.

Figure 10.6: Sand is dumped on a conveyor belt and in turn is dumped off the end of the belt.

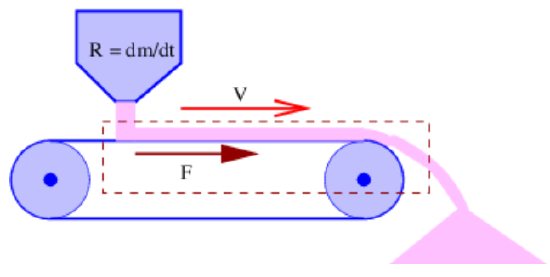
Figure 10.6 illustrates another type of open system problem. A hopper dumps sand on a conveyor belt at a rate of R kilograms per second. The conveyor belt is moving to the right at (non-relativistic) speed V and the sand is dumped off at the end. What force F is needed to keep the conveyor belt moving at a constant speed, assuming that the conveyor belt mechanism itself is frictionless? In this case \((\mathrm{dm} / \mathrm{dt})_{\mathrm{in}}=(\mathrm{dm} / \mathrm{dt})_{\text {out }}=\mathrm{R}\). Furthermore, since the system outlined by the dashed line is in a steady state, \(\mathrm{dp} / \mathrm{dt}=0\).

The key to understanding this problem is that the sand enters the system with zero horizontal velocity, but exits the system with the horizontal velocity of the conveyor belt, V . The momentum balance equation is thus

\[0=F-V R\label{10.20}\]

and the force is

\[F=V R \text { (force on conveyor belt). }\label{10.21}\]

This force serves to accelerate the sand up to the velocity of the conveyor belt.