10.4: Collisions

Let us now consider the situation in which two particles collide with each other. There can be several outcomes to this collision, of which we will study two:

• The two particles collide elastically, in essence bouncing off of each other.
• The two particles stick together, resulting in the production of a single particle, or a single particle breaks apart into two particles. These are inelastic processes.

In both of the above cases energy and momentum are conserved. We assume that the forces acting between the particles are short range, so that except in the instant of collision, we need not worry about potential energy or potential momentum — all energy is in the form of rest plus kinetic energy except in this short interval, and all momenta are kinetic momenta.

Because of the principle of relativity, we are free to consider collisions in any convenient reference frame. We can then transform the results to any reference frame we please. Generally speaking, the most convenient reference frame to consider is the one in which the total momentum of the two particles is zero. For the sake of simplicity we only consider collisions in one dimension.

Elastic Collisions

Figure 10.2: One-dimensional elastic collisions of two particles in the center of momentum frame as seen in spacetime diagrams.

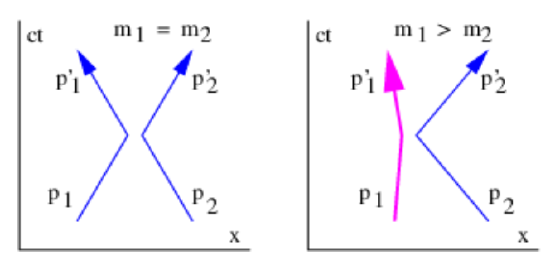
Suppose a particle with mass m₁ and initial velocity u₁ in the center of momentum frame, i. e., the reference frame in which the total momentum is zero, collides elastically with another particle of mass m₂ with initial velocity u₂. The momenta of the two particles are

\[p_{1}=\frac{m_{1} u_{1}}{\left(1-u_{1}^{2} / c^{2}\right)^{1 / 2}} \quad p_{2}=\frac{m_{2} u_{2}}{\left(1-u_{2}^{2} / c^{2}\right)^{1 / 2}}\label{10.7}\]

In the center of momentum frame we must have

\[p_{1}=-p_{2}\label{10.8}\]

Figure 10.2 shows what happens when these two particles collide. The first particle acquires momentum p₁′ while the second acquires momentum p₂′. The conservation of momentum tells us that the total momentum after the collision is the same as before the collision, namely zero, so

\[p_{1}^{\prime}=-p_{2}^{\prime}\label{10.9}\]

In the center of momentum frame we know that \(\left|p_{1}\right|=\left|p_{2}\right|\) and we know that the two momentum vectors point in opposite directions. Similarly, \(\left|p_{1}^{\prime}\right|=\left|p_{2}^{\prime}\right|\). However, we as yet don’t know how \(p_{1}^{\prime}\) is related to p₁. Conservation of energy,

\[E_{1}+E_{2}=E_{1}^{\prime}+E_{2}^{\prime}\label{10.10}\]

gives us this information. Notice that if \(\mathrm{p}_{1}{ }^{\prime}=-\mathrm{p}_{1} \text { , then } \mathrm{E}_{1}{ }^{\prime 2}=\mathrm{p}_{1}{ }^{\prime 2} \mathrm{c}^{2}+\mathrm{m}_{1}{ }^{2} \mathrm{c}^{4}=\mathrm{p}_{1}{ }^{2} \mathrm{c}^{2}+\mathrm{m}_{1}^{2} \mathrm{c}^{4}=\mathrm{E}_{1}^{2}\). Assuming positive energies, we therefore have \(\mathrm{E}_{1}{ }^{\prime}=\mathrm{E}_{1} . \text { If } \mathrm{p}_{2}{ }^{\prime}=-\mathrm{p}_{2}\), then we can similiarly infer that \(\mathrm{E}_{2}{ }^{\prime}=\mathrm{E}_{2}\). If these conditions are satisfied, then so is equation (\ref{10.10}). Therefore, a complete solution to the problem is

\[p_{1}=-p_{1}^{\prime}=-p_{2}=p_{2}^{\prime} \equiv p\label{10.11}\]

and

\[E_{1}=E_{1}^{\prime}=\left(p^{2} c^{2}+m_{1}^{2} c^{4}\right)^{1 / 2} \quad E_{2}=E_{2}^{\prime}=\left(p^{2} c^{2}+m_{2}^{2} c^{4}\right)^{1 / 2}\label{10.12}\]

In other words, the particles just exchange momenta.

The left panel of figure 10.2 shows what happens in a collision when the masses of the two colliding particles are equal. If \(m_{1}=m_{2}\), then the incoming and outgoing velocities of the two particles are the same, as indicated by the inverse slopes of the world lines. On the other hand, if \(m_{1}>m_{2}\), then the velocity of particle 2 is greater than the velocity of particle 1, as is illustrated in the right panel of figure 10.2.

Figure 10.3: Elastic collisions viewed from a reference frame in which one particle is initially stationary.

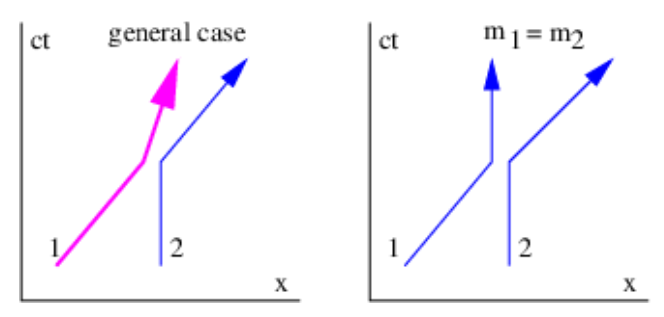
Suppose we wish to view the results of an elastic collision in a reference frame in which particle 2 is initially stationary. All we have to do is to transform the velocities into a reference frame moving with the initial velocity of particle 2, as illustrated in figure 10.3. We do this by relativistically adding \(U=-u_{2}\) to each velocity. (Note that the velocity U of the moving frame is positive since \(\mathrm{u}_{2}\) is negative.) Using the relativistic velocity translation formula, we find that

\[v_{1}=\frac{u_{1}+U}{1+u_{1} U / c^{2}} \quad v_{1}^{\prime}=\frac{u_{1}^{\prime}+U}{1+u_{1}^{\prime} U / c^{2}} \quad v_{2}^{\prime}=\frac{u_{2}^{\prime}+U}{1+u_{2}^{\prime} U / c^{2}}\label{10.13}\]

where \(\mathrm{u}_{1}, \mathrm{u}_{1}^{\prime}, \mathrm{u}_{2}, \text { and } \mathrm{u}_{2}{ }^{\prime}\) indicate velocities in the original, center of momentum reference frame and v₁, v₁′, etc., indicate velocities in the transformed frame.

In the special case where the masses of the two particles are equal to each other, we have \(\mathrm{v}_{1}=2 \mathrm{U} /\left(1+\mathrm{U}^{2} / \mathrm{c}^{2}\right), \mathrm{v}_{1}{ }^{\prime}=0, \text { and } \mathrm{v}_{2}{ }^{\prime}=2 \mathrm{U} /\left(1+\mathrm{U}^{2} / \mathrm{c}^{2}\right)=\mathrm{v}_{1}\). Thus, when the masses are equal, the particles simply exchange velocities.

If the velocities are nonrelativistic, then the simpler Galilean transformation law \(v=u+U\) can be used in place of the relativistic equations invoked above.

Inelastic Collisions

Figure 10.4: Building blocks of inelastic collisions. In the left panel two particles collide to form a third particle. In the right panel a particle breaks up, forming two particles.

An inelastic collision is one in which the particles coming out of the collision are not the same as the particles going into it. Inelastic collisions conserve both total momentum and energy just as elastic collisions do. However, unlike elastic collisions, inelastic collisions generally do not conserve the total kinetic energy of the particles, as some rest energy is generally created or destroyed.

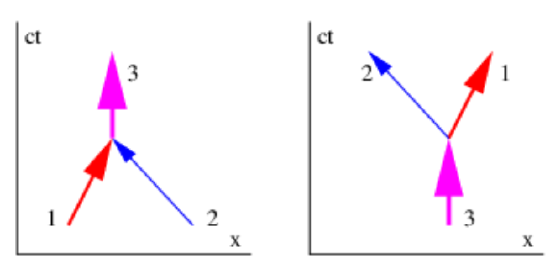
Figure 10.4 shows the fundamental building blocks of inelastic collisions. We can consider even the most complex inelastic collisions to be made up of composites of only two processes, the creation of one particle from two, and the disintegration of one particle into two.

Let us consider each of these in the center of momentum frame. In both cases the single particle must be stationary in this frame since it carries the total momentum of the system, which has to be zero. By conservation of momentum, if particle 1 in the left panel of figure 10.4 has momentum p, then the momentum of particle 2 is -p. If the two particles have masses m₁ and m₂, then their energies are \(E_{1}=\left(p^{2} c^{2}+m_{1}^{2} c^{4}\right)^{1 / 2} \text { and } E_{2}=\left(p^{2} c^{2}+m_{2}^{2} c^{4}\right)^{1 / 2}\). The energy of particle 3 is therefore \(\mathrm{E}_{3}=\mathrm{E}_{1}+\mathrm{E}_{2}\), and since it is at rest, all of its energy is in the form of “\(\mathrm{mc}^{2}\)” or rest energy, and so the mass of this particle is

\[\begin{equation}
\begin{aligned}
m_{3} &=\left(E_{1}+E_{2}\right) / c^{2} \quad(\text { center of momentum frame }) \\
&=\left(p^{2} / c^{2}+m_{1}^{2}\right)^{1 / 2}+\left(p^{2} / c^{2}+m_{2}^{2}\right)^{1 / 2} \\
&=m_{1}\left[1+p^{2} /\left(m_{1}^{2} c^{2}\right)\right]^{1 / 2}+m_{2}\left[1+p^{2} /\left(m_{2}^{2} c^{2}\right)\right]^{1 / 2}
\end{aligned}
\end{equation}\label{10.14}\]

The last line in the above equation shows that \(m_{3}>m_{1}+m_{2}\) because it is in the form \(m_{1} A+m_{2} B\) where both A and B are greater than one. Thus, rest energy is created in the amount \(\Delta \mathrm{E}_{\text {rest }}=\left(m_{3}-m_{1}-m_{2}\right) c^{2}\).

Actually, it is easy to calculate the mass of particle 3 in the above case from any reference frame as long as the momenta and energies of particles 1 and 2 are known in this frame. By conservation of energy and momentum, \(\mathrm{E}_{3}=\mathrm{E}_{1}+\mathrm{E}_{2} \text { and } \mathbf{p}_{3}=\mathbf{p}_{1}+\mathbf{p}_{2}\). Furthermore, \(\mathrm{E}_{3}^{2}=\mathrm{p}_{3}^{2} \mathrm{c}^{2}+\mathrm{m}_{3}^{2} \mathrm{c}^{4}\), so we can solve for m₃:

\[m_{3}=\left[\left(E_{1}+E_{2}\right)^{2} / c^{4}-\left(\mathbf{p}_{1}+\mathbf{p}_{2}\right) \cdot\left(\mathbf{p}_{1}+\mathbf{p}_{2}\right) / c^{2}\right]^{1 / 2} \quad(\text { any frame })\label{10.15}\]

The right panel of figure 10.4 shows the process of particle decay. This is just the inverse of the particle creation process, and all of the analysis we have done for creation is valid for particle decay except that rest energy is converted to kinetic energy rather than vice versa.