2.2: Images Formed by Plane Mirrors
- Page ID
- 4492
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Describe how an image is formed by a plane mirror.
- Distinguish between real and virtual images.
- Find the location and characterize the orientation of an image created by a plane mirror.
You only have to look as far as the nearest bathroom to find an example of an image formed by a mirror. Images in a plane mirror are the same size as the object, are located behind the mirror, and are oriented in the same direction as the object (i.e., “upright”).
To understand how this happens, consider Figure \(\PageIndex{1}\). Two rays emerge from point \(P\), strike the mirror, and reflect into the observer’s eye. Note that we use the law of reflection to construct the reflected rays. If the reflected rays are extended backward behind the mirror (see dashed lines), they seem to originate from point \(Q\). This is where the image of point \(P\) is located. If we repeat this process for point \(P′P′\), we obtain its image at point \(Q′\). You should convince yourself by using basic geometry that the image height (the distance from \(Q\) to \(Q′\)) is the same as the object height (the distance from \(P\) to \(P′\)). By forming images of all points of the object, we obtain an upright image of the object behind the mirror.
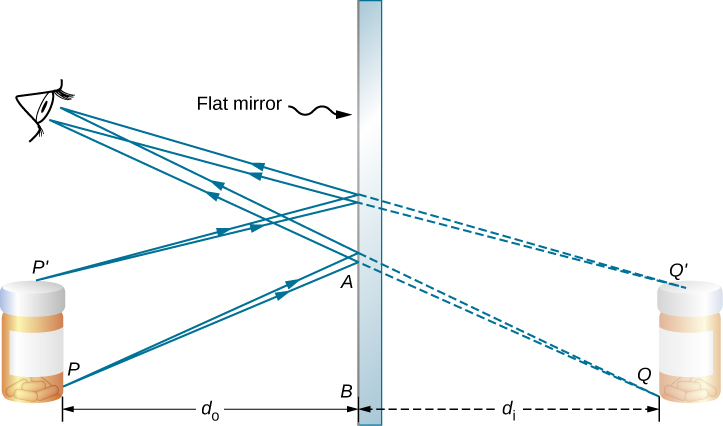
Notice that the reflected rays appear to the observer to come directly from the image behind the mirror. In reality, these rays come from the points on the mirror where they are reflected. The image behind the mirror is called a virtual image because it cannot be projected onto a screen—the rays only appear to originate from a common point behind the mirror. If you walk behind the mirror, you cannot see the image, because the rays do not go there. However, in front of the mirror, the rays behave exactly as if they come from behind the mirror, so that is where the virtual image is located.
Later in this chapter, we discuss real images; a real image can be projected onto a screen because the rays physically go through the image. You can certainly see both real and virtual images. The difference is that a virtual image cannot be projected onto a screen, whereas a real image can.
Locating an Image in a Plane Mirror
The law of reflection tells us that the angle of incidence is the same as the angle of reflection. Applying this to triangles \(PAB\) and \(QAB\) in Figure \(\PageIndex{1}\) and using basic geometry shows that they are congruent triangles. This means that the distance \(PB\) from the object to the mirror is the same as the distance \(BQ\) from the mirror to the image. The object distance (denoted \(d_o\)) is the distance from the mirror to the object (or, more generally, from the center of the optical element that creates its image). Similarly, the image distance (denoted \(d_i\)) is the distance from the mirror to the image (or, more generally, from the center of the optical element that creates it). If we measure distances from the mirror, then the object and image are in opposite directions, so for a plane mirror, the object and image distances should have the opposite signs:
An extended object such as the container in Figure \(\PageIndex{1}\) can be treated as a collection of points, and we can apply the method above to locate the image of each point on the extended object, thus forming the extended image.
Multiple Images
If an object is situated in front of two mirrors, you may see images in both mirrors. In addition, the image in the first mirror may act as an object for the second mirror, so the second mirror may form an image of the image. If the mirrors are placed parallel to each other and the object is placed at a point other than the midpoint between them, then this process of image-of-an-image continues without end, as you may have noticed when standing in a hallway with mirrors on each side. This is shown in Figure \(\PageIndex{2}\), which shows three images produced by the blue object. Notice that each reflection reverses front and back, just like pulling a right-hand glove inside out produces a left-hand glove (this is why a reflection of your right hand is a left hand). Thus, the fronts and backs of images 1 and 2 are both inverted with respect to the object, and the front and back of image 3 is inverted with respect to image 2, which is the object for image 3.
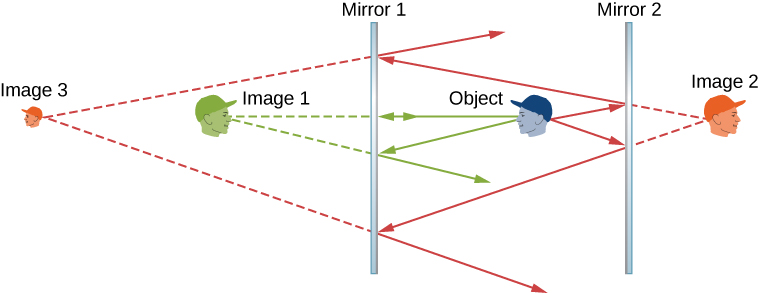
You may have noticed that image 3 is smaller than the object, whereas images 1 and 2 are the same size as the object. The ratio of the image height with respect to the object height is called magnification. More will be said about magnification in the next section.
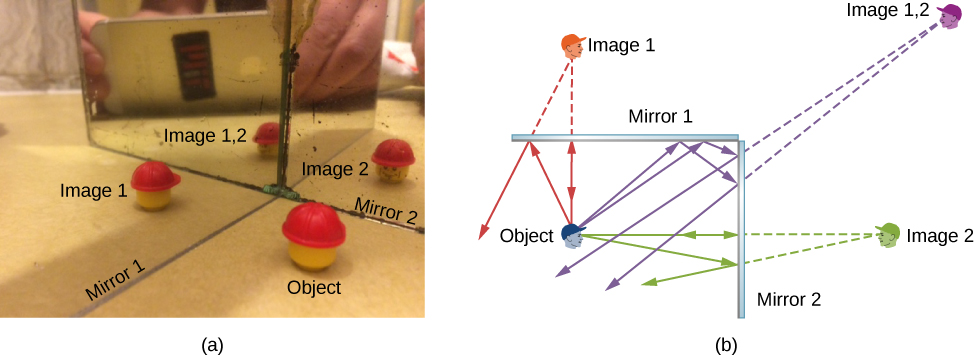
Infinite reflections may terminate. For instance, two mirrors at right angles form three images, as shown in Figure \(\PageIndex{3a}\). Images 1 and 2 result from rays that reflect from only a single mirror, but image 1,2 is formed by rays that reflect from both mirrors. This is shown in the ray-tracing diagram in (\PageIndex{3b}\). To find image 1,2, you have to look behind the corner of the two mirrors.