3.2: Young's Double-Slit Interference
- Page ID
- 4499
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Explain the phenomenon of interference
- Define constructive and destructive interference for a double slit
The Dutch physicist Christiaan Huygens (1629–1695) thought that light was a wave, but Isaac Newton did not. Newton thought that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous reputation, his view generally prevailed; the fact that Huygens’s principle worked was not considered direct evidence proving that light is a wave. The acceptance of the wave character of light came many years later in 1801, when the English physicist and physician Thomas Young (1773–1829) demonstrated optical interference with his now-classic double-slit experiment.
If there were not one but two sources of waves, the waves could be made to interfere, as in the case of waves on water (Figure \(\PageIndex{1}\)). If light is an electromagnetic wave, it must therefore exhibit interference effects under appropriate circumstances. In Young’s experiment, sunlight was passed through a pinhole on a board. The emerging beam fell on two pinholes on a second board. The light emanating from the two pinholes then fell on a screen where a pattern of bright and dark spots was observed. This pattern, called fringes, can only be explained through interference, a wave phenomenon.

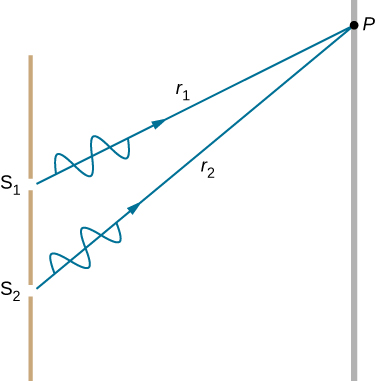
We can analyze double-slit interference with the help of Figure \(\PageIndex{2}\), which depicts an apparatus analogous to Young’s. Light from a monochromatic source falls on a slit \(S_0\). The light emanating from \(S_0\) is incident on two other slits \(S_1\) and \(S_2\) that are equidistant from \(S_0\). A pattern of interference fringes on the screen is then produced by the light emanating from \(S_1\) and \(S_2\). All slits are assumed to be so narrow that they can be considered secondary point sources for Huygens’ wavelets (The Nature of Light). Slits \(S_1\) and \(S_2\) are a distance d apart (\(d≤1\,mm\)), and the distance between the screen and the slits is D(≈1m), which is much greater than d.
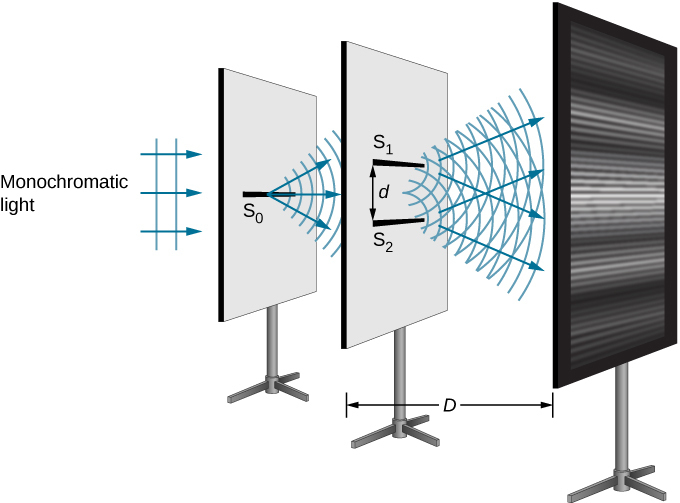
Since \(S_0\) is assumed to be a point source of monochromatic light, the secondary Huygens wavelets leaving \(S_1\) and \(S_2\) always maintain a constant phase difference (zero in this case because \(S_1\) and \(S_2\) are equidistant from \(S_0\)) and have the same frequency. The sources \(S_1\) and \(S_2\) are then said to be coherent. By coherent waves, we mean the waves are in phase or have a definite phase relationship. The term incoherent means the waves have random phase relationships, which would be the case if \(S_1\) and \(S_2\) were illuminated by two independent light sources, rather than a single source \(S_0\). Two independent light sources (which may be two separate areas within the same lamp or the Sun) would generally not emit their light in unison, that is, not coherently. Also, because \(S_1\) and \(S_2\) are the same distance from \(S_0\), the amplitudes of the two Huygens wavelets are equal.
Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. In the following discussion, we illustrate the double-slit experiment with monochromatic light (single λ) to clarify the effect. Figure \(\PageIndex{3}\) shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.
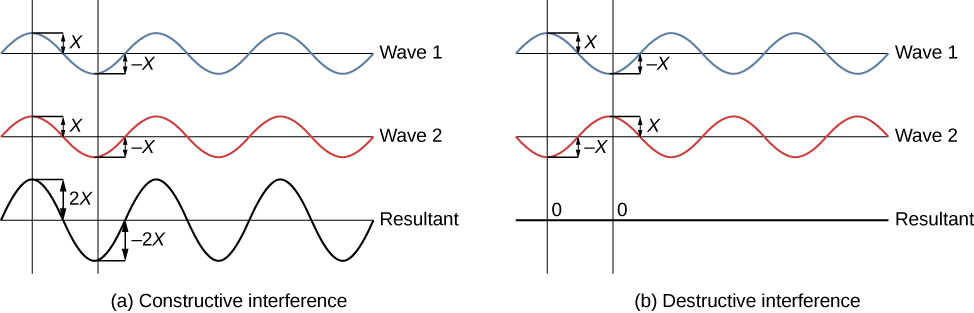
When light passes through narrow slits, the slits act as sources of coherent waves and light spreads out as semicircular waves, as shown in Figure \(\PageIndex{1a}\). Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure \(\PageIndex{1}\). Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.
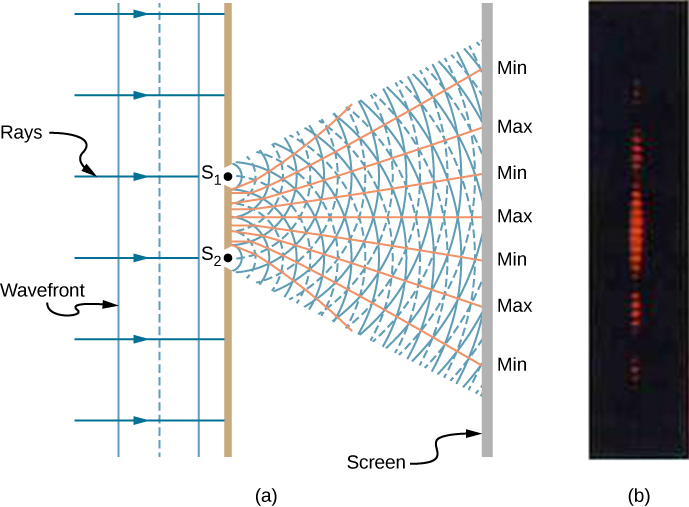
To understand the double-slit interference pattern, consider how two waves travel from the slits to the screen (Figure \(\PageIndex{5}\)). Each slit is a different distance from a given point on the screen. Thus, different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively. If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively. More generally, if the path length difference \(\Delta l\) between the two waves is any half-integral number of wavelengths [(1 / 2)λ, (3 / 2)λ, (5 / 2)λ, etc.], then destructive interference occurs. Similarly, if the path length difference is any integral number of wavelengths (λ, 2λ, 3λ, etc.), then constructive interference occurs. These conditions can be expressed as equations:
\[\underbrace{\Delta l = m \lambda}_{\text{constructive interference}} \nonumber \]
for \(m = 0, \, ±1, \, ±2, \, ±3…\)
\[\underbrace{\Delta l = \left(m + \frac{1}{2}\right)\lambda }_{\text{destructuve interference}} \nonumber \]
for \(m = 0, \, ±1, \, ±2, \, ±3…\)