4.E: Diffraction (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
4.1 Single-Slit Diffraction
1. As the width of the slit producing a single-slit diffraction pattern is reduced, how will the diffraction pattern produced change?
2. Compare interference and diffraction.
3. If you and a friend are on opposite sides of a hill, you can communicate with walkie-talkies but not with flashlights. Explain.
4. What happens to the diffraction pattern of a single slit when the entire optical apparatus is immersed in water?
5. In our study of diffraction by a single slit, we assume that the length of the slit is much larger than the width. What happens to the diffraction pattern if these two dimensions were comparable?
6. A rectangular slit is twice as wide as it is high. Is the central diffraction peak wider in the vertical direction or in the horizontal direction?
4.2 Intensity in Single-Slit Diffraction
7. In Equation 4.4, the parameter ββ looks like an angle but is not an angle that you can measure with a protractor in the physical world. Explain what ββ represents.
4.3 Double-Slit Diffraction
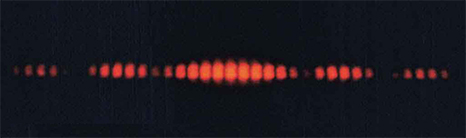
8. Shown below is the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single- and double-slit interference. Note that the bright spots are evenly spaced. Is this a double- or single-slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single- or double-slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses. Figure is an image showing red interference pattern on a black background. The central part has brighter lines. The lines are cut off at the top and bottom, seemingly enclosed between two sinusoidal waves of opposite phase.
4.5 Circular Apertures and Resolution
9. Is higher resolution obtained in a microscope with red or blue light? Explain your answer.
10. The resolving power of refracting telescope increases with the size of its objective lens. What other advantage is gained with a larger lens?
11. The distance between atoms in a molecule is about 10−8cm. Can visible light be used to “see” molecules?
12. A beam of light always spreads out. Why can a beam not be created with parallel rays to prevent spreading? Why can lenses, mirrors, or apertures not be used to correct the spreading?
4.6 X-Ray Diffraction
13. Crystal lattices can be examined with X-rays but not UV. Why?
4.7 Holography
14. How can you tell that a hologram is a true three-dimensional image and that those in three-dimensional movies are not?
15. If a hologram is recorded using monochromatic light at one wavelength but its image is viewed at another wavelength, say 10 shorter, what will you see? What if it is viewed using light of exactly half the original wavelength?
16. What image will one see if a hologram is recorded using monochromatic light but its image is viewed in white light? Explain.
Problems
4.1 Single-Slit Diffraction
17. (a) At what angle is the first minimum for 550-nm light falling on a single slit of width 1.00μm?
(b) Will there be a second minimum?
18. (a) Calculate the angle at which a 2.00−μm-wide slit produces its first minimum for 410-nm violet light.
(b) Where is the first minimum for 700-nm red light?
19. (a) How wide is a single slit that produces its first minimum for 633-nm light at an angle of \displaystyle 28.0°?
(b) At what angle will the second minimum be?
20. (a) What is the width of a single slit that produces its first minimum at \displaystyle 60.0° for 600-nm light?
(b) Find the wavelength of light that has its first minimum at \displaystyle 62.0°.
21. Find the wavelength of light that has its third minimum at an angle of \displaystyle 48.6° when it falls on a single slit of width \displaystyle 3.00μm.
22. (a) Sodium vapor light averaging 589 nm in wavelength falls on a single slit of width \displaystyle 7.50μm. At what angle does it produces its second minimum?
(b) What is the highest-order minimum produced?
23. Consider a single-slit diffraction pattern for \displaystyle λ=589nm, projected on a screen that is 1.00 m from a slit of width 0.25 mm. How far from the center of the pattern are the centers of the first and second dark fringes?
24. (a) Find the angle between the first minima for the two sodium vapor lines, which have wavelengths of 589.1 and 589.6 nm, when they fall upon a single slit of width \displaystyle 2.00μm.
(b) What is the distance between these minima if the diffraction pattern falls on a screen 1.00 m from the slit?
(c) Discuss the ease or difficulty of measuring such a distance.
25. (a) What is the minimum width of a single slit (in multiples of \displaystyle λ) that will produce a first minimum for a wavelength \displaystyle λ?
(b) What is its minimum width if it produces 50 minima?
(c) 1000 minima?
26. (a) If a single slit produces a first minimum at \displaystyle 14.5°, at what angle is the second-order minimum?
(b) What is the angle of the third-order minimum?
(c) Is there a fourth-order minimum?
(d) Use your answers to illustrate how the angular width of the central maximum is about twice the angular width of the next maximum (which is the angle between the first and second minima).
27. If the separation between the first and the second minima of a single-slit diffraction pattern is 6.0 mm, what is the distance between the screen and the slit? The light wavelength is 500 nm and the slit width is 0.16 mm.
28. A water break at the entrance to a harbor consists of a rock barrier with a 50.0-m-wide opening. Ocean waves of 20.0-m wavelength approach the opening straight on. At what angles to the incident direction are the boats inside the harbor most protected against wave action?
29. An aircraft maintenance technician walks past a tall hangar door that acts like a single slit for sound entering the hangar. Outside the door, on a line perpendicular to the opening in the door, a jet engine makes a 600-Hz sound. At what angle with the door will the technician observe the first minimum in sound intensity if the vertical opening is 0.800 m wide and the speed of sound is 340 m/s?
4.2 Intensity in Single-Slit Diffraction
30. A single slit of width \displaystyle 3.0μm is illuminated by a sodium yellow light of wavelength 589 nm. Find the intensity at a \displaystyle 15° angle to the axis in terms of the intensity of the central maximum.
31. A single slit of width 0.1 mm is illuminated by a mercury light of wavelength 576 nm. Find the intensity at a 10°10° angle to the axis in terms of the intensity of the central maximum.
32. The width of the central peak in a single-slit diffraction pattern is 5.0 mm. The wavelength of the light is 600 nm, and the screen is 2.0 m from the slit. (a) What is the width of the slit? (b) Determine the ratio of the intensity at 4.5 mm from the center of the pattern to the intensity at the center.
33. Consider the single-slit diffraction pattern for \displaystyle λ=600nm, a=0.025m, and \displaystyle x=2.0m. Find the intensity in terms of \displaystyle I_o at \displaystyle θ=0.5°, \displaystyle 1.0°, 1.5°, 3.0°, and \displaystyle 10.0°.
4.3 Double-Slit Diffraction
34. Two slits of width \displaystyle 2μm, each in an opaque material, are separated by a center-to-center distance of \displaystyle 6μm. A monochromatic light of wavelength 450 nm is incident on the double-slit. One finds a combined interference and diffraction pattern on the screen.
(a) How many peaks of the interference will be observed in the central maximum of the diffraction pattern?
(b) How many peaks of the interference will be observed if the slit width is doubled while keeping the distance between the slits same?
(c) How many peaks of interference will be observed if the slits are separated by twice the distance, that is, \displaystyle 12μm, while keeping the widths of the slits same?
(d) What will happen in (a) if instead of 450-nm light another light of wavelength 680 nm is used?
(e) What is the value of the ratio of the intensity of the central peak to the intensity of the next bright peak in (a)?
(f) Does this ratio depend on the wavelength of the light?
(g) Does this ratio depend on the width or separation of the slits?
35. A double slit produces a diffraction pattern that is a combination of single- and double-slit interference. Find the ratio of the width of the slits to the separation between them, if the first minimum of the single-slit pattern falls on the fifth maximum of the double-slit pattern. (This will greatly reduce the intensity of the fifth maximum.)
36. For a double-slit configuration where the slit separation is four times the slit width, how many interference fringes lie in the central peak of the diffraction pattern?
37. Light of wavelength 500 nm falls normally on 50 slits that are \displaystyle 2.5×10^{−3}mm wide and spaced \displaystyle 5.0×10^{−3}mm apart. How many interference fringes lie in the central peak of the diffraction pattern?
38. A monochromatic light of wavelength 589 nm incident on a double slit with slit width \displaystyle 2.5μm and unknown separation results in a diffraction pattern containing nine interference peaks inside the central maximum. Find the separation of the slits.
39. When a monochromatic light of wavelength 430 nm incident on a double slit of slit separation \displaystyle 5μm, there are 11 interference fringes in its central maximum. How many interference fringes will be in the central maximum of a light of the same wavelength and slit widths, but a new slit separation of \displaystyle 4 μm?
40. Determine the intensities of two interference peaks other than the central peak in the central maximum of the diffraction, if possible, when a light of wavelength 628 nm is incident on a double slit of width 500 nm and separation 1500 nm. Use the intensity of the central spot to be \displaystyle 1mW/cm^2.
4.4 Diffraction Gratings
41. A diffraction grating has 2000 lines per centimeter. At what angle will the first-order maximum be for 520-nm-wavelength green light?
42. Find the angle for the third-order maximum for 580-nm-wavelength yellow light falling on a difraction grating having 1500 lines per centimeter.
43. How many lines per centimeter are there on a diffraction grating that gives a first-order maximum for 470-nm blue light at an angle of \displaystyle 25.0° ?
44. What is the distance between lines on a diffraction grating that produces a second-order maximum for 760-nm red light at an angle of \displaystyle 60.0°?
45. Calculate the wavelength of light that has its second-order maximum at \displaystyle 45.0° when falling on a diffraction grating that has 5000 lines per centimeter.
46. An electric current through hydrogen gas produces several distinct wavelengths of visible light. What are the wavelengths of the hydrogen spectrum, if they form first-order maxima at angles \displaystyle 24.2°,25.7°,29.1°, and \displaystyle 41.0° when projected on a diffraction grating having 10,000 lines per centimeter?
47. (a) What do the four angles in the preceding problem become if a 5000-line per centimeter diffraction grating is used?
(b) Using this grating, what would the angles be for the second-order maxima?
(c) Discuss the relationship between integral reductions in lines per centimeter and the new angles of various order maxima.
48. What is the spacing between structures in a feather that acts as a reflection grating, giving that they produce a first-order maximum for 525-nm light at a \displaystyle 30.0° angle?
49. An opal such as that shown in Figure 4.15 acts like a reflection grating with rows separated by about \displaystyle 8μm. If the opal is illuminated normally,
(a) at what angle will red light be seen and
(b) at what angle will blue light be seen?
50. At what angle does a diffraction grating produce a second-order maximum for light having a first-order maximum at \displaystyle 20.0°?
51. (a) Find the maximum number of lines per centimeter a diffraction grating can have and produce a maximum for the smallest wavelength of visible light.
(b) Would such a grating be useful for ultraviolet spectra?
(c) For infrared spectra?
52. (a) Show that a 30,000 line per centimeter grating will not produce a maximum for visible light.
(b) What is the longest wavelength for which it does produce a first-order maximum?
(c) What is the greatest number of line per centimeter a diffraction grating can have and produce a complete second-order spectrum for visible light?
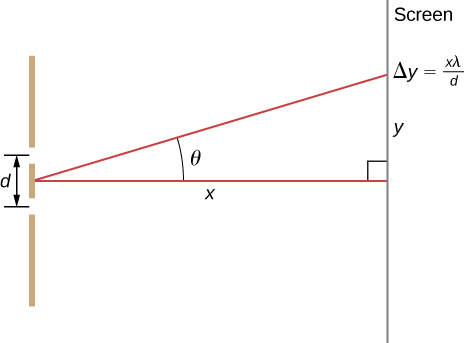
53. The analysis shown below also applies to diffraction gratings with lines separated by a distance d. What is the distance between fringes produced by a diffraction grating having 125 lines per centimeter for 600-nm light, if the screen is 1.50 m away? (Hint: The distance between adjacent fringes is \displaystyle Δy=xλ/d, assuming the slit separation d is comparable to \displaystyle λ.)
4.5 Circular Apertures and Resolution
54. The 305-m-diameter Arecibo radio telescope pictured in Figure 4.20 detects radio waves with a 4.00-cm average wavelength.
(a) What is the angle between two just-resolvable point sources for this telescope?
(b) How close together could these point sources be at the 2 million light-year distance of the Andromeda Galaxy?
55. Assuming the angular resolution found for the Hubble Telescope in Example 4.6, what is the smallest detail that could be observed on the moon?
56. Diffraction spreading for a flashlight is insignificant compared with other limitations in its optics, such as spherical aberrations in its mirror. To show this, calculate the minimum angular spreading of a flashlight beam that is originally 5.00 cm in diameter with an average wavelength of 600 nm.
57. (a) What is the minimum angular spread of a 633-nm wavelength He-Ne laser beam that is originally 1.00 mm in diameter? (b) If this laser is aimed at a mountain cliff 15.0 km away, how big will the illuminated spot be? (c) How big a spot would be illuminated on the moon, neglecting atmospheric effects? (This might be done to hit a corner reflector to measure the round-trip time and, hence, distance.)
58. A telescope can be used to enlarge the diameter of a laser beam and limit diffraction spreading. The laser beam is sent through the telescope in opposite the normal direction and can then be projected onto a satellite or the moon. (a) If this is done with the Mount Wilson telescope, producing a 2.54-m-diameter beam of 633-nm light, what is the minimum angular spread of the beam? (b) Neglecting atmospheric effects, what is the size of the spot this beam would make on the moon, assuming a lunar distance of \displaystyle 3.84×10^8m. ?
59. The limit to the eye’s acuity is actually related to diffraction by the pupil.
(a) What is the angle between two just-resolvable points of light for a 3.00-mm-diameter pupil, assuming an average wavelength of 550 nm?
(b) Take your result to be the practical limit for the eye. What is the greatest possible distance a car can be from you if you can resolve its two headlights, given they are 1.30 m apart?
(c) What is the distance between two just-resolvable points held at an arm’s length (0.800 m) from your eye?
(d) How does your answer to (c) compare to details you normally observe in everyday circumstances?
60. What is the minimum diameter mirror on a telescope that would allow you to see details as small as 5.00 km on the moon some 384,000 km away? Assume an average wavelength of 550 nm for the light received.
61. Find the radius of a star’s image on the retina of an eye if its pupil is open to 0.65 cm and the distance from the pupil to the retina is 2.8 cm. Assume \displaystyle λ=550nm.
62. (a) The dwarf planet Pluto and its moon, Charon, are separated by 19,600 km. Neglecting atmospheric effects, should the 5.08-m-diameter Palomar Mountain telescope be able to resolve these bodies when they are \displaystyle 4.50×10^9km from Earth? Assume an average wavelength of 550 nm.
(b) In actuality, it is just barely possible to discern that Pluto and Charon are separate bodies using a ground-based telescope. What are the reasons for this?
63. A spy satellite orbits Earth at a height of 180 km. What is the minimum diameter of the objective lens in a telescope that must be used to resolve columns of troops marching 2.0 m apart? Assume λ=550nm.λ=550nm.
64. What is the minimum angular separation of two stars that are just-resolvable by the 8.1-m Gemini South telescope, if atmospheric effects do not limit resolution? Use 550 nm for the wavelength of the light from the stars.
65. The headlights of a car are 1.3 m apart. What is the maximum distance at which the eye can resolve these two headlights? Take the pupil diameter to be 0.40 cm.
66. When dots are placed on a page from a laser printer, they must be close enough so that you do not see the individual dots of ink. To do this, the separation of the dots must be less than Raleigh’s criterion. Take the pupil of the eye to be 3.0 mm and the distance from the paper to the eye of 35 cm; find the minimum separation of two dots such that they cannot be resolved. How many dots per inch (dpi) does this correspond to?
67. Suppose you are looking down at a highway from a jetliner flying at an altitude of 6.0 km. How far apart must two cars be if you are able to distinguish them? Assume that \displaystyle λ=550nm and that the diameter of your pupils is 4.0 mm.
68. Can an astronaut orbiting Earth in a satellite at a distance of 180 km from the surface distinguish two skyscrapers that are 20 m apart? Assume that the pupils of the astronaut’s eyes have a diameter of 5.0 mm and that most of the light is centered around 500 nm.
69. The characters of a stadium scoreboard are formed with closely spaced lightbulbs that radiate primarily yellow light. (Use \displaystyle λ=600nm.) How closely must the bulbs be spaced so that an observer 80 m away sees a display of continuous lines rather than the individual bulbs? Assume that the pupil of the observer’s eye has a diameter of 5.0 mm.
70. If a microscope can accept light from objects at angles as large as \displaystyle α=70°, what is the smallest structure that can be resolved when illuminated with light of wavelength 500 nm and
(a) the specimen is in air?
(b) When the specimen is immersed in oil, with index of refraction of 1.52?
71. A camera uses a lens with aperture 2.0 cm. What is the angular resolution of a photograph taken at 700 nm wavelength? Can it resolve the millimeter markings of a ruler placed 35 m away?
4.6 X-Ray Diffraction
72. X-rays of wavelength 0.103 nm reflects off a crystal and a second-order maximum is recorded at a Bragg angle of \displaystyle 25.5°. What is the spacing between the scattering planes in this crystal?
73. A first-order Bragg reflection maximum is observed when a monochromatic X-ray falls on a crystal at a \displaystyle 32.3° angle to a reflecting plane. What is the wavelength of this X-ray?
74. An X-ray scattering experiment is performed on a crystal whose atoms form planes separated by 0.440 nm. Using an X-ray source of wavelength 0.548 nm, what is the angle (with respect to the planes in question) at which the experimenter needs to illuminate the crystal in order to observe a first-order maximum?
75. The structure of the NaCl crystal forms reflecting planes 0.541 nm apart. What is the smallest angle, measured from these planes, at which X-ray diffraction can be observed, if X-rays of wavelength 0.085 nm are used?
76. On a certain crystal, a first-order X-ray diffraction maximum is observed at an angle of \displaystyle 27.1° relative to its surface, using an X-ray source of unknown wavelength. Additionally, when illuminated with a different, this time of known wavelength 0.137 nm, a second-order maximum is detected at \displaystyle 37.3°. Determine (a) the spacing between the reflecting planes, and (b) the unknown wavelength.
77. Calcite crystals contain scattering planes separated by 0.30 nm. What is the angular separation between first and second-order diffraction maxima when X-rays of 0.130 nm wavelength are used?
78. The first-order Bragg angle for a certain crystal is \displaystyle 12.1°. What is the second-order angle?
Additional Problems
79. White light falls on two narrow slits separated by 0.40 mm. The interference pattern is observed on a screen 3.0 m away. (a) What is the separation between the first maxima for red light (\displaystyle λ=700nm) and violet light (\displaystyle λ=400nm)? (b) At what point nearest the central maximum will a maximum for yellow light (\displaystyle λ=600nm) coincide with a maximum for violet light? Identify the order for each maximum.
80. Microwaves of wavelength 10.0 mm fall normally on a metal plate that contains a slit 25 mm wide.
(a) Where are the first minima of the diffraction pattern?
(b) Would there be minima if the wavelength were 30.0 mm?
81. Quasars, or quasi-stellar radio sources, are astronomical objects discovered in 1960. They are distant but strong emitters of radio waves with angular size so small, they were originally unresolved, the same as stars. The quasar 3C405 is actually two discrete radio sources that subtend an angle of 82 arcsec. If this object is studied using radio emissions at a frequency of 410 MHz, what is the minimum diameter of a radio telescope that can resolve the two sources?
82. Two slits each of width 1800 nm and separated by the center-to-center distance of 1200 nm are illuminated by plane waves from a krypton ion laser-emitting at wavelength 461.9 nm. Find the number of interference peaks in the central diffraction peak.
83. A microwave of an unknown wavelength is incident on a single slit of width 6 cm. The angular width of the central peak is found to be \displaystyle 25°. Find the wavelength.
84. Red light (wavelength 632.8 nm in air) from a Helium-Neon laser is incident on a single slit of width 0.05 mm. The entire apparatus is immersed in water of refractive index 1.333. Determine the angular width of the central peak.
85. A light ray of wavelength 461.9 nm emerges from a 2-mm circular aperture of a krypton ion laser. Due to diffraction, the beam expands as it moves out. How large is the central bright spot at
(a) 1 m,
(b) 1 km,
(c) 1000 km, and
(d) at the surface of the moon at a distance of 400,000 km from Earth.
86. How far apart must two objects be on the moon to be distinguishable by eye if only the diffraction effects of the eye’s pupil limit the resolution? Assume 550 nm for the wavelength of light, the pupil diameter 5.0 mm, and 400,000 km for the distance to the moon.
87. How far apart must two objects be on the moon to be resolvable by the 8.1-m-diameter Gemini North telescope at Mauna Kea, Hawaii, if only the diffraction effects of the telescope aperture limit the resolution? Assume 550 nm for the wavelength of light and 400,000 km for the distance to the moon.
88. A spy satellite is reputed to be able to resolve objects 10. cm apart while operating 197 km above the surface of Earth. What is the diameter of the aperture of the telescope if the resolution is only limited by the diffraction effects? Use 550 nm for light.
89. Monochromatic light of wavelength 530 nm passes through a horizontal single slit of width \displaystyle 1.5μm in an opaque plate. A screen of dimensions \displaystyle 2.0m×2.0m is 1.2 m away from the slit.
(a) Which way is the diffraction pattern spread out on the screen?
(b) What are the angles of the minima with respect to the center?
(c) What are the angles of the maxima?
(d) How wide is the central bright fringe on the screen?
(e) How wide is the next bright fringe on the screen?
90. A monochromatic light of unknown wavelength is incident on a slit of width \displaystyle 20μm. A diffraction pattern is seen at a screen 2.5 m away where the central maximum is spread over a distance of 10.0 cm. Find the wavelength.
91. A source of light having two wavelengths 550 nm and 600 nm of equal intensity is incident on a slit of width \displaystyle 1.8μm. Find the separation of the \displaystyle m=1 bright spots of the two wavelengths on a screen 30.0 cm away.
92. A single slit of width 2100 nm is illuminated normally by a wave of wavelength 632.8 nm. Find the phase difference between waves from the top and one third from the bottom of the slit to a point on a screen at a horizontal distance of 2.0 m and vertical distance of 10.0 cm from the center.
93. A single slit of width \displaystyle 3.0μm is illuminated by a sodium yellow light of wavelength 589 nm. Find the intensity at a \displaystyle 15° angle to the axis in terms of the intensity of the central maximum.
94. A single slit of width 0.10 mm is illuminated by a mercury lamp of wavelength 576 nm. Find the intensity at a \displaystyle 10° angle to the axis in terms of the intensity of the central maximum.
95. A diffraction grating produces a second maximum that is 89.7 cm from the central maximum on a screen 2.0 m away. If the grating has 600 lines per centimeter, what is the wavelength of the light that produces the diffraction pattern?
96. A grating with 4000 lines per centimeter is used to diffract light that contains all wavelengths between 400 and 650 nm. How wide is the first-order spectrum on a screen 3.0 m from the grating?
97. A diffraction grating with 2000 lines per centimeter is used to measure the wavelengths emitted by a hydrogen gas discharge tube. (a) At what angles will you find the maxima of the two first-order blue lines of wavelengths 410 and 434 nm? (b) The maxima of two other first-order lines are found at \displaystyle θ_1=0.097rad and \displaystyle θ_2=0.132rad. What are the wavelengths of these lines?
98. For white light (\displaystyle 400nm<λ<700nm) falling normally on a diffraction grating, show that the second and third-order spectra overlap no matter what the grating constant d is.
99. How many complete orders of the visible spectrum (\displaystyle 400nm<λ<700nm) can be produced with a diffraction grating that contains 5000 lines per centimeter?
100. Two lamps producing light of wavelength 589 nm are fixed 1.0 m apart on a wooden plank. What is the maximum distance an observer can be and still resolve the lamps as two separate sources of light, if the resolution is affected solely by the diffraction of light entering the eye? Assume light enters the eye through a pupil of diameter 4.5 mm.
101. On a bright clear day, you are at the top of a mountain and looking at a city 12 km away. There are two tall towers 20.0 m apart in the city. Can your eye resolve the two towers if the diameter of the pupil is 4.0 mm? If not, what should be the minimum magnification power of the telescope needed to resolve the two towers? In your calculations use 550 nm for the wavelength of the light.
102. Radio telescopes are telescopes used for the detection of radio emission from space. Because radio waves have much longer wavelengths than visible light, the diameter of a radio telescope must be very large to provide good resolution. For example, the radio telescope in Penticton, BC in Canada, has a diameter of 26 m and can be operated at frequencies as high as 6.6 GHz.
(a) What is the wavelength corresponding to this frequency?
(b) What is the angular separation of two radio sources that can be resolved by this telescope?
(c) Compare the telescope’s resolution with the angular size of the moon.

103. Calculate the wavelength of light that produces its first minimum at an angle of \displaystyle 36.9° when falling on a single slit of width \displaystyle 1.00μm.
104. (a) Find the angle of the third diffraction minimum for 633-nm light falling on a slit of width \displaystyle 20.0μm.
(b) What slit width would place this minimum at \displaystyle 85.0°?
105. As an example of diffraction by apertures of everyday dimensions, consider a doorway of width 1.0 m.
(a) What is the angular position of the first minimum in the diffraction pattern of 600-nm light?
(b) Repeat this calculation for a musical note of frequency 440 Hz (A above middle C). Take the speed of sound to be 343 m/s.
106. What are the angular positions of the first and second minima in a diffraction pattern produced by a slit of width 0.20 mm that is illuminated by 400 nm light? What is the angular width of the central peak?
107. How far would you place a screen from the slit of the previous problem so that the second minimum is a distance of 2.5 mm from the center of the diffraction pattern?
108. How narrow is a slit that produces a diffraction pattern on a screen 1.8 m away whose central peak is 1.0 m wide? Assume \displaystyle λ=589nm.
109. Suppose that the central peak of a single-slit diffraction pattern is so wide that the first minima can be assumed to occur at angular positions of ±90°±90°. For this case, what is the ratio of the slit width to the wavelength of the light?
110. The central diffraction peak of the double-slit interference pattern contains exactly nine fringes. What is the ratio of the slit separation to the slit width?
111. Determine the intensities of three interference peaks other than the central peak in the central maximum of the diffraction, if possible, when a light of wavelength 500 nm is incident normally on a double slit of width 1000 nm and separation 1500 nm. Use the intensity of the central spot to be \displaystyle 1mW/cm^2.
112. The yellow light from a sodium vapor lamp seems to be of pure wavelength, but it produces two first-order maxima at \displaystyle 36.093° and \displaystyle 36.129° when projected on a 10,000 line per centimeter diffraction grating. What are the two wavelengths to an accuracy of 0.1 nm?
113. Structures on a bird feather act like a reflection grating having 8000 lines per centimeter. What is the angle of the first-order maximum for 600-nm light?
114. If a diffraction grating produces a first-order maximum for the shortest wavelength of visible light at \displaystyle 30.0°, at what angle will the first-order maximum be for the largest wavelength of visible light?
115. (a) What visible wavelength has its fourth-order maximum at an angle of \displaystyle 25.0° when projected on a 25,000-line per centimeter diffraction grating?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
116. Consider a spectrometer based on a diffraction grating. Construct a problem in which you calculate the distance between two wavelengths of electromagnetic radiation in your spectrometer. Among the things to be considered are the wavelengths you wish to be able to distinguish, the number of lines per meter on the diffraction grating, and the distance from the grating to the screen or detector. Discuss the practicality of the device in terms of being able to discern between wavelengths of interest.
117. An amateur astronomer wants to build a telescope with a diffraction limit that will allow him to see if there are people on the moons of Jupiter.
(a) What diameter mirror is needed to be able to see 1.00-m detail on a Jovian moon at a distance of \displaystyle 7.50×10^8km from Earth? The wavelength of light averages 600 nm.
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Challenge Problems
118. Blue light of wavelength 450 nm falls on a slit of width 0.25 mm. A converging lens of focal length 20 cm is placed behind the slit and focuses the diffraction pattern on a screen.
(a) How far is the screen from the lens?
(b) What is the distance between the first and the third minima of the diffraction pattern?
119. (a) Assume that the maxima are halfway between the minima of a single-slit diffraction pattern. The use the diameter and circumference of the phasor diagram, as described in Intensity in Single-Slit Diffraction, to determine the intensities of the third and fourth maxima in terms of the intensity of the central maximum.
(b) Do the same calculation, using Equation 4.4.
120. (a) By differentiating Equation 4.4, show that the higher-order maxima of the single-slit diffraction pattern occur at values of \displaystyle β that satisfy \displaystyle tanβ=β.
(b) Plot \displaystyle y=tanβ and \displaystyle y=β versus \displaystyle β and find the intersections of these two curves. What information do they give you about the locations of the maxima?
(c) Convince yourself that these points do not appear exactly at \displaystyle β=(n+\frac{1}{2})π, where \displaystyle n=0,1,2,…, but are quite close to these values.
121. What is the maximum number of lines per centimeter a diffraction grating can have and produce a complete first-order spectrum for visible light?
122. Show that a diffraction grating cannot produce a second-order maximum for a given wavelength of light unless the first-order maximum is at an angle less than \displaystyle 30.0°.
123. A He-Ne laser beam is reflected from the surface of a CD onto a wall. The brightest spot is the reflected beam at an angle equal to the angle of incidence. However, fringes are also observed. If the wall is 1.50 m from the CD, and the first fringe is 0.600 m from the central maximum, what is the spacing of grooves on the CD?
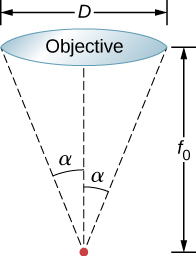
124. Objects viewed through a microscope are placed very close to the focal point of the objective lens. Show that the minimum separation x of two objects resolvable through the microscope is given by
x=\frac{1.22λf_0}{D}, \nonumber
where \displaystyle f_0 is the focal length and D is the diameter of the objective lens as shown below.