6.5: Conductors in Electrostatic Equilibrium
- Page ID
- 4382
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Describe the electric field within a conductor at equilibrium
- Describe the electric field immediately outside the surface of a charged conductor at equilibrium
- Explain why if the field is not as described in the first two objectives, the conductor is not at equilibrium
So far, we have generally been working with charges occupying a volume within an insulator. We now study what happens when free charges are placed on a conductor. Generally, in the presence of a (generally external) electric field, the free charge in a conductor redistributes and very quickly reaches electrostatic equilibrium. The resulting charge distribution and its electric field have many interesting properties, which we can investigate with the help of Gauss’s law and the concept of electric potential.
The Electric Field inside a Conductor Vanishes
If an electric field is present inside a conductor, it exerts forces on the free electrons (also called conduction electrons), which are electrons in the material that are not bound to an atom. These free electrons then accelerate. However, moving charges by definition means nonstatic conditions, contrary to our assumption. Therefore, when electrostatic equilibrium is reached, the charge is distributed in such a way that the electric field inside the conductor vanishes.
If you place a piece of a metal near a positive charge, the free electrons in the metal are attracted to the external positive charge and migrate freely toward that region. The region the electrons move to then has an excess of electrons over the protons in the atoms and the region from where the electrons have migrated has more protons than electrons. Consequently, the metal develops a negative region near the charge and a positive region at the far end (Figure \(\PageIndex{1}\)). As we saw in the preceding chapter, this separation of equal magnitude and opposite type of electric charge is called polarization. If you remove the external charge, the electrons migrate back and neutralize the positive region.
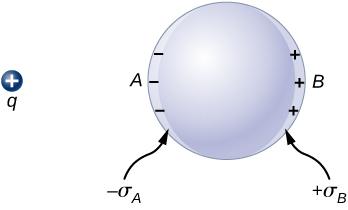
The polarization of the metal happens only in the presence of external charges. You can think of this in terms of electric fields. The external charge creates an external electric field. When the metal is placed in the region of this electric field, the electrons and protons of the metal experience electric forces due to this external electric field, but only the conduction electrons are free to move in the metal over macroscopic distances. The movement of the conduction electrons leads to the polarization, which creates an induced electric field in addition to the external electric field (Figure \(\PageIndex{2}\)). The net electric field is a vector sum of the fields of \(+q\) and the surface charge densities \(-\sigma_A\) and \(+\sigma_B\). This means that the net field inside the conductor is different from the field outside the conductor.
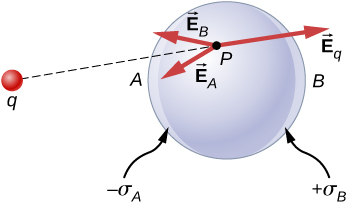
The redistribution of charges is such that the sum of the three contributions at any point \(P\) inside the conductor is
\[\vec{E}_p = \vec{E}_q + \vec{E}_B + \vec{E}_A = \vec{0}. \nonumber \]
Now, thanks to Gauss’s law, we know that there is no net charge enclosed by a Gaussian surface that is solely within the volume of the conductor at equilibrium. That is, \(q_{enc} = 0\) and hence
\[\vec{E}_{net} = \vec{0} \ \text{(at points inside a conductor)}. \nonumber \]
Charge on a Conductor
An interesting property of a conductor in static equilibrium is that extra charges on the conductor end up on the outer surface of the conductor, regardless of where they originate. Figure \(\PageIndex{3}\) illustrates a system in which we bring an external positive charge inside the cavity of a metal and then touch it to the inside surface. Initially, the inside surface of the cavity is negatively charged and the outside surface of the conductor is positively charged. When we touch the inside surface of the cavity, the induced charge is neutralized, leaving the outside surface and the whole metal charged with a net positive charge.
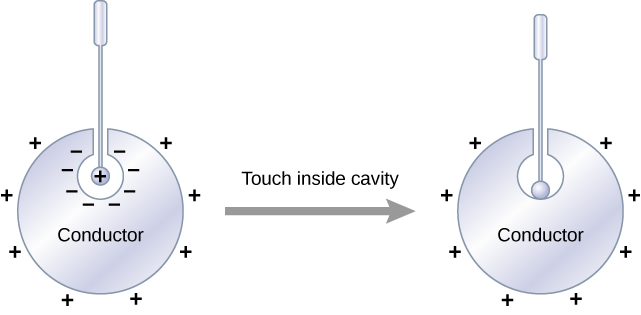
To see why this happens, note that the Gaussian surface in iFigure \(\PageIndex{4}\) (the dashed line) follows the contour of the actual surface of the conductor and is located an infinitesimal distance within it. Since \(E = 0\) everywhere inside a conductor,
\[\oint \vec{E} \cdot \hat{n} dA = 0. \nonumber \]
Thus, from Gauss’ law, there is no net charge inside the Gaussian surface. But the Gaussian surface lies just below the actual surface of the conductor; consequently, there is no net charge inside the conductor. Any excess charge must lie on its surface.
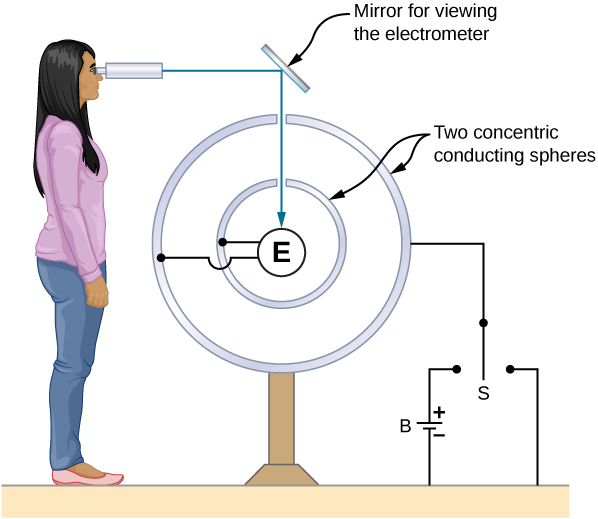
This particular property of conductors is the basis for an extremely accurate method developed by Plimpton and Lawton in 1936 to verify Gauss’s law and, correspondingly, Coulomb’s law. A sketch of their apparatus is shown in Figure \(\PageIndex{5}\). Two spherical shells are connected to one another through an electrometer E, a device that can detect a very slight amount of charge flowing from one shell to the other. When switch S is thrown to the left, charge is placed on the outer shell by the battery B. Will charge flow through the electrometer to the inner shell?
No. Doing so would mean a violation of Gauss’s law. Plimpton and Lawton did not detect any flow and, knowing the sensitivity of their electrometer, concluded that if the radial dependence in Coulomb’s law were \(1/r^{2+\delta}\), \(\delta\) would be less than \(2 \times 10^{-9}\) 1. More recent measurements place \(\delta\) at less than \(3 \times 10^{-16}\) 2, a number so small that the validity of Coulomb’s law seems indisputable.
\(^1\)S. Plimpton and W. Lawton. 1936. “A Very Accurate Test of Coulomb’s Law of Force between Charges.” Physical Review 50, No. 11:
1066, doi:10.1103/PhysRev.50.1066
\(^2\)E. Williams, J. Faller, and H. Hill. 1971. “New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest
Mass.” Physical Review Letters 26, No. 12: 721, doi:10.1103/PhysRevLett.26.721
The Electric Field at the Surface of a Conductor
If the electric field had a component parallel to the surface of a conductor, free charges on the surface would move, a situation contrary to the assumption of electrostatic equilibrium. Therefore, the electric field is always perpendicular to the surface of a conductor.
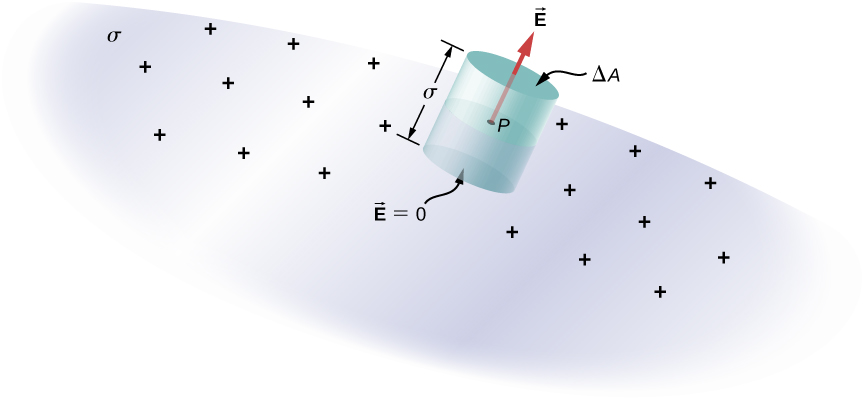
At any point just above the surface of a conductor, the surface charge density \(\delta\) and the magnitude of the electric field \(E\) are related by
\[E = \dfrac{\sigma}{\epsilon_0}. \nonumber \]
To see this, consider an infinitesimally small Gaussian cylinder that surrounds a point on the surface of the conductor, as in Figure \(\PageIndex{6}\). The cylinder has one end face inside and one end face outside the surface. The height and cross-sectional area of the cylinder are \(\delta\) and \(\Delta A\), respectively. The cylinder’s sides are perpendicular to the surface of the conductor, and its end faces are parallel to the surface. Because the cylinder is infinitesimally small, the charge density \(\sigma\) is essentially constant over the surface enclosed, so the total charge inside the Gaussian cylinder is \(\sigma\Delta A\). Now \(E\) is perpendicular to the surface of the conductor outside the conductor and vanishes within it, because otherwise, the charges would accelerate, and we would not be in equilibrium. Electric flux therefore crosses only the outer end face of the Gaussian surface and may be written as \(E\Delta A\) since the cylinder is assumed to be small enough that \(E\) is approximately constant over that area. From Gauss’ law,
\[E\Delta A = \dfrac{\sigma \Delta A}{\epsilon_0}. \nonumber \]
Thus
\[E = \dfrac{\sigma}{\epsilon_0}. \nonumber \]
The infinite conducting plate in Figure \(\PageIndex{7}\) has a uniform surface charge density \(\sigma\). Use Gauss’ law to find the electric field outside the plate. Compare this result with that previously calculated directly.
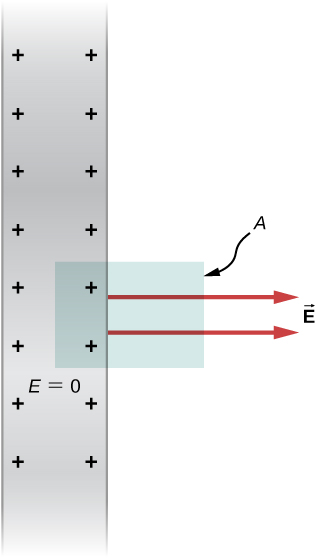
Strategy
For this case, we use a cylindrical Gaussian surface, a side view of which is shown.
Solution
The flux calculation is similar to that for an infinite sheet of charge from the previous chapter with one major exception: The left face of the Gaussian surface is inside the conductor where \(\vec{E} = \vec{0}\), so the total flux through the Gaussian surface is \(EA\) rather than \(2EA\). Then from Gauss’ law,
\[EA = \dfrac{\sigma A}{\epsilon_0} \nonumber \]
and the electric field outside the plate is
\[E = \dfrac{\sigma}{\epsilon_0}. \nonumber \]
Significance
This result is in agreement with the result from the previous section, and consistent with the rule stated above.
Two large conducting plates carry equal and opposite charges, with a surface charge density \(\sigma\) of magnitude \(6.81 \times 10^{-7} \mathrm{C}/\mathrm{m}^2\), as shown in Figure \(\PageIndex{8}\). The separation between the plates is \(l = 6.50 \, \mathrm{mm}\). What is the electric field between the plates?
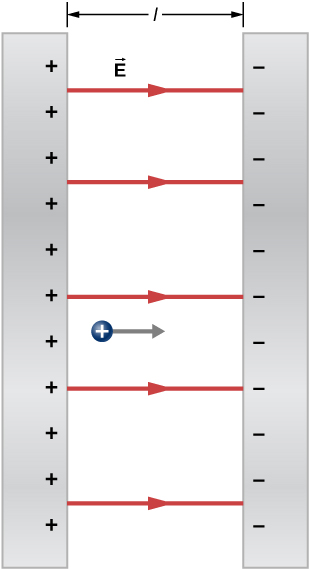
Strategy Note that the electric field at the surface of one plate only depends on the charge on that plate. Thus, apply \(E = \sigma /\epsilon_0\) with the given values.
Solution The electric field is directed from the positive to the negative plate, as shown in the figure, and its magnitude is given by
\[E = \dfrac{\sigma}{\epsilon_0} = \dfrac{6.81 \times 10^{-7} \mathrm{C}/\mathrm{m}^2}{8.85 \times 10^{-12} \mathrm{C}^2/\mathrm{N}\cdot\mathrm{m}^2} = 7.69 \times 10^4 \mathrm{N}/\mathrm{C} \nonumber \]
Significance
This formula is applicable to more than just a plate. Furthermore, two-plate systems will be important later.
The isolated conducting sphere (Figure \(\PageIndex{9}\)) has a radius \(R\) and an excess charge \(q\). What is the electric field both inside and outside the sphere?
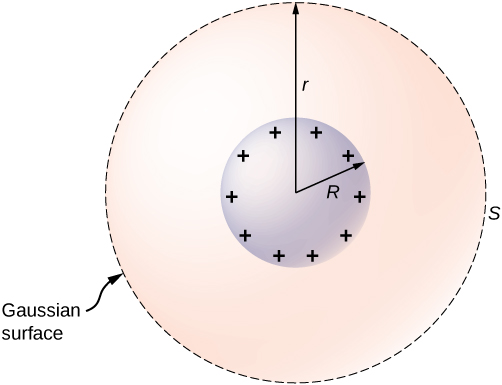
Strategy The sphere is isolated, so its surface change distribution and the electric field of that distribution are spherically symmetrical. We can therefore represent the field as \(\vec{E} = E(r) \hat{r}\). To calculate \(E(r)\), we apply Gauss’s law over a closed spherical surface \(S\) of radius \(r\) that is concentric with the conducting sphere.
Solution
Since \(r\) is constant and \(\hat{n} = \hat{r}\) on the sphere,
\[\oint_S \vec{E} \cdot \hat{n} dA = E(r) \oint_S dA = E(r) 4\pi r^2. \nonumber \]
For \(r < R\), \(S\) is within the conductor, so \(q_{enc} = 0\), and Gauss’s law gives
\[E(r) = 0, \nonumber \]
as expected inside a conductor. If \(r > R\), \(S\) encloses the conductor so \(q_{enc} = q\). From Gauss’s law,
\[E(r) 4\pi r^2 = \dfrac{q}{\epsilon_0}. \nonumber \]
The electric field of the sphere may therefore be written as
\[\vec{E} = \vec{0} \, (r < R), \nonumber \]
\[\vec{E} = \frac{1}{4\pi \epsilon_0} \frac{q}{r^2} \hat{r} \, (r \geq R). \nonumber \]
Significance
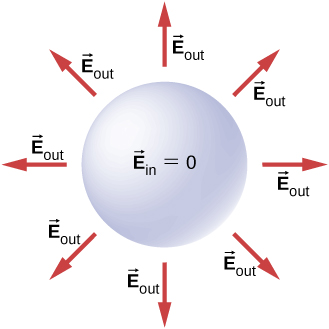
Notice that in the region \(r \geq R\), the electric field due to a charge \(q\) placed on an isolated conducting sphere of radius \(R\) is identical to the electric field of a point charge \(q\) located at the center of the sphere. The difference between the charged metal and a point charge occurs only at the space points inside the conductor. For a point charge placed at the center of the sphere, the electric field is not zero at points of space occupied by the sphere, but a conductor with the same amount of charge has a zero electric field at those points (Figure \(\PageIndex{10}\)). However, there is no distinction at the outside points in space where \(r > R\), and we can replace the isolated charged spherical conductor by a point charge at its center with impunity.
How will the system above change if there are charged objects external to the sphere?
- Answer
-
If there are other charged objects around, then the charges on the surface of the sphere will not necessarily be spherically symmetrical; there will be more in certain direction than in other directions.
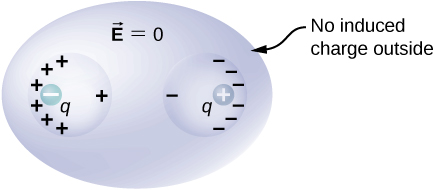
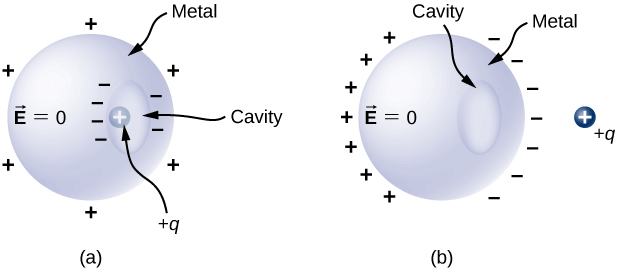
For a conductor with a cavity, if we put a charge \(+q\) inside the cavity, then the charge separation takes place in the conductor, with \(-q\) amount of charge on the inside surface and a \(+q\) amount of charge at the outside surface (Figure \(\PageIndex{11a}\)). For the same conductor with a charge \(+q\) outside it, there is no excess charge on the inside surface; both the positive and negative induced charges reside on the outside surface (Figure \(\PageIndex{11b}\)).
If a conductor has two cavities, one of them having a charge \(+q_a\) inside it and the other a charge \(-q_b\)the polarization of the conductor results in \(-q_a\)on the inside surface of the cavity \(a\), \(+q_b\) on the inside surface of the cavity \(b\), and \(q_a - q_b\) on the outside surface (Figure \(\PageIndex{12}\)). The charges on the surfaces may not be uniformly spread out; their spread depends upon the geometry. The only rule obeyed is that when the equilibrium has been reached, the charge distribution in a conductor is such that the electric field by the charge distribution in the conductor cancels the electric field of the external charges at all space points inside the body of the conductor.