1.5: Examples
( \newcommand{\kernel}{\mathrm{null}\,}\)
Example 1.5.1: Motion with (Piecewise) Constant Velocity
You leave your house on your bicycle to go visit a friend. At your normal speed of 9 mph, you know it takes you 6 minutes to get there. This time, though, when you have traveled half the distance you realize you forgot a book at home that you were going to return to your friend, so you turn around and pedal at twice your normal speed, get back home, grab the book, and start off again for your friend’s house at 18 mph (imagine you are really fit to pull this off!)
- How far away from you does your friend live?
- What is the total distance you travel on this trip?
- How long did the whole trip take?
- Draw a position versus time and a velocity versus time graph for the whole trip. Use SI units for both graphs. Neglect the time it takes you to stop and turn around, and also the time it takes you to run into your house and grab the book (in other words, assume those changes in your direction of motion happen instantly).
- Show explicitly, using your v-vs-t graph, that the graphical method of Figure 1.2.5 gives you the total displacement for your trip.
Solution
I am going to work out this problem using both miles and SI units, the first because it seems most natural, and the second because we are asked to use SI units for part (d), so we might as well use them from the start. In general, you should use SI units whenever you can. If you are unsure of what to do in a specific problem, ask your instructor!
(a) We are told that at 9 miles per hour it would take 6 minutes to get there, so let us use
Δx=vΔt
with v = 9 mph and Δt = 6 min. We have to either convert the hours to minutes, or vice-versa. Again, in this case it seems easiest to realize that 6 min equals 1/10 of an hour, so:
Δx=(9 miles hr )×0.1hr=0.9 miles.
In SI units, 9 mph = 4.023 m/s, and 6 min = 360 s, so Δx = 1448 m.
(b) This is just a matter of keeping track of the distance traveled in the various parts of the trip. You start by riding half the distance to your friend’s house, which is to say, 0.45 miles, and then you ride that again back home, so that’s 0.9 miles, and then you’re back where you started, so you still have to go the 0.9 miles to your friend’s house. So overall, you ride for 1.8 miles, or 2897 m.
(c) The whole trip consists, as detailed above, of 0.45 miles at 9 mph, and the rest, which is 1.35 miles, at 18 mph. Applying Δt=Δx/v to each of these intervals, we get a total time of
Δt=0.45 miles 9mph+1.35 miles 18mph=0.125 hours =0.125×60min=7.5min=7.5×60s=450s
(d) The graphs are shown below. Details on how to get them follow.

- First interval: from t = 0 to t = 180 s (3 min, which is what it would take to cover half the distance to your friend’s house at 9 mph). The velocity is a constant v = 4.023 m/s. For the position graph, use Equation (1.2.10) with xi = 0, ti = 0 and v = 4.023 m/s.
- Second interval: from t = 180 s to t = 270 s (it takes you half of 3 min, which is to say 90 s, to cover the same distance as above at twice the speed). The velocity is a constant v = −8.046 m/s (twice what it was earlier, but in the opposite direction). For the position graph, use Equation (1.2.10) with xi = 724 m (this is half of the distance to your friend’s house, and the starting position for this interval), ti = 180 s and v = −8.046 m/s.
- Third interval: from t = 270 s to t = 450 s. The velocity is a constant v = 8.046 m/s (same speed as just before, but in the opposite direction). For the position graph, use Equation (1.2.10) with xi = 0 m (you start back at your house), ti = 270 s and v = 8.046 m/s.
If you are familiar with the software package Mathematica, the position graph was produced using the command
Plot[If[t<180, 4.023 t, If[t<270, 4.023*180-8.046
(t-180), 8.046 (t-270)]], {t, 0, 450}]
and the velocity graph was produced using
Plot[If[t<180, 4.023 , If[t<270, -8.046, 8.046]],
{t, 0, 450}]
(and then connecting the horizontal lines by hand, which is not necessary, but helps to visualize what’s going on).
The graphs could also have been produced using the free plotting software package Gnuplot (available here: http://www.gnuplot.info/download.html) with the following commands:
gnuplot> set dummy t
gnuplot> f(t) = t<180 ? 4.023*t : t<270 ?
4.023*180-8.046*(t-180) : 8.046*(t-270)
gnuplot> plot [0:450] f(t)
The first line sets the default independent variable to t (instead of x, which is what Gnuplot expects). The second line defines the piecewise function using the ternary operator (? :) borrowed from the C programming language. The third line plots the function over the range indicated.
(e) For this we need to find the area under the v-vs-t graph we just plotted. Basically, we have three rectangles: the first one has base 180 units (s) and height 4 units (m/s), so its area is 4 × 180 = 720 (m). The second rectangle has base 90 units and height −8 (negative, because it is below the horizontal axis!), so its area is −720. The last one has base 180 units again (from 270 to 450) and height 8, so its area is 8 × 180 = 1440. So the total area “under” the v-vs-t curve is
720−72+1440=1440meters
which is (approximately) your total displacement, that is, the 9 miles to your friend’s house. (Of course, we would have obtained a more accurate result if we had used the more accurate values for the “heights” of 4.023, −8.046, and 8.046, but if all we have to go by is the graph, such accuracy is pretty much impossible.)
Example 1.5.2: Addition of velocities, relative motion
This example was inspired by the “race on a moving sidewalk” demo at http://physics.bu.edu/~duffy/classroom.html. Please go take a look at it!
Two girls, Ann and Becky (yes, A and B) decide to have a race while they wait for a plane at a nearly-deserted airport. Ann will run on the moving walkway, to the end of it (which is 30 m away) and back, whereas Becky will run alongside her on the (non-moving) floor, also 30 m out and back. The walkway moves at 1 m/s, and the girls both run at the same constant speed of 5 m/s relative to the surface they are standing on.
- Relative to the (non-moving) floor, what is Ann’s velocity for the first leg of her race, when she is moving in the same direction as the walkway (take that to be the positive direction)? What is her velocity for the return leg?
- How long does it take each of the girls to complete their race?
- When both girls are running in the positive direction, what is Becky’s velocity relative to Ann? (That is, how fast does Ann see Becky move, and in what direction?)
- When Ann turns around and starts running in the negative direction, but Becky is still running in the positive direction, what is Becky’s velocity relative to Ann?
- What is the total distance Ann runs in the moving walkway’s frame of reference?
Solution
I am going to solve this in the format that you will be required to use this semester for most of the homework and exam problems. I will not be able to do this for every single example, but you should! Please follow this carefully.
To begin with, you must draw a sketch of the situation described in the problem, detailed enough to include all the relevant information you are given. Here is mine:
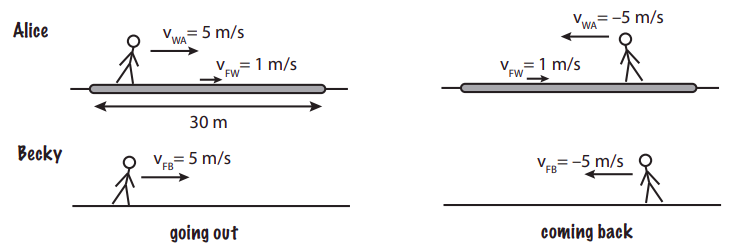
Note that I have drawn one picture for each half of the race, and that all the information given in the text of the problem is there. The figure makes it clear also the notation I will be using for each of the girls’ velocities, and to see at a glance what is happening.
You should next state what kind of problem this is and what basic result (theorem, principle, or equation(s)) you are going to use to solve it. For this problem, you could say:
“This is a relative motion/reference frame transformation problem. I will use Equation (1.3.6)
→vAP=→vBP+→vAB
as well as the basic equation for motion with constant velocity:”
Δx=vΔt.
After that, solve each part in turn, and make sure to show all your work!
(a) Let F stand for the floor frame of reference, and W the walkway frame. In the notation of Section 1.3, we have vFW = 1 m/s. For the first leg of her race, we are told that Ann’s velocity relative to the walkway is 5 m/s, so vWA = 5 m/s. Then, by Equation (1.3.6) (with the following change of indices: A → F, B → W, and P → A),
vFA=vFW+vWA=1ms+5ms=6ms
(when you see an equation like this, full of subscripts, it is a good practice to read it out, mentally, to yourself: “Ann’s velocity relative to the floor equals the velocity of the walkway relative to the floor plus Ann’s velocity relative to the walkway.” Then take a moment to see if it makes sense! Here is a place where the picture can be really helpful.)
For the return leg, use the same formula, but note that now her velocity relative to the walkway is negative, vWA = −5 m/s, since she is moving in the opposite direction:
vFA=vFW+vWA=1ms−5ms=−4ms.
(b) Relative to the floor reference frame, we have just seen that Ann first covers 30 m at a speed of 6 m/s, and then the same 30 m at a speed of 4 m/s, so her total time is
ΔtA=30m6m/s+30m4m/s=5s+7.5s=12.5s
whereas Becky just runs 30 m at 5 m/s both ways, so it takes her 6 s either way, for a total of 12 s, which means she wins the race.
(c) The quantity we want is written, in the notation of Section 1.3, vAB (“velocity of Becky relative to Ann”). To calculate this, we just need to know the velocities of both girls in some frame of reference (the same for both!), then subtract Ann’s velocity from Becky’s (this is what Equation (1.3.8) is saying). In this case, if we just choose the floor’s reference frame, we have vFA = 6 m/s and vFB = 5 m/s, so
vAB=vFB−vFA=5ms−6ms=−1ms
The negative sign makes sense: Ann sees Becky falling behind her, so relative to her Becky is moving backwards, which is to say, in the direction we have identified as negative.
(d) Again we use the same equation, and Becky’s velocity is still the same, but now Ann’s velocity is vFA = −4 m/s (note the negative sign!), so
vAB=vFB−vFA=5ms−(−4ms)=9ms
(e) You may find this a bit surprising, but if you think about it the explanation for why Ann lost the race, despite her running at the same speed as Becky relative to the surface she was standing on, has to be that she actually ran a longer distance on that surface! Since she was running for a total of 12.5 s at a constant speed (not velocity!) of 5 m/s in the walkway frame, then in that frame she ran a distance d=|v|Δt=5×12.5=62.5 m. That is the total length of walkway that she actually stepped on.


