1.6: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 1.6.1
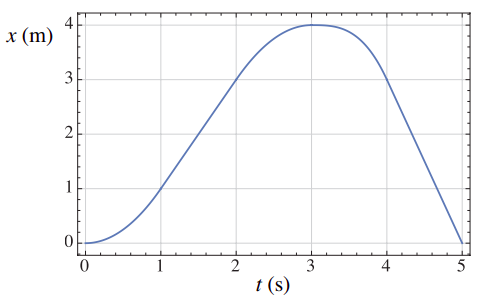
The above figure is the position (in meters) versus time (in seconds) graph of an object in motion. Only the segments between t = 1 s and t = 2 s, and between t = 4 s and t = 5 s, are straight lines. The peak of the curve is at t = 3 s, x = 4 m.
Answer the following questions, and provide a brief justification for your answer in every case.
- At what time(s) is the object’s velocity equal to zero?
- For what range(s) of times is the object moving with constant velocity?
- What is the object’s position coordinate at t = 1 s?
- What is the displacement of the object between t = 1 s and t = 4 s?
- What is the distance traveled between t = 1 s and t = 4 s?
- What is the instantaneous velocity of the object at t = 1.5 s?
- What is its average velocity between t = 1 s and t = 3 s?
Exercise 1.6.2
A particle is initially at xi = 3 m, yi = −5 m, and after a while it is found at the coordinates xf = −4 m, yf = 2 m.
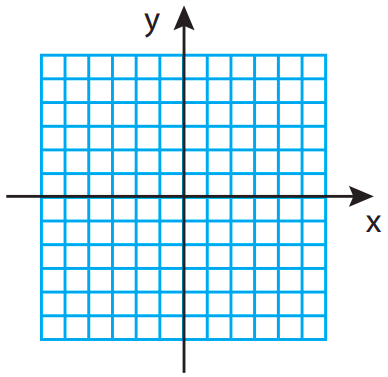
- On the grid above, draw the initial and final position vectors, and the displacement vector.
- What are the components of the displacement vector?
- What are the magnitude and direction of the displacement vector? (You can specify the direction by the angle it makes with either the positive x or the positive y axis.)
Exercise 1.6.3
Marshall Dillon is riding at 30 mph after the robber of the Dodge City bank, who has a head start of 15 minutes, but whose horse can only make 25 mph on a good day. How long does it take for Dillon to catch up with the bad guy, and how far from Dodge City are they when this happens? (Assume the road is straight, for simplicity.)
Exercise 1.6.4
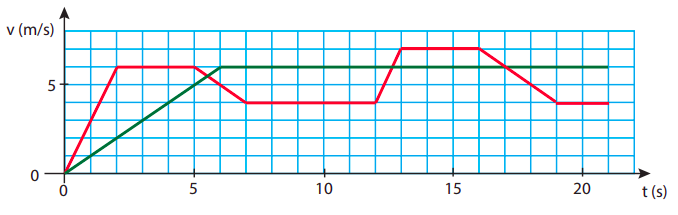
The picture below shows the velocity versus time graph of the first 21 seconds of a race between two friends, “Red” and “Green.”
- Who is ahead at t = 10 s, and by how much?
- Who passes the 100 m marker first?
Exercise 1.6.5
You are trying to pass a truck on the highway. The truck is driving at 55 mph, so you speed up to 60 mph and move over to the left lane. If the truck is 17 m long, and your car is 3 m long
- how long does it take you to pass the truck completely?
- How far (along the highway) have you traveled in that time? Note: to answer part (a) look at the problem from the perspective of the truck driver. How far are you going relative to him, and how far would it take you to cover 20 m at that speed?
Exercise 1.6.6
Suppose the position function of a particle moving in one dimension is given by
x(t)=5+3t+2t2−0.5t3
where the coefficients are such that the result will be in meters if you enter the time in seconds. What is the particle’s velocity at t = 2 s? There are two ways you can do this:
- If you know calculus, calculate the derivative of Eq (???) and evaluate it at t = 2 s.
- If you do not yet know how to take derivatives, calculate the limit in the definition (1.2.8). That is to say, calculate Δx/Δt with ti = 2 s and Δt equal, first, to 0.1 s, then to 0.01 s, and then to 0.001 s. You will need to keep more than the usual 4 decimals in the intermediate calculations if you want an accurate result, but you should still report only 3 significant digits in the final result.
Exercise 1.6.7
Suppose you are rowing across a river, as in Figure 1.3.2. Your speed is 2 miles per hour relative to the current, which is moving at a leisurely 1 mile per hour. If the river is 10 m wide,
- How far downstream do you end up?
- To row straight across you would need to have an upstream velocity component (relative to the current). How large would that be?
- If your rowing speed is still only 2 miles per hour, how long does it take you to row across the river now?


