3.3: Extended Systems and Center of Mass
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider a collection of particles with masses m1, m2,..., and located, at some given instant, at positions x1, x2 .... (We are still, for the time being, considering only motion in one dimension, but all these results generalize easily to three dimensions.) The center of mass of such a system is a mathematical point whose position coordinate is given by
Clearly, the denominator of (???) is just the total mass of the system, which we may just denote by M. If all the particles have the same mass, the center of mass will be somehow “in the middle” of all of them; otherwise, it will tend to be closer to the more massive particle(s). The “particles” in question could be spread apart, or they could literally be the “parts” into which we choose to subdivide, for computational purposes, a single extended object.
If the particles are in motion, the position of the center of mass, xcm, will in general change with time. For a solid object, where all the parts are moving together, the displacement of the center of mass will just be the same as the displacement of any part of the object. In the most general case, we will have (by subtracting xcmi from xcmf)
Δxcm=1M(m1Δx1+m2Δx2+…).
Dividing Equation (???) by Δt and taking the limit as Δt→0, we get the instantaneous velocity of the center of mass:
But this is just
where psys=m1v1+m2v2+… is the total momentum of the system.
Center of Mass Motion for an Isolated System
Equation (???) is a very interesting result. Since the total momentum of an isolated system is constant, it tells us that the center of mass of an isolated system of particles moves at constant velocity, regardless of the relative motion of the particles themselves or their possible interactions with each other. As indicated above, this generalizes straightforwardly to more than one dimension, so we can write →vcm=→psys/M. Thus, we can say that, for an isolated system in space, not only the speed, but also the direction of motion of its center of mass does not change with time.
Clearly this result is a sort of generalization of the law of inertia. For a solid, extended object, it does, in fact, provide us with the precise form that the law of inertia must take: in the absence of external forces, the center of mass will just move on a straight line with constant velocity, whereas the object itself may be moving in any way that does not affect the center of mass trajectory. Specifically, the most general motion of an isolated rigid body is a straight line motion of its center of mass at constant speed, combined with a possible rotation of the object as a whole around the center of mass.
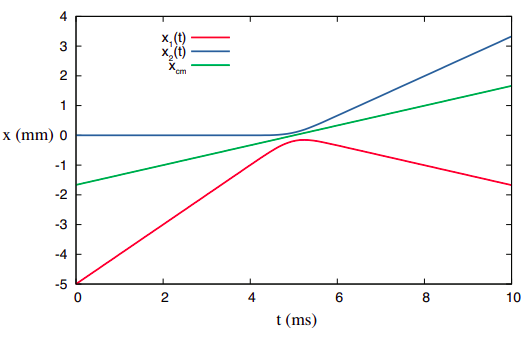
For a system that consists of separate parts, on the other hand, the center of mass is generally just a point in space, which may or may not coincide at any time with the position of any of the parts, but which will nonetheless move at constant velocity as long as the system is isolated. This is illustrated by Figure 3.3.1, where the position vs. time curves have been drawn for the colliding objects of Figure 3.1.1. I have assumed that object 1 starts out at x1i = −5 mm at t = 0, and object 2 starts at x2i = 0 at t = 0. Because object 2 has twice the inertia of object 1, the position of the center of mass, as given by Equation (???), will always be
xcm=x1/3+2x2/3
that is to say, the center of mass will always be in between objects 1 and 2, and its distance from object 2 will always be half its distance to object 1:
|xcm−x1|=23|x1−x2||xcm−x2|=13|x1−x2|
Figure 3.3.1 shows that this simple prescription does result in motion with constant velocity for the center of mass (the green straight line), even though the x-vs-t curves of the two objects themselves look relatively complicated. (Please check it out! Take a ruler to Figure 3.3.1 and verify that the center of mass is, at every instant, where it is supposed to be.)
The concept of center of mass gives us an important way to simplify the description of the motion of potentially complicated systems. We will make good use of it in forthcoming chapters.
A very nice demonstration of the motion of the center of mass in two-body one-dimensional collisions can be found at https://phet.colorado.edu/sims/collision-lab/collision-lab_en.html (you need to check the “center of mass” box to see it).
Recoil and Rocket Propulsion
As we have just seen, you cannot alter the motion of your center of mass without relying on some external force—which is to say, some kind of external support. This is actually something you may have experienced when you are resting on a very slippery surface and you just cannot “get a grip” on it. There is, however, one way to circumvent this problem which, in fact, relies on conservation of momentum itself: if you are carrying something with you, and can throw it away from you at high speed, you will recoil as a result of that. If you can keep throwing things, you (with your store of as yet unthrown things) will speed up a little more every time. This is, in essence, the principle behind rocket propulsion.
Mathematically, consider two objects, of masses m1 and m2, initially at rest, so their total momentum is zero. If mass 1 is thrown away from mass 2 with a speed v1f , then, by conservation of momentum (always assuming the system is isolated) we must have
0=m1v1f+m2v2f
and therefore v2f=−m1v1f/m2. This is how a rocket moves forward, by constantly expelling mass (the hot exhaust gas) backwards at a high velocity. Note that, even though both objects move, the center of mass of the whole system does not (in the absence of any external force), as discussed above.


