5.1: Conservative Interactions
- Page ID
- 22225
Let me summarize the physical concepts and principles we have encountered so far in our study of classical mechanics. We have “discovered” one important quantity, the inertia or inertial mass of an object, and introduced two different quantities based on that concept, the momentum \(m \vec v\) and the kinetic energy \(\frac{1}{2}mv^2\). We found that these quantities have different but equally intriguing properties. The total momentum of a system is insensitive to the interactions between the parts that make up the system, and therefore it stays constant in the absence of external influences (a more general statement of the law of inertia, the first important principle we encountered). The total kinetic energy, on the other hand, changes while any sort of interaction is taking place, but in some cases it may actually return to its original value afterwards.
In this chapter, we will continue to explore this intriguing behavior of the kinetic energy, and use it to gain some important insights into the kinds of interactions we encounter in classical physics. In the next chapter, on the other hand, we will return to the momentum perspective and use it to formally introduce the concept of force. Hence, we can say that this chapter deals with interactions from an energy point of view, whereas next chapter will deal with them from a force point of view.
In the previous chapter I suggested that what was going on in an elastic collision could be interpreted, or described (perhaps in a figurative way) more or less as follows: as the objects come together, the total kinetic energy goes down, but it is as if it was being temporarily stored away somewhere, and as the objects separate, that “stored energy” is fully recovered as kinetic energy. Whether this does happen or not in any particular collision (that is, whether the collision is elastic or not) depends, as we have seen, on the kind of interaction (“bouncy” or “sticky,” for instance) that takes place between the objects.
We are going to take the above description literally, and use the name conservative interaction for any interaction that can “store and restore” kinetic energy in this way. The “stored energy” itself—which is not actually kinetic energy while it remains stored, since it is not given by the value of \(\frac{1}{2}mv^2\) at that time—we are going to call potential energy. Thus, conservative interactions will be those that have a “potential energy” associated with them, and vice-versa.
Potential Energy
Perhaps the simplest and clearest example of the storage and recovery of kinetic energy is what happens when you throw an object straight upwards, as it rises and eventually falls back down. The object leaves your hand with some kinetic energy; as it rises it slows down, so its kinetic energy goes down, down... all the way down to zero, eventually, as it momentarily stops at the top of its rise. Then it comes down, and its kinetic energy starts to increase again, until eventually, as it comes back to your hand, it has very nearly the same kinetic energy it started out with (exactly the same, actually, if you neglect air resistance).
The interaction responsible for this change in the object’s kinetic energy is, of course, the gravitational interaction between it and the Earth, so we are going to say that the “missing” kinetic energy is temporarily stored as gravitational potential energy of the system formed by the Earth and the object.
We even have a way to describe what is going on mathematically. Recall the equation \(v^2_f − v^2_i = 2a \Delta x\) for motion under constant acceleration. Let us use \(y\) instead of \(x\), for the vertical motion; let \(a = −g\), and let \(v_f\) just be the generic velocity, \(v\), at some arbitrary height \(y\). We have
\[ v^{2}-v_{i}^{2}=-2 g\left(y-y_{i}\right) \nonumber .\]
Now multiply both sides of this equation by \(\frac{1}{2}m\):
\[ \frac{1}{2} m v^{2}-\frac{1}{2} m v_{i}^{2}=-m g\left(y-y_{i}\right) \label{eq:5.1} \]
The left-hand side of (\ref{eq:5.1}) is just the change in kinetic energy (from its initial value when the object was launched). We will interpret the right-hand side as the negative of the change in gravitational potential energy. To make this clearer, rearrange Equation (\ref{eq:5.1}) by moving all the “initial” quantities to one side:
\[ \frac{1}{2} m v^{2}+m g y=\frac{1}{2} m v_{i}^{2}+m g y_{i} \label{eq:5.2} .\]
We see, then, that the quantity \(\frac{1}{2}mv^2 + mgy\) stays constant (always equal to its initial value) as the object goes up and down. Let us define the gravitational potential energy of a system formed by the Earth and an object a height \(y\) above the Earth’s surface as the following simple function of \(y\):
\[ U^{G}(y)=m g y \label{eq:5.3} .\]
Then we see from Equation (\ref{eq:5.2}) that
\[ K + U^G = \mathrm{constant} \label{eq:5.4} .\]
This is a statement of conservation of energy under the gravitational interaction. For any interaction that has a potential energy associated with it, the quantity \(K + U\) is called the (total) mechanical energy.
Figure \(\PageIndex{1}\) shows how the kinetic and potential energies of an object thrown straight up change with time. To calculate \(K\) I have used the equation \(v = v_i − gt\) (taking \(t_i\) = 0); to calculate \(U^G = mgy\), I have used \(y = y_i + v_it − \frac{1}{2}gt^2\). I have arbitrarily assumed that the object has a mass of 1 kg and an initial velocity of 2 m/s, and it is thrown from an initial height of 0.5 m above the ground. Note how the change in potential energy exactly mirrors the change in kinetic energy (so \(\Delta U^G = −\Delta K\), as indicated by Equation (\ref{eq:5.1})), and the total mechanical energy remains equal to its initial value of 6.9 J throughout.
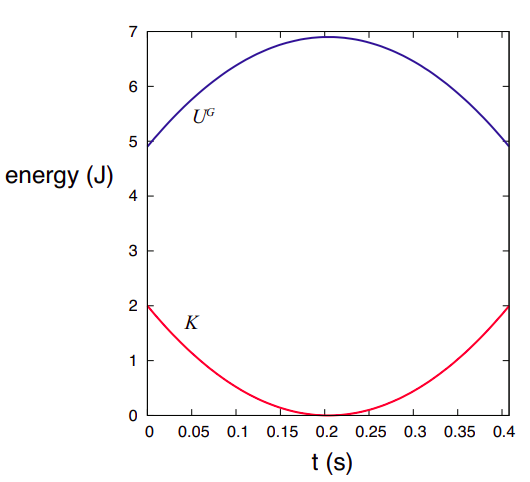
There is something about potential energy that probably needs to be mentioned at this point. Because I have chosen to launch the object from 0.5 m above the ground, and I have chosen to measure \(y\) from the ground, I started out with a potential energy of \(mgy_i\) = 4.9 J. This makes sense, in a way: it tells you that if you simply dropped the object from this height, it would have picked up an amount of kinetic energy equal to 4.9 J by the time it reached the ground. But, actually, where I choose the vertical origin of coordinates is arbitrary. I could start measuring \(y\) from any height I wanted to—for instance, taking the initial height of my hand to correspond to \(y\) = 0. This would shift the blue curve in Figure \(\PageIndex{1}\) down by 4.9 J, but it would not change any of the physics. The only important thing I really want the potential energy for is to calculate the kinetic energy the object will lose or gain as it moves from one height to another, and for that only changes in potential energy matter. I can always add or subtract any (constant) number1 to or from \(U\), and it will still be true that \(\Delta K = −\Delta U\).
What about potential energy in the context in which we first encountered it, that of elastic collisions in one dimension? Imagine that we have two carts collide on an air track, and one of them, let us say cart 2, is fitted with a spring. As the carts come together, they compress the spring, and some of their kinetic energy is “stored” in it as elastic potential energy. In physics, we use the following expression for the potential energy stored in what we call an ideal spring2:
\[ U^{\operatorname{spr}}(x)=\frac{1}{2} k\left(x-x_{0}\right)^{2} \label{eq:5.5} \]
where \(k\) is something called the spring constant; \(x_0\) is the “equilibrium length” of the spring (when it is neither compressed nor stretched); and \(x\) its actual length, so \(x>x_0\) means the spring is stretched, and \(x<x_0\) means it is compressed. For the system of the two carts colliding, we can take the potential energy to be given by Equation (\ref{eq:5.5}) if the distance between the carts is less than \(x_0\), and 0 (corresponding to a relaxed spring) otherwise. If we put cart 1 on the left and cart 2 on the right, then the distance between them is \(x_2 − x_1\), and so we can write, for the whole interaction
This is enough to solve for the motion of the two carts, given the initial conditions. To see how, look in the “Examples” section at the end of this chapter. Here, I will just give you the result.
For the calculation, shown in Figure \(\PageIndex{2}\) below, I have chosen cart 1 to have a mass of 1 kg, an initial position (at \(t\) = 0) of \(x_{1i}\) = −5 cm and an initial velocity of 1 m/s, whereas cart 2 has a mass of 2 kg and starts at rest at \(x_{2i}\) = 0. I have assumed the spring has a length of \(x_0\) = 2 cm and a spring constant \(k\) = 1000 J/m2 (which sounds like a lot but isn’t really). The collision begins at \(t_c = (x_{2i} − x_0 − x_{1i})/v_{1i}\) = 0.03 s, which is the time it takes cart 1 to travel the 3 cm separating it from the end of the spring. Prior to that point, the total kinetic energy \(K_{sys}\) = 0.5 J, and the total potential energy \(U\) = 0.
As a result of the collision, the spring compresses and undergoes “half a cycle” of oscillation with an “angular frequency” \(\omega = \sqrt{k/ \mu} \) (where \(\mu\) is, as in previous chapters, the “reduced mass” of the system, \(\mu = m_1m_2/(m_1 + m_2)\)). That is, the spring is compressed and then pushes out until it gets back to its equilibrium length3. This lasts from \(t = t_c\) until \(t = t_c + \pi / \omega\), during which time the potential and kinetic energies of the system can be written as
(don’t worry, all this will make a lot more sense after we get to Chapter 11 on simple harmonic motion, I promise!). After \(t = t_c + \pi / \omega\), the interaction is over, and \(K\) and \(U\) go back to their initial values.
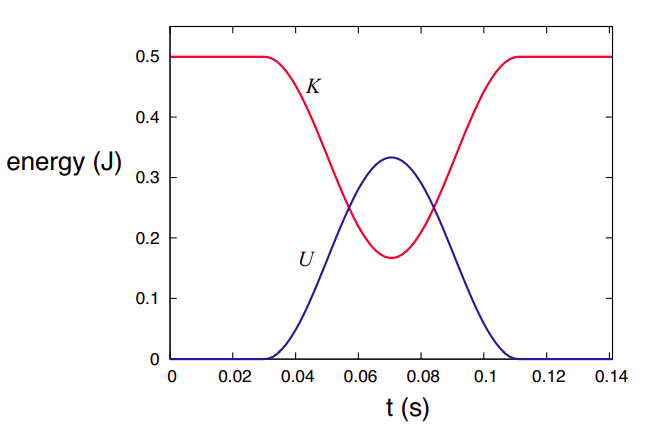
If you compare Figure \(\PageIndex{2}\) with Figure 4.2.1 of Chapter 4, you’ll see that the kinetic energy curve looks very similar, except for the time scale, which here is hundredths of a second and over there was taken to be milliseconds. The quantity that determines the time scale here is the “half period” of oscillation, \(\pi / \omega = \pi \sqrt{\mu /k}\) = 0.081 s for the values of \(k\) and \(\mu\) assumed here. We could make this smaller by making the spring stiffer (increasing \(k\)), or the blocks lighter (reducing µ), but there’s not much point in trying, since the collisions in Chapters 3 and 4 were all just made up in any case.
The main point is that this kind of physical setup (a cart fitted with a spring) would indeed give us an elastic collision, and a kinetic energy curve very much like the ones I used, for illustration purposes, in Chapter 4; only now we also have a potential energy curve to go with it, and to show where the energy is “hiding” while the collision lasts.
(You might wonder, anyway, what kind of potential energy function would actually produce the made-up elastic collision curves in Chapters 3 and 4? The (perhaps surprising) answer is, I do not really know, and I have no way to find out! If you are curious about why, again look at the “Examples” section at the end of the chapter.)
1Of course, some choices may result in the potential energy, and even the total energy, being negative sometimes! If this notion of a negative total energy bothers you a bit, wait until the chapter on gravity (Chapter 10), where we will try to make some sense out of it...
2An “ideal spring” is basically defined, mathematically, by this expression, or by the corresponding force equation (6.2.10) (which we will study in the next chapter, and which goes by the name of Hooke’s law); usually, we also require that the spring be “massless” (by which we mean that its mass should be negligible compared to all the other masses involved in any given problem). Of course, for Equation (\ref{eq:5.5}) to hold for \(x < x_0\), it must be possible to compress the spring as well as stretch it, which is not always possible with some springs.
3As noted earlier, we shall always assume our springs to be “massless,” that is, that their inertia is negligible. In turn, negligible inertia means that the spring does not “keep going”: it stops stretching as soon as it is back to its original length.
Potential Energy Functions and "Energy Landscapes"
The potential energy function of a system, as illustrated in the above examples, serves to let us know how much energy can be stored in, or extracted from, the system by changing its configuration, that is to say, the positions of its parts relative to each other. We have seen this in the case of the gravitational force (the “configuration” in this case being the distance between the object and the earth), and just now in the case of a spring (how stretched or compressed it is). In all these cases we should think of the potential energy as being a property of the system as a whole, not any individual part; it is, very loosely speaking, something akin to a “stress” in the system that can be turned into motion under the right conditions.
It is a consequence of the principle of conservation of momentum that, if the interaction between two particles can be described by a potential energy function, this should be a function only of their relative position, that is, the quantity \(x_1 − x_2\) (or \(x_2 − x_1\)), and not of the individual coordinates, \(x_1\) and \(x_2\), separately4. The example of the spring in the previous section illustrates this, whereas the gravitational potential energy example shows how this can be simplified in an important case: in Equation (\ref{eq:5.3}), the height \(y\) of the object above the ground is really a measure of the distance between the object and the earth, something that we could write, in full generality, as \(|\vec r_o − \vec r_E|\) (where \(\vec r_o\) and \(\vec r_E\) are the position vectors of the Earth and the object, respectively). However, since we do not expect the Earth to move very much as a result of the interaction, we can take its position to be constant, and only include the position of the object explicitly in our potential energy function, as we did above5.
Generally speaking, then, we can identify a large class of problems where a “small” object or “particle” interacts with a much more massive one, and it is a good approximation to write the potential energy of the whole system as a function of only the position of the particle. In one dimension, then, we have a situation where, once the initial conditions (the particle’s initial position and velocity) are known, the motion of the particle can be completely determined from the function \(U(x)\), where \(x\) is the particle’s position at any given time. This can be done using calculus (namely, let \(v=\pm \sqrt{2 m(E-U(x))}\) and solve the resulting differential equation); but it is also possible to get some pretty valuable insights into the particle’s motion without using any calculus at all, through a mostly graphical approach that I would like to show you next.
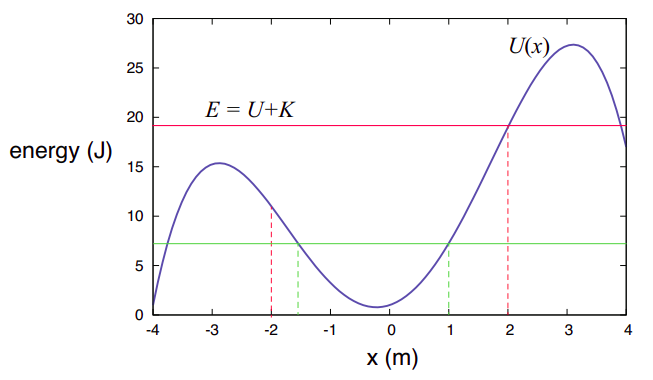
In Figure \(\PageIndex{3}\) above I have assumed, as an example, that the potential energy of the system, as a function of the position of the particle, is given by the function \(U(x) = −x^4/4+9x^2/2+2x + 1\) (in joules, if \(x\) is given in meters). Consider then what happens if the particle has a mass \(m\) = 4 kg and is found initially at \(x_i\) = −2 m, with a velocity \(v_i\) = 2 m/s. (This scenario goes with the red lines in Figure \(\PageIndex{3}\), so please ignore the green lines for the time being.) Its kinetic energy will then be \(K_i\) = 8 J, whereas the potential energy will be \(U(−2)\) = 11 J. The total mechanical energy is then \(E\) = 19 J, as indicated by the red horizontal line.
Now, as the particle moves, the total energy remains constant, so as it moves to the right, its potential energy goes down at first, and consequently its kinetic energy goes up—that is, it accelerates. At some point, however (around \(x\) = −0.22 m) the potential energy starts to go up, and so the particle starts to slow down, although it keeps going, because \(K = E − U\) is still nonzero. However, when the particle eventually reaches the point \(x\) = 2 m, the potential energy \(U(2)\) = 19 J, and the kinetic energy becomes zero.
At that point, the particle stops and turns around, just like an object thrown vertically upwards. As it moves “down the potential energy hill,” it recovers the kinetic energy it used to have, so that when it again reaches the starting point \(x\) = −2 m, its speed is again 2 m/s, but now it is moving in the opposite direction, so it just passes through and over the next “hill” (since it has enough total energy to do so), and eventually moves outside the region shown in the figure.
As another example, consider what would have happened if the particle had been released at, say, \(x\) = 1 m, but with zero velocity. (This is illustrated by the green lines in Figure \(\PageIndex{3}\).) Then the total energy would be just the potential energy \(U(1)\) = 7.25 J. The particle could not possibly move to the right, since that would require the total energy to go up. It can only move to the left, since in that direction \(U(x)\) decreases (initially, at first), and that means \(K\) can increase (recall \(K\) is always positive as long as the particle is in motion). So the particle speeds up to the left until, past the point \(x\) = −0.22 m, \(U(x)\) starts to increase again and \(K\) has to go down. Eventually, as the figure shows, we reach a point (which we can calculate to be \(x\) = −1.548 m) where \(U(x)\) is once again equal to 7.25 J. This leaves no room for any kinetic energy, so the particle has to stop and turn back. The resulting motion consists of the particle oscillating back and forth forever between \(x\) = −1.548 m and \(x\) = 1 m.
At this point, you may have noticed that the motion I have described as following from the \(U(x)\) function in Figure \(\PageIndex{3}\) resembles very much the motion of a car on a roller-coaster having the shape shown, or maybe a ball rolling up and down hills like the ones shown in the picture. In fact, the correspondence can be made exact—if we substitute sliding for rolling, since rolling motion has complications of its own. Given an arbitrary potential energy function \(U(x)\) for a particle of mass \(m\), imagine that you build a “landscape” of hills and valleys whose height \(y\) above the horizontal, for a given value of the horizontal coordinate \(x\), is given by the function \(y(x) = U(x)/mg\). (Note that \(mg\) is just a constant scaling factor that does not change the shape of the curve.) Then, for an object of mass \(m\) sliding without friction over that landscape, under the influence of gravity, the gravitational potential energy at any point \(x\) would be \(U^G(x) = mgy = U(x)\), and therefore its speed at any point will be precisely the same as that of the original particle, if it starts at the same point with the same velocity
This notion of an “energy landscape” can be extended to more than one dimension (although they are hard to visualize in three!), or generalized to deal with configuration parameters other than a single particle’s position. It can be very useful in a number of disciplines (not just physics), to predict the ways in which the configuration of a system may be likely to change.
4We will see why in the next chapter! But, if you want to peek ahead, nothing’s preventing you from reading sections 6.1 and 6.2 right now. Basically, to conserve momentum we need Equation (6.1.6) to hold, and as you can see from Equation (6.2.7), having the potential energy depend only on \(x_1 − x_2\) ensures that.
5This will change in Chapter 10, when we get to study gravity over a planetary scale.


