5.4: Conservation of Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Today, physics is pretty much founded on the belief that the energy of a closed system (defined as one that does not exchange energy with its surroundings—more on this in a minute) is always conserved: that is, internal processes and interactions will only cause energy to be “converted” from one form into another, but the total, after all the forms of energy available to the system have been carefully accounted for, will not change. This belief is based on countless experiments, on the one hand, and, on the other, on the fact that all the fundamental interactions that we are aware of do conserve a system’s total energy.
Of course, recognizing whether a system is “closed” or not depends on having first a complete catalogue of all the ways in which energy can be stored and exchanged—to make sure that there is, in fact, no exchange of energy going on with the surroundings. Note, incidentally, that a “closed” system is not necessarily the same thing as an “isolated” system: the former relates to the total energy, the latter to the total momentum. A parked car getting hotter in the sun is not a closed system (it is absorbing energy all the time) but, as far as its total momentum is concerned, it is certainly fair to call it “isolated.” (And as you keep this in mind, make sure you also do not mistake “isolated” for “insulated”!) Hopefully all these concepts will be further clarified when we introduce the additional auxiliary concepts of force, work, and heat (although the latter will not come until the end of the semester).
For a closed system, we can state the principle of conservation of energy (somewhat symbolically) in the form
where K is the total, macroscopic, kinetic energy; U the sum of all the applicable potential energies associated with the system’s internal interactions; Esource is any kind of internal energy (such as chemical energy) that is not described by a potential energy function, but can increase the system’s mechanical energy; and Ediss stands for the contents of the “dissipated energy reservoir”—typically thermal energy. As with the potential energy U, the absolute value of Esource and Ediss does not (usually) really matter: all we are interested in is how much they change in the course of the process under consideration.
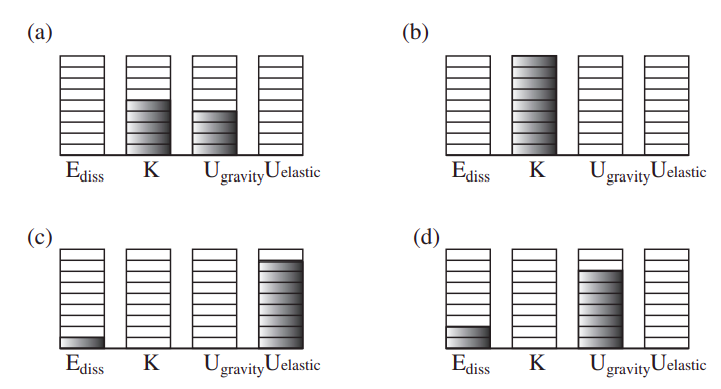
Figure 5.4.1 above is an example of this kind of “energy accounting” for a ball bouncing on the ground. If the ball is thrown down, the system formed by the ball and the earth initially has both gravitational potential energy, and kinetic energy (diagram (a)). Note that we could write the total kinetic energy as Kcm+Kconv, as we did in the previous chapter, but because of the large mass of the earth, the center of mass of the system is essentially the center of the earth, which, in our earth-bound coordinate system, does not move at all, so Kcm is, to an excellent approximation, zero. Then, the reduced mass of the system, μ=mbME/(mb+ME) is, also to an excellent approximation, just equal to the mass of the ball, so Kconv=12μv212=12mb(vb−ve)2=12mbv2b (again, because the earth does not move). So all the kinetic energy that we have is the kinetic energy of the ball, and it is all, in principle, convertible (as you can see if you replace the ball, for instance, with a bean bag).
As the ball falls, gravitational potential energy is being converted into kinetic energy, and the ball speeds up. As it is about to hit the ground (diagram (b)), the potential energy is zero and the kinetic energy is maximum. During the collision with the ground, all the kinetic energy is temporarily converted into other forms of energy, which are essentially elastic energy of deformation (like the energy in a spring) and some thermal energy (diagram (c)). When it bounces back, its kinetic energy will only be a fraction e2 of what it had before the collision (where e is the coefficient of restitution). This kinetic energy is all converted into gravitational potential energy as the ball reaches the top of its bounce (diagram (d)). Note there is more dissipated energy in diagram (d) than in (c); this is because I have assumed that dissipation of energy takes place both during the compression and the subsequent expansion of the ball.


