6.6: Examples
( \newcommand{\kernel}{\mathrm{null}\,}\)
Example 6.6.1: Dropping an object on a weighing scale
(Short version) Suppose you drop a 5-kg object on a spring scale from a height of 1 m. If the spring constant is k = 20, 000 N/m, what will the scale read?
(Long version) OK, let’s break that up into parts. Suppose that a spring scale is just a platform (of negligible mass) sitting on top of a spring. If you put an object of mass m on top of it, the spring compresses so that (in equilibrium) it exerts an upwards force that matches that of gravity.
- If the spring constant is k and the object’s mass is m and the whole system is at rest, what distance is the spring compressed?
- If you drop the object from a height h, what is the (instantaneous) maximum compression of the spring as the object is brought to a momentary rest? (This part is an energy problem! Assume that h is much greater than the actual compression of the spring, so you can neglect that when calculating the change in gravitational potential energy.)
- What mass would give you that same compression, if you were to place it gently on the scale, and wait until all the oscillations died down?
- OK, now answer the question at the top!
Solution
(a) The forces acting on the object sitting at rest on the platform are the force of gravity, FGE,o=−mg, and the normal force due to the platform, Fnp,o. This last force is equal, in magnitude, to the force exerted on the platform by the spring (it has to be, because the platform itself is being pushed down by a force Fno,p=−Fnp,o, and this has to be balanced by the spring force). This means we can, for practical purposes, pretend the platform is not there and just set the upwards force on the object equal to the spring force, Fsprs,p=−k(x−x0). So, Newton’s second law gives
Fnet=FGE,o+Fsprs,p=ma=0.
For a compressed spring, x−x0 is negative, and we can just let d=x0−x be the distance the spring is compressed. Then Equation (???) gives
−mg+kd=0
so
d=mg/k
when you just set an object on the scale and let it come to rest.
(b) This part, as the problem says, is a conservation of energy situation. The system formed by the spring, the object and the earth starts out with some gravitational potential energy, and ends up, with the object momentarily at rest, with only spring potential energy:
UGi+Uspri=UGf+Usprfmgyi+0=mgyf+12kdmax
where I have used the subscript “max” on the compression distance to distinguish it from what I calculated in part (a) (this kind of makes sense also because the scale is going to swing up and down, and we want only the maximum compression, which will give us the largest reading). The problem said to ignore the compression when calculating the change in U^G, meaning that, if we measure height from the top of the scale, y_i = h and y_f = 0. Then, solving Equation (\ref{eq:6.35}) for d_{max}, we get
d_{\max }=\sqrt{\frac{2 m g h}{k}} \label{eq:6.36} .
(c) For this part, let us rewrite Equation (\ref{eq:6.34}) as m_{eq} = kd_{max}/g, where m_{eq} is the “equivalent” mass that you would have to place on the scale (gently) to get the same reading as in part (b). Using then Equation (\ref{eq:6.36}),
m_{e q}=\frac{k}{g} \sqrt{\frac{2 m g h}{k}}=\sqrt{\frac{2 m k h}{g}} \label{eq:6.37} .
(d) Now we can substitute the values given: m = 5 kg, h = 1 m, k = 20, 000 N/m. The result is m_{eq} = 143 kg.
(Note: if you found the purely algebraic treatment above confusing, try substituting numerical values in Eqs. (\ref{eq:6.34}) and (\ref{eq:6.36}). The first equation tells you that if you just place the 5-kg mass on the scale it will compress a distance d = 2.45 mm. The second tells you that if you drop it it will compress the spring a distance d_{max} = 70 mm, about 28.6 times more, which corresponds to an “equivalent mass” 28.6 times greater than 5 kg, which is to say, 143 kg. Note also that 143 kg is an equivalent weight of 309 pounds, so if you want to try this on a bathroom scale I’d advise you to use smaller weights and drop them from a much smaller height!)
Example \PageIndex{2}: Speeding up and slowing down
- A 1400-kg car, starting from rest, accelerates to a speed of 30 mph in 10 s. What is the force on the car (assumed constant) over this period of time?
- Where does this force comes from? That is, what is the (external) object that exerts this force on the car, and what is the nature of this force?
- Draw a free-body diagram for the car. Indicate the direction of motion, and the direction of the acceleration.
- Now assume that the driver, traveling at 30 mph, sees a red light ahead and pushes on the brake pedal. Assume that the coefficient of static friction between the tires and the road is \mu_s = 0.7, and that the wheels don’t “lock”: that is to say, they continue rolling without slipping on the road as they slow down. What is the car’s minimum stopping distance?
- Draw a free-body diagram of the car for the situation in (d). Again indicate the direction of motion, and the direction of the acceleration.
- Now assume that the driver again wants to stop as in part (c), but he presses on the brakes too hard, so the wheels lock, and, moreover, the road is wet, and the coefficient of kinetic friction is only \mu_k = 0.2. What is the distance the car travels now before coming to a stop?
Solution
(a) First, let us convert 30 mph to meters per second. There are 1, 609 meters to a mile, and 3, 600 seconds to an hour, so 30 mph = 10 × 1609/3600 m/s = 13.4 m/s.
Next, for constant acceleration, we can use Equation (2.2.4): \Delta v = a \Delta t. Solving for a,
a=\frac{\Delta v}{\Delta t}=\frac{13.4 \: \mathrm{m} / \mathrm{s}}{10 \: \mathrm{s}}=1.34 \: \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber .
Finally, since F = ma, we have
F=m a=1400 \: \mathrm{kg} \times 1.34 \: \frac{\mathrm{m}}{\mathrm{s}^{2}}=1880 \: \mathrm{N} \nonumber .
(b) The force must be provided by the road, which is the only thing external to the car that is in contact with it. The force is, in fact, the force of static friction between the car and the tires. As explained in the chapter, this is a reaction force (the tires push on the road, and the road pushes back). It is static friction because the tires are not slipping relative to the road. In fact, we will see in Chapter 9 that the point of the tire in contact with the road has an instantaneous velocity of zero (see Figure 9.6.1).
(c) This is the free-body diagram. Note the force of static friction pointing forward, in the direction of the acceleration. The forces have been drawn to scale.
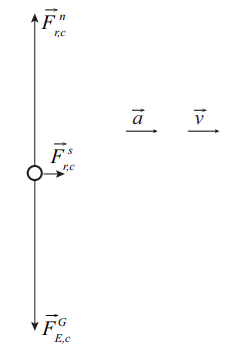
(d) This is the opposite of part (a): the driver now relies on the force of static friction to slow down the car. The shortest stopping distance will correspond to the largest (in magnitude) acceleration, as per our old friend, Equation (2.2.10):
v_{f}^{2}-v_{i}^{2}=2 a \Delta x \label{eq:6.38} .
In turn, the largest acceleration will correspond to the largest force. As explained in the chapter, the static friction force cannot exceed \mu_sF^n (Equation (6.3.8)). So, we have
F_{\max }^{s}=\mu_{s} F^{n}=\mu_{s} m g \nonumber
since, in this case, we expect the normal force to be equal to the force of gravity. Then
\left|a_{\max }\right|=\frac{F_{\max }^{s}}{m}=\frac{\mu_{s} m g}{m}=\mu_{s} g \nonumber .
We can substitute this into Equation (\ref{eq:6.38}) with a negative sign, since the acceleration acts in the opposite direction to the motion (and we are implicitly taking the direction of motion to be positive). Also note that the final velocity we want is zero, v_f = 0. We get
-v_{i}^{2}=2 a \Delta x=-2 \mu_{s} g \Delta x \nonumber .
From here, we can solve for \Delta x:
\Delta x=\frac{v_{i}^{2}}{2 \mu_{s} g}=\frac{(13.4 \: \mathrm{m} / \mathrm{s})^{2}}{2 \times 0.7 \times 9.81 \: \mathrm{m} / \mathrm{s}^{2}}=13.1 \: \mathrm{m} \nonumber .
(e) Here is the free-body diagram. The interesting feature is that the force of static friction has reversed direction relative to parts (a)–(c). It is also much larger than before. (The forces are again to scale.)
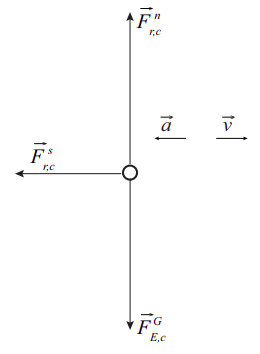
(f) The math for this part is basically identical to that in part (d). The difference, physically, is that now you are dealing with the force of kinetic (or “sliding”) friction, and that is always given by F^k = \mu_kF^n (this is not an upper limit, it’s just what F^k is). So we have a = −F^k/m = −mu_kg, and, just as before (but with \mu_k replacing \mu_s),
\Delta x=\frac{v_{i}^{2}}{2 \mu_{k} g}=\frac{(13.4 \: \mathrm{m} / \mathrm{s})^{2}}{2 \times 0.2 \times 9.81 \: \mathrm{m} / \mathrm{s}^{2}}=45.8 \: \mathrm{m} \nonumber .
This is a huge distance, close to half a football field! If these numbers are accurate, you can see that locking your brakes in the rain can have some pretty bad consequences.


