8.8: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 8.8.1
A pitcher throws a fastball horizontally at a speed of 42 m/s. Neglecting air resistance,
- How long does it take for the ball to reach the batter, a distance of 18.4 m away?
- How much does the ball drop vertically in this time?
- What is the vertical component of the ball’s velocity as it reaches the batter?
(Just to set the record straight, a real fastball would probably not drop that much, because of a lift force, called the Magnus effect, due to the interaction of the air with the backspin of the ball!)
Exercise 8.8.2
Two blocks are connected by a massless string threaded over a massless, frictionless pulley, as shown in the picture. The mass of block 1 is 2 kg and the mass of block 2 is 1.5 kg. The angle of the incline is 30∘. There is friction between the block and the inclined surface.
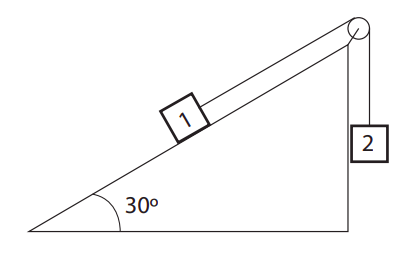
- Start by assuming that the coefficient of static friction is strong enough to keep the system from moving, and draw free-body diagrams for the two blocks. Try to get all the forces approximately to scale. (The following questions may be helpful.)
- If the system is not moving, what is the magnitude of the tension?
- What is the magnitude of the normal force?
- How large does the coefficient of static friction have to be to keep the system from moving?
- Now suppose the system is moving, and the coefficient of sliding (kinetic) friction is 0.2. What is the acceleration of the system?
- What is the tension now?
- What is the rate at which energy is dissipated (instantaneous dissipated power) when the system’s velocity is 3 m/s?
Exercise 8.8.3
A 60-kg skier starts sliding from rest from the top of a slope that makes an angle of 30∘ with the horizontal. Assume the bottom of the slope is 100 m below the top (measured vertically).
- What is the change in the gravitational potential energy of the system formed by the skier and the Earth, as the skier slides from the top to the bottom of the slope?
- What is the work done by gravity on the skier for the process described above? (Thinking now of the skier only as the system.)
- If you could neglect the friction between the skis and the snow, what would be the speed of the skier at the bottom of the slope? Why?
- If the speed of the skier is only 30 m/s as she reaches the bottom of the slope, how much energy was dissipated by friction?
- Draw a free-body diagram of the skier as she is sliding down the slope. Make sure you include friction, and indicate the direction of the acceleration. Use your diagram to answer the next couple of questions.
- What is the magnitude of the normal force exerted by the ground on the skier?
- Under the same assumptions as in part (d) above, what is the coefficient of friction between the skis and the snow?
- Again under the assumption that her final speed is 30 m/s, what is the acceleration of the skier along the slope?
Exercise 8.8.4
A child is dragging a 2 kg sled through a flat patch of snow (coefficient of kinetic friction: 0.1) with a constant force, by pulling on a rope at an angle of 25∘ to the horizontal. The sled is moving at a constant speed.
- Draw a free body diagram for the sled as it is being pulled.
- Find the magnitude of all the forces acting on the sled.
- If the child were to suddenly release the rope, what would be the new value of the friction force? What would be the sled’s acceleration? (Take the initial direction of motion to be positive.)
Exercise 8.8.5
A man is swinging an object, attached to a string, in a circle over his head (see the sketches).
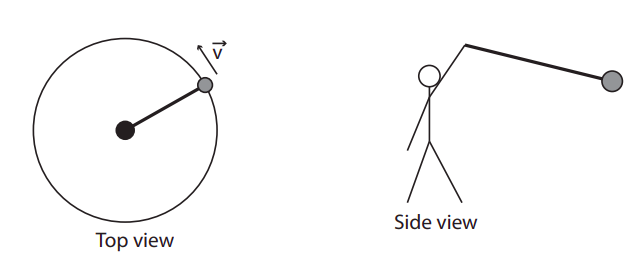
- Draw a free-body diagram for the object. Notice the string is not drawn horizontal in the “side view” diagram above. Why is that?
- If the mass of the object is 1 kg, what is the vertical component of the tension?
- If the object makes 3 turns per second, and the radius of the circle (as seen in the top view) is 0.8 m, what is the centripetal acceleration of the object?
- Which force component in your diagram provides this centripetal acceleration?
- Based on your results above, what is the angle the string must make with the horizontal?
Exercise 8.8.6
A golf ball is hit in such a way that it travels 300 m horizontally and stays in the air a total of 6 s. What was its initial velocity? (give horizontal and vertical components, and also magnitude and direction).
Exercise 8.8.7
A 2 kg block is initially at rest at the top of a 35∘ incline, and is then allowed to slide down the incline. The coefficient of kinetic friction is μk = 0.25.
- Draw a free-body diagram for the block.
- Find the components of the gravitational force in the given coordinate system.
- Find the normal force and the force of kinetic friction.
- Find the magnitude of the acceleration of the block.
- What is the final speed of the block after sliding 0.75 m?
- If the coefficient of static friction is μs = 0.4, what would the maximum value of the angle θ be for the block to not slide when it is released?
Exercise 8.8.8
You throw a ball for your dog to fetch. The ball leaves your hand with a speed of 2 m/s, at an angle of 30∘ to the horizontal, and from a height of 1.5 m above the ground. The mass of the ball is 0.5 kg. Neglect air resistance in what follows.
- What is the acceleration of the ball while it is in flight? Report it as a vector, that is, specify magnitude and direction (or vertical and horizontal components; if the latter, specify which direction(s) you take as positive).
- What is the kinetic energy of the ball as it leaves your hand?
- Consider the Earth as being in the system. What is the potential energy of the Earth-ball system (1) as the ball leaves your hand, (2) at its maximum height, and (3) as it finally hits the ground?
- How high does the ball rise above the ground?
- What is the kinetic energy of the ball as it hits the ground?
- Now let the system be the ball alone. How much work does the Earth do on the ball while it is in flight? (from start to finish)
- What is the velocity of the ball as it hits the ground? Report it as a vector.
- How far away from you (horizontally) does the ball land?
Exercise 8.8.9
A man is standing on the platform of a merry-go-round, not holding on to anything. The merry-go-round is turning at a constant rate, and makes a complete turn every 10 s.
- What is the merry-go-round’s angular velocity?
- If the man is standing at a distance of 2 m from the center of the merry-go-round, what is his centripetal acceleration?
- Which actual force acting on the man is responsible for this acceleration?
- What is the minimum value of μs, the static friction coefficient, between the soles of the man’s shoes and the platform?
- The power is turned off and the platform slows down to a stop with a constant angular acceleration of −0.02 rad/s2. How long does it take for it to stop completely?
- What is the man’s tangential acceleration during that time? Does his centripetal acceleration change? Why?
- How many turns does the platform make before coming to a complete stop?


