8.7: Advanced Topics
- Page ID
- 22407
Example \(\PageIndex{1}\): Staying on track
(This example studies a situation that you could easily setup experimentally at home (you can use a whole sphere instead of a half-sphere!), although to get the numbers to work out you really need to make sure that the friction between the surface and the object you choose is truly negligible. Essentially the same mathematical approach could be used to study the problem of a skier going over a mogul, or a car losing contact with the road if it is going too fast over a hill.)
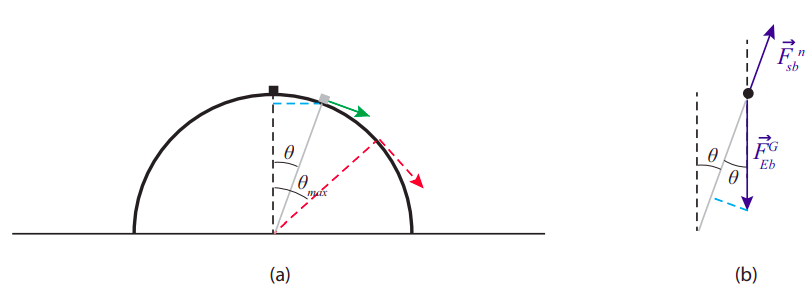
A small object is placed at the top of a smooth (frictionless) dome shaped like a half-sphere of radius \(R\), and given a small push so it starts sliding down the dome, initially moving very slowly \(\left(v_{i} \simeq 0\right)\), but picking up speed as it goes, until at some point it flies off the surface.
- At that point, when the object loses contact with the surface, what is the angle that its position vector (with origin at the center of the sphere) makes with the vertical?
- How far away from the sphere does the object land?
Solution
(a) As we saw in Section 8.4, in order to get an object to move along an arc of a circle, a centripetal force of magnitude \(mv^2/r\) is required. As long as our object is in contact with the surface, the forces acting on it are the normal force (which points along the radial direction, so it makes a negative contribution to the centrifugal force) and gravity, which has a component \(mg \cos \theta\) along the radius, towards the center of the circle (see Figure \(\PageIndex{1}\)(b), the dashed light blue line). So, the centripetal force equation reads
\[ \frac{m v^{2}}{R}=m g \cos \theta-F^{n} \label{eq:8.46} .\]
The next thing we need to do is find the value of the speed v for a given angle \(\theta\). If we treat the object as a particle, its only energy is kinetic energy, and \(\Delta K = W_{net}\) (Equation (7.2.8)), where \(W_{net}\) is the work done on the particle by the net force acting on it. The normal force is always perpendicular to the displacement, so it does no work, whereas gravity is always vertical and does work \(W_{grav} = −mg\Delta y\) (taking upwards as positive, so \(\Delta y\) is negative). In fact, from Figure \(\PageIndex{1}\)(a) (follow the dashed blue line) you can see that for a given angle \(\theta\), the height of the object above the ground is \(R \cos \theta\), so the vertical displacement from its initial position is
\[ \Delta y=-(R-R \cos \theta) \label{eq:8.47} \]
Hence we have, for the change in kinetic energy,
\[ \frac{1}{2} m v^{2}-\frac{1}{2} m v_{i}^{2}=m g R-m g R \cos \theta \label{eq:8.48} .\]
Assuming, as we are told in the text of the problem, that \(v_{i} \simeq 0\), we get \(v^2 \simeq 2gR − 2gR \cos \theta \), and using this in Equation (\ref{eq:8.46})
\[ 2 m g-2 m g \cos \theta=m g \cos \theta-F^{n} \label{eq:8.49} \]
or \(F^n = 3mg \cos \theta −2mg\). This shows that \(F^n\) starts out (when \(\theta\) = 0) having its usual value of \(mg\), and then it becomes progressively smaller as the object slides down. The point where the object loses contact with the surface is when \(F^n\) = 0, and that happens for
\[ 3 \cos \theta_{max} = 2 \label{eq:8.50} \]
or \(\theta_{\max }=\cos ^{-1}(2 / 3)=48.2^{\circ} \).
Recalling that \(\Delta y = −(R − R \cos \theta)\), we see that when \( \cos \theta\) = 2/3, the object has fallen a distance \(R\)/3; put otherwise, its height above the ground at the time it flies off is 2\(R\)/3, or 2/3 of the initial height.
(b) This is just a projectile problem now. We just have to find the values of the initial conditions (\(x_i\), \(y_i\), \(v_{x,i}\) and \(v_{y,i}\)) and substitute in the equations (8.2.2). By inspecting the figure, you can see that, at the time the object flies off,
\begin{align}
&x_{i}=R \sin \theta_{\max }=0.745 R \nonumber \\
&y_{i}=R \cos \theta_{\max }=0.667 R \label{e:8.51}.
\end{align}
Also, we found above that \(v^{2} \simeq 2 g R-2 g R \cos \theta\), and when \(\theta = \theta_{max}\) this gives \(v^2 = 0.667gR\), or \(v=0.816 \sqrt{g R} \). The projection angle in this case is \(−\theta_{max}\); that is, the initial velocity of the projectile (dashed red arrow in Figure \(\PageIndex{1}\)(a)) is at an angle 48.2\(^{\circ}\) below the positive \(x\) axis, so we have:
\begin{align}
&v_{x, i}=v_{i} \cos \theta_{\max }=0.544 \sqrt{g R} \nonumber \\
&v_{y, i}=-v_{i} \sin \theta_{\max }=-0.609 \sqrt{g R} \label{eq:8.52}
\end{align}
Now we just use these results in Eqs. (8.2.2). Specifically, we want to know how long it takes for the object to reach the ground, so we use the last equation (8.2.2) with \(y\) = 0 and solve for \(t\):
\[ 0=y_{i}+v_{y, i} t-\frac{1}{2} g t^{2} \label{eq:8.53} \]
The result is \(t=0.697 \sqrt{R / g}\). (You do not need to carry the “\(g\)” throughout; it would be OK to substitute 9.8 m/s2 for it. I have just kept it in symbolic form so far to make it clear that the quantities we derive will have the right units.) Substituting this in the equation for \(x\), we get
\[ x=x_{i}+v_{x, i} t=0.745 R+0.544 \sqrt{g R} \times 0.697 \sqrt{R / g}=1.125 R \label{eq:8.54} \]
(Note how the \(g\) cancels, so we would get the same result on any planet!) Since the sphere has a radius \(R\), the object falls a distance \(0.125R\) away from the sphere.
Example \(\PageIndex{2}\): Going around a banked curve
Roadway engineers often bank a curve, especially if it is a very tight turn, so the cars will not have to rely on friction alone to provide the required centripetal force. The picture shows a car going around such a curve, which we can model as an arc of a circle of radius \(r\). In terms of \(r\), the bank angle \(\theta\), and the coefficient of static friction, find the maximum safe speed around the curve.
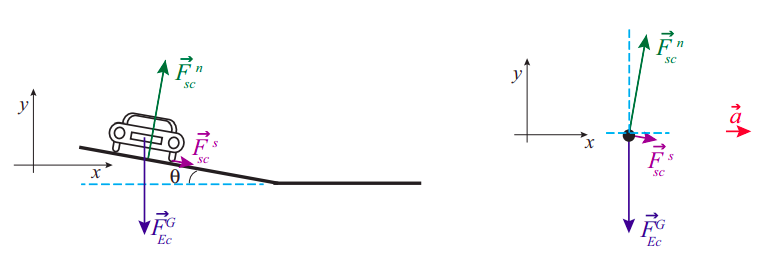
The figure shows the appropriate choice of axes for this problem. The criterion is, again, to choose the axes so that one of them will coincide with the direction of the acceleration. In this case, the acceleration is all centripetal, that is to say, pointing, horizontally, towards the center of the circle on which the car is traveling.
It may seem strange to see the force of static friction pointing down the slope, but recall that for a car turning on a flat surface it would have been pointing inwards (towards the center of the circle), so this is the natural extension of that. In general, you should always try to imagine which way the object would slide if friction disappeared altogether: \(\vec F^s\) must point in the direction opposite that. Thus, for a car traveling at a reasonable speed, the direction in which it would skid is up the slope, and that means \(\vec F^s\) must point down the slope. But, for a car just sitting still on the tilted road, \(\vec F^s\) must point upwards, and we shall see in a moment that in general there is a minimum velocity required for the force of static friction to point in the direction we have chosen.
Apart from this, the main difference with the flat surface case is that now the normal force has a component along the direction of the acceleration, so it helps to keep the car moving in a circle. On the other hand, note that we now lose (for centripetal purposes) a little bit of the friction force, since it is pointing slightly downwards. This, however, is more than compensated for by the fact that the normal force is greater now than it would be for a flat surface, since the car is now, so to speak, “driving into” the road somewhat.
The dashed blue lines in the free-body diagram are meant to indicate that the angle \(\theta\) of the bank is also the angle between the normal force and the positive \(y\) axis, as well as the angle that \(\vec F^s\) makes below the positive \(x\) axis. It follows that the components of these two forces along the axes shown are:
\begin{align}
&F_{x}^{n}=F^{n} \sin \theta \nonumber \\
&F_{y}^{n}=F^{n} \cos \theta \label{eq:8.55}
\end{align}
and
\begin{align}
&F_{x}^{s}=F^{s} \cos \theta \nonumber \\
&F_{y}^{n}=-F^{s} \sin \theta \label{eq:8.56}
\end{align}
The vertical force equation is then:
\[ 0=m a_{y}=F_{y}^{n}+F_{y}^{s}-F^{G}=F^{n} \cos \theta-F^{s} \sin \theta-m g \label{eq:8.57} .\]
This shows that \(F^n = (mg + F^s \sin \theta)/ \cos \theta \) is indeed greater than just \(mg\) for this problem, and must increase as the angle \(\theta\) increases (since \(\cos \theta\) decreases with increasing \(\theta\)). The horizontal equation is:
\[ m a_{x}=F_{x}^{n}+F_{x}^{s}=F^{n} \sin \theta+F^{s} \cos \theta=\frac{m v^{2}}{r} \label{eq:8.58} \]
where I have already substituted the value of the centripetal acceleration for \(a_x\). Equations (\ref{eq:8.57}) and (\ref{eq:8.58}) form a system that needs to be solved for the two unknowns \(F^n\) and \(F^s\). The result is:
\begin{align}
&F^{n}=m g \cos \theta+\frac{m v^{2}}{r} \sin \theta \nonumber \\
&F^{s}=-m g \sin \theta+\frac{m v^{2}}{r} \cos \theta \label{eq:8.59}.
\end{align}
Note that the second equation would have \(F^s\) becoming negative if \( v^{2}<g r \tan \theta \). This means that below that speed, the force of static friction must actually point up the slope, as discussed above. We can call this particular speed, for which \(F^s\) becomes zero, \(v_{no \: friction}\):
\[ v_{\text {no friction }}=\sqrt{g r \tan \theta} \label{eq:8.60} .\]
What this means is that it is possible to arrange the banking angle so that a car going at a specific speed would not have to rely on friction at all in order to make the curve: the normal force would be just right to provide the required centripetal acceleration. A car going at that speed would not feel either pulled down or pushed up the slope. However, a car going faster than that would tend to “fly off”, and the static friction force would be required to pull it in and keep it on the curve, whereas a car moving more slowly would tend to slide down and would have to be pushed up by the friction force. Friction, therefore, provides a range of safe speeds to drive in this case, just as it did in the flat surface case.
We can calculate the maximum safe speed as we did before, recalling that we must always have \(F^{s} \leq \mu_{s} F^{n}\). Substituting Eqs. (\ref{eq:8.59}) in this expression, and solving for \(v\), we get the condition
\[ v_{\max }=\sqrt{g r} \sqrt{\frac{\mu_{s}+\tan \theta}{1-\mu_{s} \tan \theta}} \label{eq:8.61} .\]
This reproduces our result (8.4.5) for \(\theta\) = 0 (a flat road), as it should.
To put some numbers into this, suppose the curve has a radius of 20 m, and the coefficient of static friction between the tires and the road is \(\mu_s\) = 0.7. Then, for a flat surface, we get \(v_{max}\) = 11.7 m/s, or about 26 mph, whereas for a bank angle of \(\theta\) = 10\(^{\circ}\) (the angle chosen for the figure above) we get \(v_{max}\) = 14 m/s, or about 31 mph.
Equation (\ref{eq:8.61}) actually indicates that the maximum velocity would “become infinite” for a finite bank angle, namely, if \(1 − \mu_s \tan \theta = 0\), or \(\tan \theta = 1/ \mu_s\) (if \(\mu_s\) = 0.7, this corresponds to \(\theta\) = 55\(^{\circ}\)). This is mathematically correct, but of course we cannot take it literally: it assumes that there is no limit to how large a normal force the roadway may exert without sustaining damage, and also that \(F^s\) can become arbitrarily large as long as it stays below the bound \(F^{s} \leq \mu_{s} F^{n} \). Neither of these assumptions would hold in real life for very large speeds. Also, the angle \(\theta=\tan ^{-1}\left(1 / \mu_{s}\right) \) is much too steep: recall that, according to Equation (8.3.11), the force of friction will only be able to keep an object (initially at rest) from sliding down the slope if \(\tan \theta \leq \mu_{s}\), which for \(\mu_s\) = 0.7 means \(\theta \leq 35^{\circ}\). So, with a bank angle of 55\(^{\circ}\) you might drive on the curve, provided you were going fast enough, but you could not park on it—the car would slide down! Bottom line, use Equation (\ref{eq:8.61}) only for moderate values of \(\theta\)... and do not exceed \(\theta=\tan ^{-1} \mu_{s}\) if you want a car to be able to drive around the curve slowly without sliding down into the ditch.
Example \(\PageIndex{3}\): Rotating frames of reference- centrifugal force and coriolis force
Imagine you are inside a rotating cylindrical room of radius \(R\). There is a metal puck on the floor, a distance \(r\) from the axis of rotation, held in place with an electromagnet. At some time you switch off the electromagnet and the puck is free to slide without friction. Find where the puck strikes the wall, and show that, if it was not too far away from the wall to begin with, it appears as if it had moved straight for the wall as soon as it was released.
Solution
The picture looks as shown below, to an observer in an inertial frame, looking down. The puck starts at point A, with instantaneous velocity \(\omega r\) pointing straight to the left at the moment it is released, so it just moves straight (in the inertial frame) until it hits the wall at point B. From the cyan-colored triangle shown, we can see that it travels a distance \(\sqrt{R^{2}-r^{2}}\), which takes a time
\[ \Delta t=\frac{\sqrt{R^{2}-r^{2}}}{\omega r} \label{eq:8.62} .\]
In this time, the room rotates counterclockwise through an angle \(\Delta \theta_{room} = \omega \Delta t\):
\[ \Delta \theta_{\text {room}}=\frac{\sqrt{R^{2}-r^{2}}}{r} \label{eq:8.63} .\]
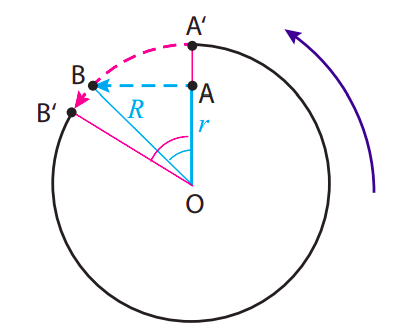
This is the angle shown in magenta in the figure. As a result of this rotation, the point A\(^{\prime}\) that was initially on the wall straight across from the puck has moved (following the magenta dashed line) to the position B\(^{\prime}\), so to an observer in the rotating room, looking at things from the point O, the puck appears to head for the wall and drift a little to the right while doing so.
The cyan angle in the picture, which we could call \(\Delta \theta_{part}\), has tangent equal to \(\sqrt{R^{2}-r^{2}} / r\), so we have
\[ \Delta \theta_{\text {room}}=\tan \left(\Delta \theta_{\text {part}}\right) \label{eq:8.64} .\]
This tells us the two angles are going to be pretty close if they are small enough, which is what happens if the puck starts close enough to the wall in the first place. The picture shows, for clarity, the case when \(r = 0.7R\), which gives \(\Delta \theta_{room}\) = 1.02 rad, and \(\Delta \theta_{part} = \tan^{−1}(1.02)\) = 0.8 rad. For \(r = 0.9R\), on the other hand, one finds \(\Delta \theta_{room}\) = 0.48 rad, and \(\Delta \theta_{part} = \tan^{−1}\)(0.48) = 0.45 rad.
In terms of pseudoforces (forces that do not, physically, exist, but may be introduced to describe mathematically the motion of objects in non-inertial frames of reference), the non-inertial observer would say that the puck heads towards the wall because of a centrifugal force (that is, a force pointing away from the center of rotation), and while doing so it drifts to the right because of the so-called Coriolis force.


