10.2: Weight, Acceleration, and the Equivalence Principle
( \newcommand{\kernel}{\mathrm{null}\,}\)
Whether we write it as mg or as GMm/r2, the force of gravity on an object of mass m has the remarkable property—not shared by any other known force—of being proportional to the inertial mass of the object. This means that, if gravity is the only force acting on a system made up of many particles, when you divide the force on each particle by the particle’s mass in order to find the particle’s acceleration, you get the same value of a for every particle (at least, assuming that they are all at about the same distance from the object exerting the force in the first place). Thus, all the parts making up the object will accelerate together, as a whole.
Suppose that you are holding an object, while in free fall (remember that “free fall” means that gravity is the only force acting on you), and you let go of it, as in Figure 10.2.1 below. Since gravity will give you and the object the same acceleration, you’ll find that it does not “fall” relative to you—that is, it will not fall any faster nor more slowly than yourself. From your own reference frame, you will just see it hovering motionless in front of you, in the same position (relative to you) that it occupied before you let go of it. This is exactly what you see in videos shot aboard the International Space Station. The result is an impression of weightlessness, or “zero gravity”—even though gravity is very much nonzero; the space station, and everything inside it, is constantly “falling” to the earth, it just does not hit it because it has some sideways velocity (or angular momentum) to begin with, and the earth’s pull just bends its trajectory around enough to keep it moving in a circle. But gravity is the only force acting on it, and on everything in it (at least until somebody pushes himself against a wall, or something like that).
So, the kind of acceleration you get from gravity is, paradoxically, such that, if you give in to it completely, you feel like there is no gravity.
The familiar sensation of weight, on the other hand, comes precisely from not giving in, and rather, enlisting other forces to fight against gravity. When you do this—when you simply stand on the surface of the earth, for instance—your feet are supported by the ground below you, but every other part of your body is supported by some other part of your body, immediately above or below it, that you can think of as a sort of spring that is either somewhat stretched or somewhat compressed. It is primarily your skeleton, and mostly your spine, that bears most of the compressive load. (See Figure 10.9, next page.) The sensation of weight is your response to this load. Interestingly, even though this constant squishing may actually result in your losing a little height in the course of a day (which you recover at night, when you lie horizontally), it is not a bad thing, rather the contrary: your bones have evolved so that they need this constant pressure to grow and replace the mass that they would otherwise lose in a “weightless” environment.
On the other hand, as shown in Figure 10.2.2(c), the same compression (or extension—for instance, for the muscles in your arms, as they hang by your side) would result from a situation in which you were, say, standing motionless inside a rocket that is accelerating upwards with a=g, but very far away from any gravity source. In Figure 10.2.2(b), the “spring” that represents your skeleton needs to be compressed so it can exert an upward force Fspr=mug to support the weight of your upper body (simplified here as just a single mass mu). In Figure 10.2.2(c), it needs to be compressed by the same amount, so it can exert the upward force Fspr=mua needed to give your upper body an acceleration a=g. The equality of the two expressions is a direct consequence of the fact that the force of gravity is proportional to an object’s inertial mass (since the second expression is just Newton's second law).
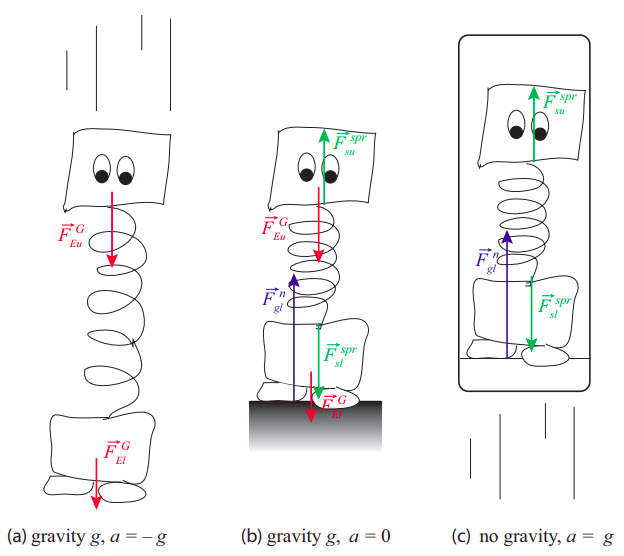
In general, then, when your whole body is subjected to an upward acceleration a, it feels like your weight is increased by an amount ma. The same thing holds regardless of direction—a forward acceleration a on a jet pilot’s body feels like a “weight” ma pushing her against her seat. This is why these “effective forces” (or, more precisely, the accelerations that cause them) are measured in g’s: a “force” of, say, 5g, means that the pilot feels pushed against her seat with a “force” equal to 5 times her weight. What’s really happening, of course, is the opposite—her seat is pushing her forward, but her internal organs are being compressed (in order to provide that same forward acceleration) the way they would under a gravity force five times stronger than at the earth’s surface.
The parallels between being in a constantly accelerating frame of reference and being at rest under the influence of a constant gravity force go beyond the subjective sensation of weight. Figure 10.2.3 illustrates what happens when you drop something while traveling in the upwardly accelerating rocket, in the absence of gravity. From an inertial observer’s point of view, the object you drop merely keeps the upward velocity it had the moment it left your hand; but, since you are in contact with the rocket, your own velocity is constantly increasing, and as a result of that you see the object fall—relative to you.
From a practical point of view, this suggests a couple of ways to provide an “artificial gravity” for astronauts who might one day have to spend a long time in space, either under extremely weak gravity (for instance, during a trip to Mars), or, what amounts to essentially the same thing, in free fall (as in a space station orbiting a planet). The one most often seen in movies consists in having the space station (or spaceship) constantly spin around an axis with some angular velocity ω. Then any object that is moving with the station, a distance R away from the axis, will experience a centripetal acceleration of magnitude ω2R, which will feel like a gravity force mω2R directed in the opposite direction, that is to say, away from the center. People would then basically “walk on the walls” (that is to say, sideways as seen from above, with their feet away from the rotation axis and their heads towards the rotation axis). If somebody let go of something they were holding, the object would “fall towards the wall.” Unfortunately, while the idea might work for a space station, it would probably be impractical for a spaceship, since one would need a fairly large R and/or a fairly large rotation rate to get ω2R≃g. (On the other hand, probably even something like 15g is better than nothing, so who knows...)
On a fundamental level, the equivalence between a constantly accelerated reference frame, and an inertial frame with a uniform gravitational field (such as, approximately, the surface of the earth), was elevated by Einstein to a basic principle of physics, which became the foundation of his general theory of relativity. This equivalence principle asserts that it is absolutely impossible to distinguish, by any kind of physics experiment, between the two situations just mentioned: a constantly accelerated reference frame is postulated to be completely equivalent in every way to an inertial frame with a uniform gravitational field.
A remarkable consequence of the equivalence principle is that light, despite having technically “zero rest mass,” must bend its trajectory under the influence of gravity. This can be seen as follows. Imagine shooting a projectile horizontally inside the rocket in Figure 10.2.3. Although an inertial observer, looking from the outside, would see the projectile travel in a straight line, the observer inside the rocket would see its path bend down, just as for the projectiles we studied back in Chapter 8. This is for the same reason he would see the object fall, relative to him, in Figure 10.2.3: the projectile has a constant velocity, so it travels the same distance in every equal time interval, but the rocket is accelerating, so the distance it travels in equal time intervals is constantly increasing. In basically the same way, then, a beam of light sent horizontally inside the rocket, and traveling with constant velocity (and, therefore, in a straight line) in an inertial frame, would be seen as bending down in the rocket’s reference frame.
However, if the equivalence principle is true, and physical phenomena look the same in a constantly accelerating frame as in an inertial frame with a constant gravitational field, it follows that light must also bend its path in the latter system, in much the same way as a projectile would. (I say “much the same way” because the effect is not just as simple as giving light an “effective mass”; there are other relativistic effects, such as space contraction and time dilation, that must also be reckoned with.) This gravitational bending was one of the most important early predictions of Einstein’s General Relativity theory, and certainly the most spectacular. Since one needs the light rays to pass vary close to a large mass to get an observable effect, the way the prediction was verified was by looking at the apparent position of the stars that can be seen close to the edge of the sun’s disk during a solar eclipse. The slight (apparent) shift in position predicted by Einstein was observed by Sir Arthur Eddington during the solar eclipse of 1919 (two expeditions were sent to remote corners of the earth for this purpose), and it was primarily responsible for Einstein’s sudden fame among the general public of his day.
Today, with modern telescopes, this so-called “gravitational lensing” effect has become an important tool in astronomy, allowing us to interpret the pictures taken of distant galaxies, which are often shifted and/or distorted by the gravity of the galaxies that lie in between them and us.
It has even become possible to imagine an object so dense that it would “capture” light, attracting it so strongly that it could not leave the object’s neighborhood. Such an object has come to be called a black hole. If you set the escape velocity of Equation (10.1.15) equal to the speed of light in vacuum, c, and solve for ri, you obtain what is called the Schwarzschild radius, rs, for a black hole of mass M; the idea being that, in order to be a black hole, the object has to be so dense that all its mass M is inside a sphere of radius smaller than rs. Physicists today believe in the existence (and even what one might call the ubiquity) of black holes, of which the Schwarzschild solution was only the first calculated example. Note that rs does not define the actual, physical surface of the object; it does, however, locate what is known as the black hole’s event horizon. Nothing can be known, through observation, about anything that might happen closer to the black hole’s center than the distance rs, since no information can be transmitted faster than light, and no light can escape from a distance ri < rs.


